31 Fórmulas Matemáticas de ACT Que necesita Conocer

Geometría plana

Ángulos y líneas

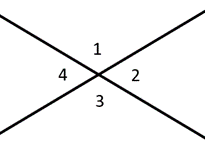
Los ángulos a lo largo de una recta se llaman ángulos suplementarios, sumando \(180^{\circ}\). Los ángulos complementarios suman \(90^{\circ}\), un ángulo recto. Los ángulos verticales describen ángulos directamente uno frente al otro, que siempre son congruentes. En el diagrama de la izquierda, por ejemplo, diríamos que los ángulos 1 & 2 son suplementarios, mientras que los ángulos 1 & 3 son ángulos verticales.

Área de un triángulo

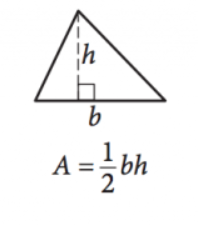
Imagen cortesía de SAT

\(\frac{1}{2}bh=A\)

Esta ecuación proporciona el área \((A)\) de cualquier triángulo dada la longitud de la base \((b)\) y la altura \((h)\). Tenga en cuenta que la altura es la longitud de la línea que se extiende en un ángulo complementario desde cualquier lado (la base) hasta el punto/ángulo directamente al otro lado de ese lado.

Para triángulos equiláteros, donde los tres lados \(s)\) tienen la misma longitud, la ecuación de área es:

\(\frac{s^2\sqrt{3}}{4}=A\)

Teorema de Pitágoras

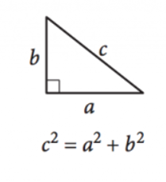
Imagen cortesía de SAT

Como los ángulos en un triángulo siempre suman \(180^{\circ}\), un triángulo rectángulo se define como cualquier triángulo con un ángulo recto, asegurando que los otros dos ángulos sean complementarios. Las longitudes laterales de los triángulos rectangulares se pueden definir por el Teorema de Pitágoras:

\(a^2+b^2=c^2\)

Aquí, \(a\) y \(b\) es la longitud de las piernas o en los lados a través de los ángulos complementarios, y \(c\) es la longitud de la hipotenusa, el lado del ángulo recto.

Puede ser útil memorizar también los siguientes triples pitagóricos,o valores para longitudes de lado \((a, b, c)\): 3-4-5, 5-12-13, 7-24-25, y 8-15-17. Tenga en cuenta que la hipotenusa es siempre el lado más largo.

Triángulos rectangulares especiales

Hay dos tipos de triángulos rectangulares especiales, que tienen los ángulos y las relaciones de longitud de la siguiente manera:

Imagen cortesía de SAT

Áreas de Cuadriláteros

\(A = lw\)

Esta fórmula proporciona el área de un rectángulo con longitud \(l\) y anchura \(w\).

\(A = bh\)

Esta fórmula proporciona el área de un paralelogramo dada la base \(b\) , la longitud de los lados más largos y la altura \(h\), definida como la longitud de la línea que se extiende en un ángulo complementario hacia arriba de una base a la otra.

\(A= \ frac{b_1 + b_2}{2}\: \ times\:h\)

Esta fórmula proporciona el área de un trapezoide con bases \(b_1\) y \(b_2\) y altura \(h\), definidas de la misma manera que para los paralelogramos.

Ángulos interiores de Polígonos regulares

\((n-2)\:\times\:180^{\circ}= S\)

En un polígono regular, donde todos los lados y ángulos son iguales, esta fórmula proporciona la suma \(S)\) de los ángulos interiores dados un polígono con \(n\) lados y ángulos. También podemos encontrar cada ángulo interior calculando \(\frac{S}{n}\).

Longitud del arco en un Círculo

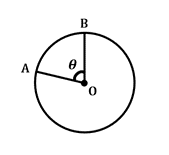
\(\frac {\theta} {360^{\circ}}\: \ times\:2\pi r=arco\:longitud\)

Esta fórmula define la longitud del arco, o sección de la circunferencia del círculo, entre dos radios dados que se cruzan en el centro del círculo con el ángulo central \(\theta\). Tenga en cuenta que \(2\pi r\) incorpora la circunferencia del círculo en esta fórmula.

Área del sector en un Círculo

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = sector\:área\)

Similar a la longitud del arco, esta fórmula proporciona el área del sector entre dos radios dados que se cruzan en el centro del círculo con ángulo central . El \(\pi r^2\) incorpora el área del círculo en esta fórmula.

Formas 3D

\(SA = 2 (lw + wh + lh)\)

\(V = lwh\)

Estas fórmulas proporcionan el área de superficie \((SA)\) y el volumen \(V)\) para un prisma rectangular con longitud \(l\), anchura \(w\) y altura \(h\).

\(V= \ pi r^2h\)

Esta es la fórmula de volumen para un cilindro derecho con radio de base \(r\) y altura \(h\).

Si necesita las fórmulas de área de superficie o volumen para cualquier otra forma 3D, el ACT proporcionará fórmulas relevantes en las propias preguntas.

Trigonometría

SOH-CAH-TOA

La mayoría de los problemas de trigonometría ACT implican manipular seno, coseno y tangente, que se calculan de la siguiente manera para un ángulo dado \(x\) en un triángulo rectángulo:

\(sin (x) = \frac{opuesto\: pierna}{hipotenusa}\)

\(cos (x)=\frac{adyacente\: pierna}{hipotenusa}\)

\(tan (x) = \frac{opuesto\: pierna}{adyacente\: pierna} = \frac {sin (x)} {cos (x)}\)

SOH-CAH-TOA es una mnemotécnica fácil para recordar qué función trigonométrica corresponde a qué longitudes de lado.

Identidades de Cofunción

\(sin (x) = cos (90^{\circ} – x)\)

\(cos ( x) = sin(90^{\circ}-x)\)

En palabras, estas identidades muestran que una función trigonométrica de ángulo \(x\) es igual al valor de la cofunción del complemento de \(x\). Generalmente se utilizan cuando se trata de trigonometría más avanzada, lo que permite conversiones fáciles entre seno y coseno.

Relación / Identidades Trigonométricas Recíprocas

Ocasionalmente puede ver las identidades recíprocas de \(sin (x)\), \(cos (x)\) y \(tan (x)\), que son:

\(csc(x) =\frac{1}{sin(x)}\)

\(sec(x) =\frac{1}{cos(x)}\)

\(cot(x) =\frac{1}{tan(x)}\)

Identidad Pitagórica

\(sen^2(x)+cos^2(x)=1\)

Basado en el Teorema de Pitágoras y el círculo unidad, esta identidad se utiliza generalmente junto con el cofunction identidades para resolver problemas de trigonometría (sin calculadora) donde el ángulo \(x\) o los valores de las funciones trigonométricas de \(x\) son desconocidos.

Estadística y probabilidad

Porcentajes

\(n\%\: de\: m = \ frac{n} {100}\: \ veces\:m\)

Los porcentajes se utilizan para expresar partes de un todo, y el símbolo \(\%\) generalmente significa “dividir por 100.”Como tal, la ecuación anterior responde a cualquier problema que pida \(n\%\) de cantidad \(m\).

Media, Mediana, Modo y Rango

El ACT prueba los conocimientos estadísticos básicos, generalmente con las siguientes medidas:

• La media es el promedio, o \(\frac{suma\: de\: todos\: términos}{total\: número\: de\:términos}\)
• Mediana es el término medio, o el promedio de los dos términos medios si hay un número par de términos
• Modo es el término(s) que ocurre con mayor frecuencia
• Rango es la diferencia entre los términos más grandes y más pequeños

Probabilidad

\(P(A) = \frac{número\:of\:deseado\:resultados}{total\:número\:de\:posibles\:resultados}\)

La probabilidad representa la probabilidad de que ocurra un evento \(A)\), calculado dividiendo el número de resultados deseados por el número de resultados posibles totales. Por ejemplo, la probabilidad de lanzar un 6 en un dado de lados pares es \(\frac{1}{6}\).

Eventos independientes

\(P(A\:and\:B) = P(A)\:\times\:P(B)\)

Los eventos \(A\) y \(B\) son independientes si la ocurrencia de \(A\) no afecta a la probabilidad de que ocurra \(B\). Para calcular la probabilidad de que ocurran ambos eventos independientes, multiplicamos sus probabilidades individuales juntas. Por ejemplo, la probabilidad de salir cara dos veces es \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

Terminando

Hemos cubierto muchas fórmulas en esta publicación, pero asegúrese de revisar también todos los conceptos matemáticos a través de Álgebra II y Geometría. Por ejemplo, puede esperar que números complejos, vectores, matrices, sistemas de ecuaciones y funciones gráficas de manipulación también estén en la prueba. Consulte esta descripción completa de la sección de matemáticas de ACT para obtener más información.

¡Recuerda que la práctica hace al maestro, especialmente para las matemáticas! Querrá probar muchos problemas diferentes antes del día del examen, con el objetivo de comprender realmente cómo aplicar e integrar estos conceptos y fórmulas de manera oportuna.

Como se le permite una calculadora para el ACTO, le recomendamos que traiga una, pero con una palabra de precaución. Recuerde que todos los problemas matemáticos de ACT se pueden resolver sin una calculadora, y es fácil perder un tiempo valioso usando su calculadora cuando en realidad no lo necesita. Como tal, haga secciones de práctica cronometradas con su calculadora si planea traer una, y recuerde que solo está allí como último recurso: para facilitar los cálculos y aumentar su velocidad. Tómelo con poca frecuencia y compruebe que su modelo específico está permitido según la política de calculadora de ACT.