31 zákon matematické vzorce, které potřebujete vědět

geometrie roviny

úhly a čáry

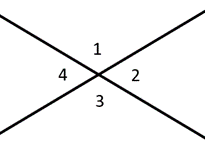
úhly podél čáry se nazývají doplňkové úhly, které se sčítají do \(180^{\circ}\). Komplementární úhly sčítají až \(90^{\circ}\), pravý úhel. Svislé úhly popisují úhly přímo naproti sobě, které jsou vždy shodné. Například v diagramu vlevo bychom řekli, že úhly 1 & 2 jsou doplňkové, zatímco úhly 1 & 3 jsou svislé úhly.

plocha trojúhelníku

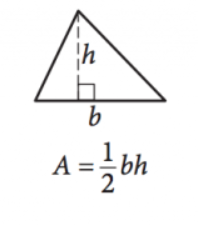
obrázek se svolením sat

\(\frac{1}{2}bh=a\)

tato rovnice poskytuje plochu \((a)\) libovolného trojúhelníku daných délek základny \((B)\) a výšky \((h)\). Všimněte si, že výška je délka čáry probíhající v komplementárním úhlu z kterékoli strany (základny) až k bodu/úhlu přímo naproti této straně.

pro rovnostranné trojúhelníky, kde všechny tři strany \((s)\) mají stejnou délku, rovnice plochy je:

\(\frac{s^2 \ sqrt{3}}{4}=a\)

Pythagorova věta

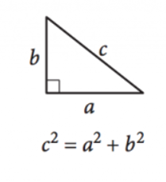
obrázek s laskavým svolením SAT

protože úhly v trojúhelníku vždy sčítají \(180^{\circ}\), pravoúhlý trojúhelník je definován jako libovolný trojúhelník s jedním pravým úhlem, což zajišťuje, že ostatní dva úhly se doplňují. Boční délky pravoúhlých trojúhelníků lze definovat Pythagorovou větou:

\(a^2+b^2=c^2\)

zde \(a\) A \(b\) jsou délky nohou nebo strany napříč od komplementárních úhlů a \(c\) je délka přepony, strana naproti pravému úhlu.

může být užitečné zapamatovat si také následující Pythagorovy trojnásobky nebo hodnoty pro délky stran \((a,b, c)\): 3-4-5, 5-12-13, 7-24-25, a 8-15-17. Všimněte si, že přepona je vždy nejdelší stranou.

speciální pravoúhlé trojúhelníky

existují dva typy speciálních pravoúhlých trojúhelníků, které mají úhly a délkové poměry takto:

obrázek se svolením sat

oblasti čtyřúhelníků

\(a = lw\)

tento vzorec poskytuje plochu obdélníku s délkou \(l\) a šířkou \(w\).

\(a = bh\)

tento vzorec poskytuje plochu rovnoběžníku dané základny \(b\), délku nejdelších stran a výšku \(h\), definovanou jako délka čáry probíhající v komplementárním úhlu nahoru od jedné základny k druhé.

\(A= \ frac{b_1+b_2}{2}\: \ krát\:h\)

tento vzorec poskytuje plochu lichoběžníku s bázemi \(b_1\) a \(b_2\) a výškou \(h\), definovanou stejným způsobem jako pro rovnoběžníky.

vnitřní úhly pravidelných mnohoúhelníků

\((n-2)\: \ krát\: 180^{\circ}= s\)

v pravidelném mnohoúhelníku, kde jsou všechny strany a úhly stejné, tento vzorec poskytuje součet \((s)\) vnitřních úhlů daného mnohoúhelníku s \(n\) stranami a úhly. Každý vnitřní úhel můžeme také najít výpočtem \(\frac{S}{n}\).

délka oblouku v kruhu

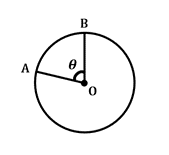
\(\frac {\theta}{360^{\circ}}\: \ krát\:2 \ pi r=oblouk\: délka\)

tento vzorec definuje délku oblouku nebo část obvodu kružnice mezi dvěma danými poloměry, které se protínají ve středu kružnice se středovým úhlem \(\theta\). Všimněte si, že \(2 \ pi r\) zahrnuje obvod kruhu do tohoto vzorce.

Plocha sektoru v kruhu

\(\frac {\theta}{360^{\circ}}\:\times\: \ pi r^2 = sektor\: Plocha\)

podobně jako délka oblouku tento vzorec poskytuje plochu sektoru mezi dvěma danými poloměry, které se protínají ve středu kruhu se středním úhlem . \(\Pi r^2\) zahrnuje kruhovou oblast do tohoto vzorce.

3D tvary

\(SA = 2 (lw + wh + lh)\)

\(V= lwh\)

tyto vzorce poskytují plochu \((SA)\) a objem \((V)\) pro obdélníkový hranol s délkou \(l\), šířkou \(w\) a výškou \(h\).

\(V= \ pi r^2h\)

Toto je objemový vzorec pro pravý válec s poloměrem základny \(r\) a výškou \(h\).

pokud potřebujete vzorce plochy nebo objemu pro jakékoli jiné 3D tvary, zákon poskytne příslušné vzorce v samotných otázkách.

trigonometrie

SOH-CAH-TOA

většina problémů act trig zahrnuje manipulaci s sinusem, kosinem a tečnou, které jsou vypočteny následovně pro daný úhel \(x\) v pravoúhlém trojúhelníku:

\(sin(x)= \ frac{naproti\: noha}{přepona}\)

\(cos (x)= \ frac{sousední\: noha}{přepona}\)

\(tan (x)=\frac{naproti\: noha}{sousední\: noha}=\frac{sin (x)}{cos (x)}\)

SOH-CAH-TOA je snadná mnemotechnická pomůcka pro zapamatování, která funkce trig odpovídá délkám stran!

Kofunkce

\(sin (x) = cos(90^{\circ} – x)\)

\(cos (x) = sin(90^{\circ}-x)\)

ve slovech tyto identity ukazují, že funkce trig úhlu \(x\) se rovná hodnotě kofunkce komplementu \(x\). Obvykle se používají při řešení pokročilejší trigonometrie, což umožňuje snadné převody mezi sinusem a kosinem.

Ratio / reciproční Trig identity

občas můžete vidět reciproční identity \(sin(x)\), \(cos (x)\) a \(tan (x)\), které jsou:

\(csc (x) =\frac{1}{sin (x)}\)

\(sek (x) =\frac{1}{cos (x)}\)

\(cot (x) =\frac{1}{tan (x)}\)

Pythagorova identita

\(sin^2(x)+cos^2 (x)=1\)

na základě Pythagorovy věty a jednotkové kružnice se tato identita obecně používá spolu s kofunkčními identitami k řešení problémů trig (sans calculator), kde úhel \(x\) nebo hodnoty těchto funkcí trig \(x\) nejsou známy.

Statistika a pravděpodobnost

procenta

\(n\%\: of\: m = \ frac{n}{100}\: \ times\:m\)

procenta se používají k vyjádření částí celku a symbol \ ( \ % \ ) obecně znamená ” dělit 100.”Jako taková výše uvedená rovnice odpovídá na jakýkoli problém, který žádá o \(n\%\) množství \(m\).

průměr, medián, režim a rozsah

Act testuje základní statistické znalosti, obvykle zahrnující níže uvedená opatření:

• průměr je průměr, nebo \(\frac{sum\: of\: all\: terms}{total\: number\: of\:podmínky}\)
• medián je střední termín, nebo průměr dvou středních termínů, pokud existuje sudý počet termínů
• režim je termín(Y), který se vyskytuje nejčastěji
• rozsah je rozdíl mezi největším a nejmenším termínem

Pravděpodobnost

\(P(a) = \frac{number\:of\:desired\:outcomes}{total\:number\:of\:possible\:výsledky}\)

pravděpodobnost představuje pravděpodobnost výskytu události \((a)\), vypočtená vydělením počtu požadovaných výsledků počtem celkových možných výsledků. Například pravděpodobnost válcování 6 na rovnoměrné kostky je \(\frac{1}{6}\).

nezávislé události

\(P (a\: A\: B) = P (a)\: \ times\: P (B)\)

události \(a\) A \(B\) jsou nezávislé, pokud \(a\) vyskytující se neovlivní pravděpodobnost výskytu \(B\). Abychom vypočítali pravděpodobnost, že dojde k oběma nezávislým událostem, vynásobíme jejich jednotlivé pravděpodobnosti dohromady. Například pravděpodobnost převrácení hlav dvakrát je \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

zabalení

v tomto příspěvku jsme pokryli spoustu vzorců, ale nezapomeňte také zkontrolovat všechny matematické koncepty prostřednictvím algebry II a geometrie! Můžete například očekávat, že komplexní čísla, vektory, matice, systémy rovnic a manipulace s grafickými funkcemi budou také v testu. Další informace naleznete v tomto úplném popisu části ACT math.

nezapomeňte, že praxe je perfektní, zejména pro matematiku! Budete chtít vyzkoušet spoustu různých problémů před testovací den, s cílem skutečně pochopit, jak aplikovat a integrovat tyto pojmy a vzorce včas.

vzhledem k tomu, že máte k dispozici kalkulačku, doporučujeme vám ji přinést, ale s opatrností. Nezapomeňte, že každý matematický problém ACT lze vyřešit bez kalkulačky a je snadné ztrácet drahocenný čas pomocí kalkulačky, když to skutečně nepotřebujete. Jako takový, proveďte časované tréninkové sekce s kalkulačkou, pokud ji chcete přinést, a pamatujte, že je to jen jako poslední možnost: pro usnadnění výpočtů a zvýšení rychlosti. Sáhněte po něm jen zřídka, a zkontrolujte, zda je váš konkrétní model povolen podle zásad kalkulačky act.