Isoquantova křivka: definice, vlastnosti, typy, předpoklady
co je isoquant Curve?
isoquant Curve: technická relace, která ukazuje, jak jsou vstupy převedeny na výstup, je znázorněna křivkou isoquant. Ukazuje optimální kombinace faktorových vstupů pomocí cen faktorových vstupů a jejich množství, která se používají k výrobě stejného výstupu.
termín ISO znamená rovnost a kvant znamená množství nebo výstup.
například pro výrobu 100 kalendářů se používá 90 jednotek kapitálu a 10 jednotek práce.
Isoquant křivky jsou také nazývány jako rovné křivky produktu nebo výrobní indiferenční křivky.
definice křivky Isoquant
předpoklady křivky Isoquant
předpoklady křivky isoquant jsou následující:
- k výrobě konkrétního produktu existují pouze dva faktorové vstupy, práce a kapitál.
- kapitál, práce a zboží jsou dělitelné povahy.
- kapitál a práce se mohou navzájem nahradit až do určité hranice.
- technologie výroby je dána po určitou dobu.
- výrobní faktory se používají s plnou účinností.
Naučme se isoquant pomocí následující tabulky.
Tabulka 1 ukazuje různé kombinace dvou faktorových vstupů, jmenovitě práce a kapitálu pro výrobu 150 tun produkce:
| práce | kapitál |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
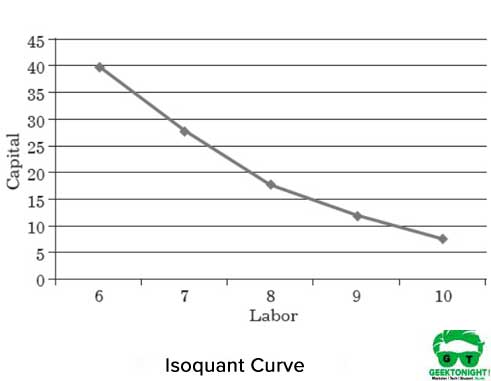
Obrázek 1 ukazuje izokvantovou křivku různých kombinací pracovního kapitálu, které pomáhají produkovat 150 tun produkce:
vlastnosti křivky Isoquant
některé z vlastností křivky isoquant jsou následující:
- Isoquant křivky sklon dolů
- Isoquant křivky jsou konvexní k původu
- isoquant křivky nemohou protínat navzájem
- vyšší isoquant čím vyšší je výstup

Isoquant křivky sklon dolů
to znamená, že sklon křivky isoquant je záporný. Je to proto, že když se zvýší kapitál (K), sníží se množství práce (L) nebo naopak, aby se zachovala stejná úroveň produkce.
Isoquant křivky jsou konvexní k původu
to znamená, že faktorové vstupy nejsou dokonalé náhražky. Tato vlastnost ukazuje substituci vstupů a klesající mezní rychlost technické substituce isoquantu. Mezní význam jednoho vstupu (kapitálu) z hlediska jiného vstupu (práce) se snižuje spolu s izokvantovou křivkou.
Obrázek 2 ukazuje konvexní izokvantovou křivku:
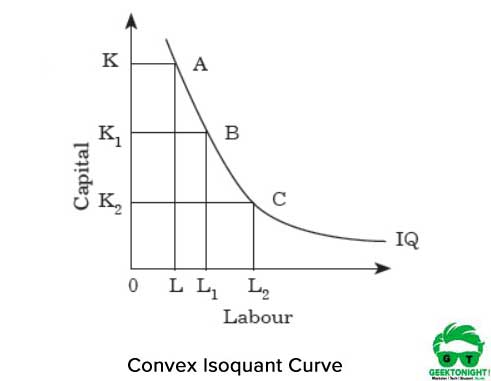
konvexita představuje, že MRT se zmenší, pokud se přesuneme z bodu A do B A Z B do C podél izokvantu. MRT se zmenšuje, protože dva vstupy práce a kapitál nejsou dokonalými náhradami.
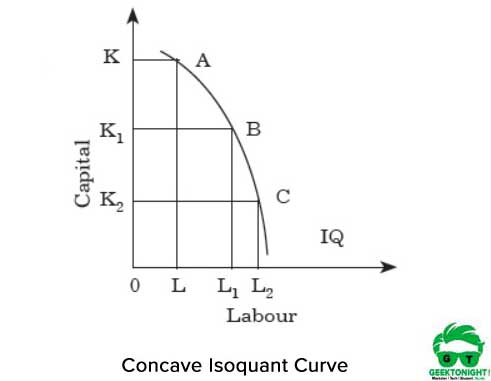
při každém zvýšení pracovní síly tedy dochází ke snížení kapitálu. Pokud je to konkávní, zvyšuje se MRT práce pro kapitál. Obrázek 3 ukazuje konkávní křivku isoquant:
jak je znázorněno na obrázku 3, pokud se pohybujeme z bodu A do B A Z B do C podél isoquantu, MRT se zvýší. Ukazuje se, že oba vstupy práce a kapitál jsou dokonalými náhradami. Při každém zvýšení pracovní síly tedy dochází ke zvýšení kapitálu.
isoquant křivky se nemohou vzájemně protínat
isoquant znamená různé úrovně kombinace produkující různé úrovně vstupů. Pokud se isoquanty protínají, znamenalo by to, že jedna vstupní kombinace může produkovat dvě úrovně výstupu, což není možné. Výrobní právo by nebylo použitelné.
vyšší isoquant čím vyšší je výstup
znamená to, že vyšší isoquant představuje vyšší výstup. Horní křivka izokvantu produkuje více výkonu než křivka pod ní. Je to proto, že větší kombinace vstupů má za následek větší výstup ve srovnání s křivkou, která je pod ní.
mezní rychlost technické substituce
sklon křivky isoquant je rychlost substituce, která ukazuje, jak může být jeden vstup nahrazen jiným, zatímco drží výstupní konstantu. Tomu se říká mezní míra technické substituce (MRT).
podle Lipsey, ” mezní rychlost technické substituce může být definována jako rychlost, při které je jeden faktor nahrazen jiným s výstupem udržovaným konstantní.”
vzorec pro výpočet MRT je následující:
MRTS = – ∆K / L L
kde, ∆k = Změna kapitálu
∆L= změna práce
vzorec ukazuje, že na dané úrovni produkce by MRTS kapitálu pro práci znamenaly množství práce, které by byla firma ochotna vzdát za další jednotku kapitálu. Podobně MRT práce pro kapitál by znamenalo množství kapitálu, které by firma byla ochotna vzdát za další jednotku práce.
MRT se také rovná poměru mezního součinu jednoho vstupu k meznímu součinu jiného vstupu. Výstup podél isoquantu je konstantní. Je-li změna pracovní síly nahrazena změnou kapitálu, pak by zvýšení produkce v důsledku zvýšení pracovní síly mělo odpovídat poklesu produkce v důsledku snížení kapitálu. Matematicky
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Protože výstup zůstává beze změny na daném isoquant,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
můžeme Tedy říci, že MRTS mezi vstupy se rovnají mezní produkty na vstupy.
MRTS se vypočítá podle tabulky 2
| práce | kapitál | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
typy křivky Isoquant
dochází ke kontinuálnímu nahrazování jedné vstupní proměnné druhou vstupní proměnnou s klesající rychlostí. Dokonalé doplňky a dokonalé náhražky dávají různé formy izokvantů.
různé typy křivky isoquant jsou následující:
- Lineární isoquant
- isoquant ve tvaru písmene L

Lineární isoquant
jedná se o přímku isoquant a představuje dokonalou nahraditelnost mezi vstupy, kapitálem a prací výrobní funkce. MRT mezi vstupy zůstává konstantní. Obrázek 4 ukazuje lineární izokvant:
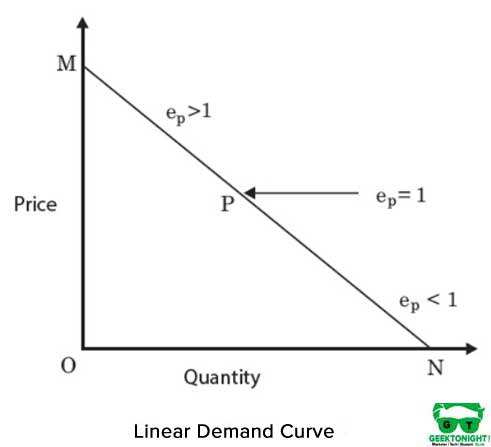
algebraická forma výrobní funkce v případě lineárního izokvantu je následující:
Q = ak + BL
zde Q je vážený součet K A L. sklon křivky lze vypočítat pomocí následujícího vzorce:
MPK = Q Q/∆K = a
MPL = Q Q / L L = B
MRTS = MPL / MPK
MRTS = – b / a (b/a je konstantní)
lineární isoquant však v reálném světě neexistuje.
isoquant ve tvaru písmene L
to je případ dokonalých doplňků. V rámci toho je kombinace kapitálu a práce v pevném poměru. Pouze jedna kombinace práce a kapitálu je možné vyrobit produkt s připojeným podílem vstupů.
pro zvýšení produkce musí organizace přiměřeně zvýšit oba vstupy. Grafické znázornění poměru fixního faktoru isoquant je ve tvaru L, znázorněno na obrázku 5:
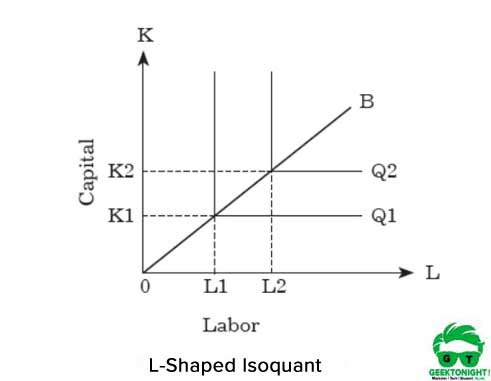
jak je znázorněno na obrázku 5, izokvant ve tvaru písmene L představuje, že neexistuje náhrada mezi prací a kapitálem a předpokládá se, že se jedná o doplňkové zboží. Je vidět, že pro výrobu Q1 jsou vyžadovány jednotky kapitálu OK1 a jednotky práce OL1.
na druhé straně, aby se zvýšila produkce z Q1 na Q2, musí organizace zvýšit vstupy z K1 na K2 a L1 na L2. Tento vztah mezi kapitálem a prací lze vyjádřit následovně:
Q = f (K, L) = min (aK, bL)
kde min znamená Q rovná se nižší ze dvou výrazů, aK a bL
například v případě ak > bL, pak Q = bL a v případě ak < bL pak Q = aK.
tento isoquant je stejný jako funkce výroby leontif.
Elasticita substituce mezi faktory
víme, že MRT je sklon izokvantu. Neodhaluje však stupeň nahraditelnosti jednoho faktoru do druhého. Je důležité měřit stupeň nahraditelnosti mezi dvěma vstupy.
proto ekonomové vyvinuli vzorec pro odhad rozsahu nahraditelnosti mezi dvěma vstupy, kapitálem a prací, který je známý jako elasticita substituce faktorů.
Elasticita substituce faktoru (σ) označuje poměr procentuální změny poměru kapitál-práce k procentuální změně MRT.
je matematicky reprezentován takto:
σ = procentní změna poměru kapitálové práce / procentní změna MRT
nebo,
σ = *
If ∆K / L L = Mr MRTS ; σ = 1
Pokud ∆K/∆L > ∆MRTS ; σ > 1
Pokud ∆K/∆L < ∆MRTS ; σ < 1
Vysoká elasticita substituce mezi faktory, znamená to, že faktory mohou být snadno nahradit navzájem, zatímco nízká pružnost představuje, že substituce faktorů je možné do určité míry.
v případě lineárního izokvantu by substituční Elasticita byla nekonečná a v případě izokvantů ve tvaru L by byla nulová.
ISO nákladové křivky
Iso-nákladová křivka je lokus bodů všech různých kombinací práce a kapitálu, které může organizace zaměstnat, vzhledem k ceně těchto vstupů. Iso-cost line představuje cenu faktorů spolu s množstvím peněz, které je organizace ochotna utratit za faktory.
jinými slovy, ukazuje různé kombinace faktorů, které lze zakoupit za určitou částku peněz. Sklon iso-nákladové linie závisí na poměru ceny práce k ceně kapitálu.
například výrobce má celkový rozpočet 120 120 ,který chce utratit za výrobní faktory, jmenovitě X a Y. Cena X na trhu je ₹15 za jednotku a cena Y je ₹10 za jednotku. Tabulka 7.5 zobrazuje kombinace:
| kombinace | jednotky x | jednotky Y | celkové výdaje |
|---|---|---|---|
| v | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
řádek iso-cost je znázorněn na obrázku 7.8:
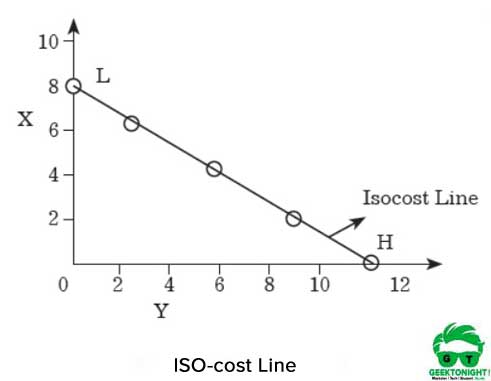
jak je znázorněno na obrázku 6, pokud výrobce utratí celou částku peněz na nákup X, pak může koupit 8 jednotek X. na druhou stranu, pokud výrobce zakoupí Y s celou částkou, pak by mohl získat 12 jednotek.
pokud jsou body H a L spojeny na osách X a Y, získá se přímka, která se nazývá ISO-nákladová čára. Všechny kombinace X a Y, které leží na tomto řádku, by měly stejnou cenu, která je ₹120.
podobně mohou být vykresleny i jiné ISO-cost linky tím, že náklady převyšují 120, V případě, že je výrobce ochoten vynaložit více peněz na výrobní faktory.
s pomocí linek isoquant a iso-cost může výrobce určit bod, ve kterém vstupy přinášejí maximální zisk vynaložením minimálních nákladů. Takový bod se nazývá rovnováha producenta.
Přečtěte Si Také: Cardinal a Ordinal Utility
Business Economics Tutorial
(klikněte na téma ke čtení)
pokračujte, sdílejte článek s přáteli
Leave a Reply