jaké jsou různé typy proudění tekutin-úplné vysvětlení

Úvod do tekutiny

tekutina je látka, která má tendenci se deformovat nepřetržitě pod smykovým napětím. Skládá se z kapaliny i plynů. Všechny záležitosti na zemi lze rozdělit na základě jejich chování do dvou kategorií, tj. Látka, která má tendenci proudit za určitých daných podmínek, se nazývá tekutina. Pro lepší pochopení a vizualizaci typů proudění tekutin je nezbytné porozumět různým typům tekutin a rozdílu mezi tekutinou a pevnou látkou. V tomto článku budeme stručně diskutovat o typech tekutin a rozdílu mezi pevnou látkou a tekutinou a poté přejdeme na typy proudění tekutin.

typy tekutin

kapaliny jsou klasifikovány na základě jejich chování při Smykovém napětí. Chování je analyzováno pomocí veličiny zvané viskozita a hustota tekutiny. Viskozita je jako třecí síla přítomná v pevných částicích, které odolávají pohybu pevné látky. Odolává toku tekutiny a indukuje relativní pohyb mezi následnými vrstvami tekutiny.

Chcete-li klasifikovat a lépe porozumět klasifikaci, zvažte následující rovnici:

Poznámka: Výše uvedená rovnice představuje tekutinu proudící v jednom směru (směr X) a tok ve všech ostatních směrech je nulový.

tekutinu můžeme klasifikovat do 6 různých typů, které jsou diskutovány následovně:

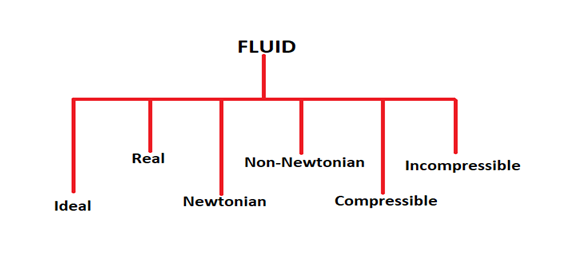
1. Ideální tekutina:

v tomto typu tekutiny je viskozita považována za nulovou a hustota je všude konstantní. To znamená, že mezi vrstvami tekutiny v toku tekutiny nedochází k relativnímu pohybu a všechny vrstvy se pohybují stejnou rychlostí. Ideální tekutina je předpoklad a ve skutečnosti nejsou přítomny. Tyto předpoklady jsou vytvořeny pro analýzu chování nějaké tekutiny za daných podmínek.

Stručně řečeno, můžeme říci, že,

2. Skutečná tekutina:

v tomto typu tekutiny není viskozita nulová a hustota se mění všude v tekutině. To znamená, že existuje relativní pohyb mezi vrstvami tekutiny v toku tekutiny. Skutečná tekutina je chování, které má tekutina ve skutečnosti, ale je často ignorováno, aby byla analýza jednodušší. V reálné tekutině nemáme žádný pevný vzorec pro změnu hustoty a pevnou hodnotu viskozity tekutiny. Všechny tekutiny jsou skutečné tekutiny v přírodě.

Stručně řečeno, můžeme říci, že,

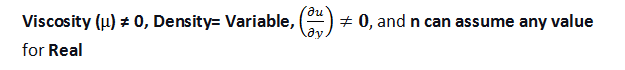
3. Newtonovská tekutina:

v reálné tekutině nemáme přesný vzorec pro výpočet hustoty a neznáme viskozitu tekutiny. Newtonovská tekutina je tekutina s definovanou hodnotou viskozity a hodnota exponentu (n) je 1. Rovnici pro všechny newtonovské tekutiny lze zapsat následovně:

newtonovská tekutina může mít konstantní a proměnnou hustotu, ale změna hustoty

s ohledem na čas a prostor nám bude známa.

Stručně řečeno, můžeme říci, že,

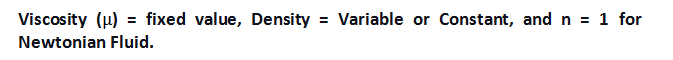
4. Nenewtonská tekutina:

u tohoto typu tekutiny není viskozita nulová a je přesně definována. Hustota se může měnit nebo zůstat konstantní s ohledem na čas a prostor. Hlavní rozdíl vzniká s hodnotou exponentu ‘n’, která není rovna 1 a závisí na typu nenewtonovské tekutiny. Rovnici pro všechny nenewtonovské tekutiny lze zapsat následovně:

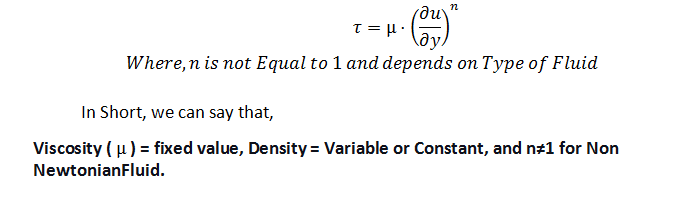
5. Stlačitelná Tekutina:

o tekutině se říká, že je stlačitelná tekutina, pokud se hustota mění s časem a prostorem. V tomto případě nemůžeme říci o viskozitě, protože může být nulová nebo nenulová.

Stručně řečeno, můžeme říci, že,

6. Nestlačitelná tekutina:

o tekutině se říká, že je nestlačitelná, pokud se hustota tekutiny nemění s časem a prostorem. V tomto případě nemůžeme říci o viskozitě, protože může být nulová nebo nenulová.

Stručně řečeno, můžeme říci, že,

níže uvedená klasifikace uvádí vlastnost různých tekutin na základě jejich viskozity a hustoty:

S.no.	typ kapaliny	viskozita	hustota
1	ideální tekutina	nula	konstanta
2	reálná tekutina	nenulová	proměnná
3	newtonovská tekutina	nenulová a má určitý vzorec	může být buď konstantní nebo proměnná
4	Nenewtonská tekutina	nenulová a vzorec závisí na typu nenewtonské tekutiny	může být buď konstantní nebo proměnná
5	stlačitelná tekutina	nula / nenulová	proměnná
6	nestlačitelná tekutina	nula / nenulová	konstanta

pevná látka vs tekutina: rozdíly mezi nimi

pevná látka a tekutina se liší svým chováním a nedodržují pravidla fyziky stejným způsobem. Vzhledem k jejich rozdílným vlastnostem máme pevnou mechaniku pro pevnou a tekutou mechaniku pro tekutinu. Můžeme si všimnout mnoha rozdílů mezi nimi, protože pečlivě sledujeme jejich chování za různých podmínek. Pro seskupení jejich chování do jednoduššího způsobu používáme vlastnost zvanou smykové napětí. Definuje tokovou vlastnost tekutiny a to, jak se její chování liší od pevných látek. Pevné látky mají tendenci se ohýbat a deformovat působením smykového napětí. Proto se jejich smykové napětí mění lineárně s ohybem nebo deformací. Tekutina má tendenci se deformovat nepřetržitě působením smykového napětí a variace smykového napětí není lineární s deformací. To je hlavní rozdíl mezi pevnou a tekutinou.

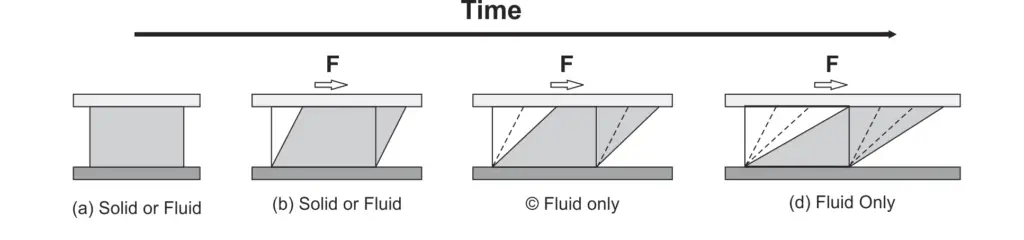
Obr: smykové napětí chování

hnací síla pro proudění kapaliny

průtokové charakteristiky kapaliny vedou k různým jevům, jako je cyklon, změna počasí, chlazení spalovacího motoru a mnoho dalších věcí. Vyvstává otázka, Jaký je důvod pro tok tekutiny? A můžeme předpovědět chování proudění tekutin za všech podmínek? Tekutina proudí z jednoho bodu do druhého kvůli tlakovému rozdílu mezi těmito dvěma body. Přirozený tok tekutiny nastává z vysokotlakého na nízkotlaký, aby se vyrovnal tlakový rozdíl v těchto dvou bodech. Průtok z nízkotlaké do vysokotlaké oblasti lze dosáhnout vnější hnací silou, jako je čerpadlo atd. Vzory proudění tekutin lze klasifikovat, ale nelze je přesně předpovědět v okamžiku. Veškerá predikce chování toku tekutin se provádí pomocí softwarů, které používají numerické techniky k přiblížení chování toku v daném okamžiku.

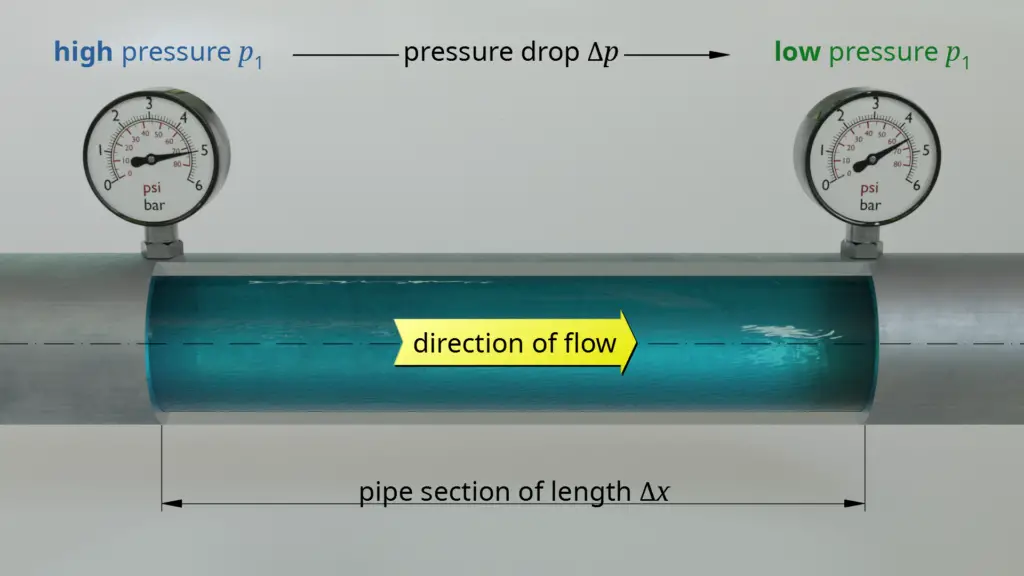
Zdroj obrázku

Chcete-li zahájit naši studii o toku tekutin, nejprve se dozvíme o různých parametrech v toku tekutin. Tyto parametry jsou časové osy, Pathlines, Streaklines a Streamlines.

Časová osa:

označíme-li sousední částice tekutiny proudící v daném okamžiku, vytvoří časovou osu. Například pro demonstraci chování tekutých částic za působení konstantního smykového napětí byla zavedena časová osa, která poskytla deformaci tekutiny v každém okamžiku. Proto, v časové ose, každá částice tekutiny je sledována v daném okamžiku.

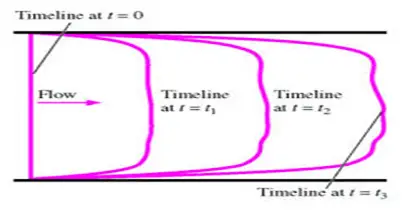
obr.4: Časová osa

Pathline:

pokud sledujeme cestu částice tekutiny po určitou dobu, vytvoří Pathline. Vezměte například barvivo a kouř a pořiďte dlouhou expoziční fotografii jeho následného pohybu. Cesta sledovaná částicí je Pathline. Zde považujeme zdrojovou částici tekutiny a pozorujeme její cestu po určitou dobu. Cesta sledovaná částicemi během této doby je dráha částice.

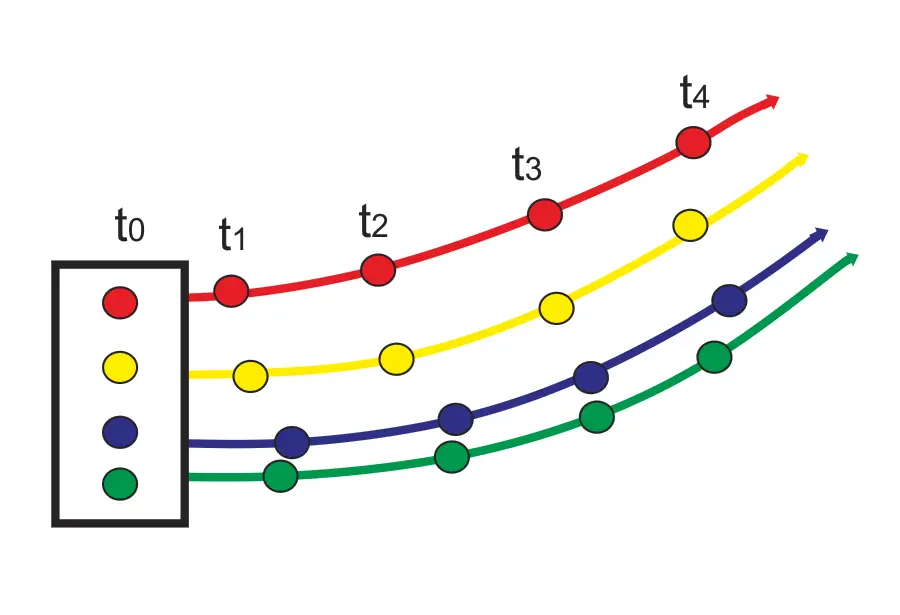
obr.: Pathline

Streakline:

pokud označíme dráhu částic tekutiny v daném místě po určitou dobu, vytvoří Streakline. Při aerodynamickém testování aerodynamického tunelu automobilu se směrem k vozu uvolňuje kouř pro vyhodnocení aerodynamické síly a odporu. Cesta sledovaná kouřem nad autem je pruhovaná. Zde zvažujeme tok následujících vrstev, pozorujeme jejich polohu v daném okamžiku a sledujeme polohu, aby se vytvořila Pruhová linie.

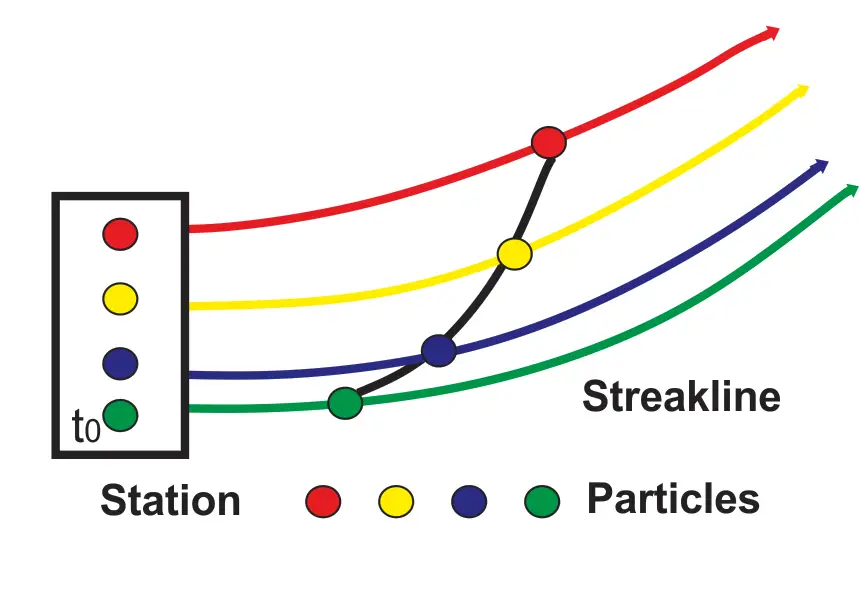
Obr: Streakline

Streamline:

je to dráha nakreslená pro tekutou částici tak, že tečna k ní udává směr rychlosti tekutých částic v bodě. Vzhledem k tomu, že jsou tečnou k toku, nemůže dojít k toku podél proudu. Používají se v počítačové simulaci pro vizualizaci toku, kde jsou nakresleny proudnice, které představují rychlostní pole sledované částicemi tekutiny.

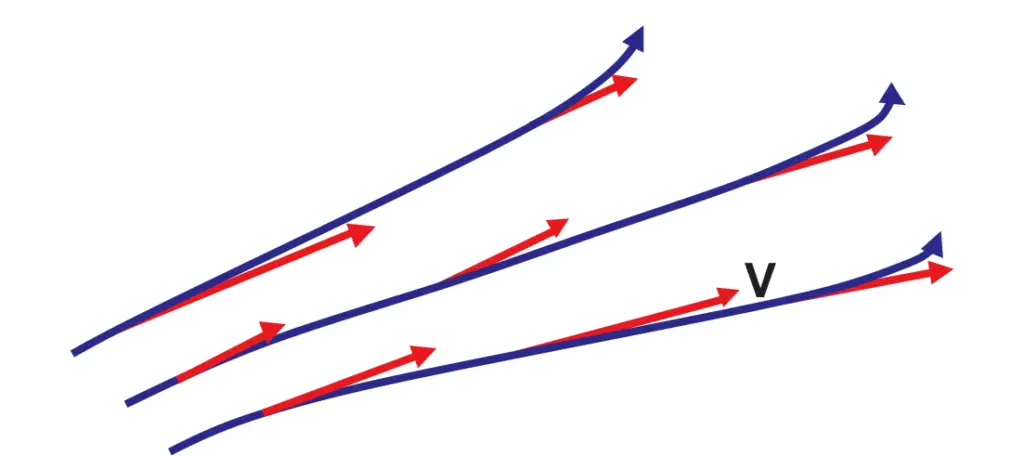
obr.: Streamline

typy proudění tekutin

tok tekutin lze rozdělit do následujících typů:

1. rovnoměrný a nejednotný tok
2. stálý a nestálý Tok
3. rotační a Irrotační Tok
4. stlačitelný a nestlačitelný Tok
5. viskózní a Neviskózní Tok
6. vnější a vnitřní tok
7. laminární a turbulentní tok
8. 1D, 2D a 3D Tok

studujme o nich jeden po druhém:

1. Rovnoměrný a nejednotný Tok

proudění tekutiny je prý rovnoměrné, pokud se rychlost tekutiny nemění s prostorem. Proto, v tomto typu proudění tekutiny, rychlost je závislá pouze na čase a ne na X, Y, Z souřadnic kapalné částice.

tok tekutiny se říká, že je nerovnoměrný, pokud se rychlost tekutiny mění s prostorem. Proto v tomto typu toku je rychlost funkcí času a X, Y, Z souřadnic tekutých částic. Například, jak je znázorněno na obrázku, rychlost proudění je konstantní, když se plocha průřezu nemění, ale jak se plocha průřezu mění, rychlost se mění, jak se tekutina pohybuje do řezu. Tok se stává non-Unifrom v přírodě.

tok tekutiny potrubím s rovnoměrným průřezem se nazývá rovnoměrný tok a pokud je tok tekutiny potrubím bez rovnoměrného (nebo zúženého ) průřezu, nazývá se nerovnoměrný tok

2. Stálý a nestálý tok

průtok tekutiny se říká, že je stabilní, pokud se vlastnosti tekutin, jako je rychlost a tlak, nemění s časem. Proto v tomto toku jsou vlastnosti tekutiny závislé pouze na souřadnicích X, Y, Z částice tekutiny. Pro tento typ toku jsou pruhy, proudy a cesty identické.

tok tekutiny je nestabilní, pokud se vlastnosti tekutiny, jako je rychlost a tlak, mění s časem. Proto v tomto toku jsou vlastnosti tekutiny závislé na čase a souřadnicích X, Y, Z částice tekutiny. Pro tento typ toku nejsou pruhy, proudy a cesty identické.

na daném obrázku první výraz představuje stálý tok, zatímco druhý výraz je pro nestabilní tok. Konstantní vypouštění potrubím bude stálý tok, zatímco variabilní vypouštění potrubím bude nestabilní tok.

3. Rotační a Irrotační Tok

pokud se částice tekutiny otáčejí kolem své osy při pohybu v proudu, nazývá se to Rotační tok.
pokud se částice tekutiny pohybují v proudu a neotáčejí se kolem své osy, nazývá se to Irrotační tok.
tento typ toku můžeme identifikovat výpočtem vířivosti toku, která závisí na rychlosti proudění. Pokud je Vorticita nulová, tok tekutiny je Irrotační; jinak je to rotační tok.

4. Stlačitelný a nestlačitelný Tok

v Stlačitelném toku se hustota tekutiny mění s časem a prostorem. Zatímco v Nestlačitelném toku zůstává hustota tekutiny konstantní. Tento tok nachází uplatnění v brzdové kapalině. V brzdovém systému brzdová kapalina přenáší tlak vytvořený nohou na kola pro rozbití. Pokud je kapalina nestlačitelná, přenese přesný tlak vyvíjený nohou na kola pro účinné brzdění. Pokud je kapalina stlačitelná, Tlak přenesený na kolo bude menší než aplikovaný. Může to být dokonce nula. Proto by brzdová kapalina měla být nestlačitelná.

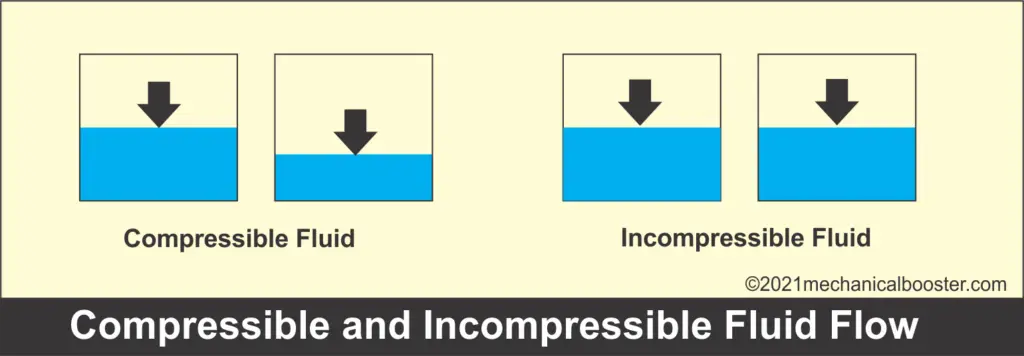
tyto typy proudění tekutin můžeme rychle identifikovat pomocí Machova čísla. Je definován jako:

Ma = V / Vs

• Vs= rychlost zvuku v tekutině
• V= rychlost tekutiny

0<=Ma<0.33	nestlačitelný tok
Ma>0.33	stlačitelný tok

5. Viskózní a Neviskózní Tok:

ve viskózním toku dochází k viskozitě tekutých částic mezi následujícími vrstvami, a proto dochází k relativnímu pohybu mezi vrstvou tekutých částic. V Neviskózním toku částice tekutin mezi následujícími vrstvami nezaznamenávají žádnou viskozitu, a proto mezi částicemi tekutiny nedochází k relativnímu pohybu.

6. Vnější a vnitřní tok:

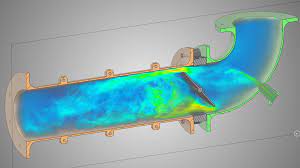
vnitřní tok tekutiny

přítomnost stěny určuje tento typ toku. Tok zcela ohraničený pevným tělesem se nazývá vnitřní tok nebo průtok potrubí.

pokud žádné pevné tělo neváže Tok, nazývá se to vnější Tok. Například tok přes automobil se nazývá externí tok, který je vizualizován pomocí softwaru a testu aerodynamického tunelu. Průtok uvnitř kruhové trubky je vnitřní tok a lze jej snadno vizualizovat pomocí softwarů a jednoduchých laboratorních experimentů.

7. Laminární a turbulentní proudění

při laminárním proudění se částice tekutiny pohybují v různých vrstvách a makroskopicky se nemíchají. V tomto typu toku tekutiny můžeme předpovědět vzorec toku v daném okamžiku. Všechny následující vrstvy jsou v toku vzájemně rovnoběžné.

v turbulentním proudění se částice tekutiny prolínají a tok se stává náhodným. Vzorec toku nelze přesně předpovědět v daném okamžiku v tomto typu toku. Dochází k tvorbě vírů, což vede k velkému množství energetických ztrát.

Reynoldsovo číslo se používá k predikci proudění, tj., zda je turbulentní a laminární. Vzorec je dán:

Re = v * L / µ

kde,

• Re = Reynoldsovo číslo
• V = rychlost tekutiny
• L = charakteristika délka objektu, kde probíhá proudění
• µ= koeficient viskozity

pro vnitřní proudění,

0<=Re<=2000	laminární proudění
2000<Re<=4000	přechod z laminárního na turbulentní
4000<Re	turbulentní proudění

pro vnější Tok,

0< =Re<=100000	laminární proudění
100000<Re<=500000	přechod z laminárního na turbulentní
500000<Re	turbulentní proudění

8. 1-D, 2-D a 3-D tok tekutiny:

v 1-D typu toku tekutiny jsou parametry tekutiny, jako je rychlost, funkcí času a pouze jedné prostorové souřadnice.

u 2-D typů proudění tekutin jsou parametry tekutiny, jako je rychlost, funkcí času a dvou prostorových souřadnic.

v 3 – D toku tekutiny jsou parametry tekutiny, jako je rychlost, funkcí času a všech tří prostorových souřadnic.

1-D průtok tekutiny	u= f (x, t), v=0 a w=0
2-D průtok tekutiny	u= f(x,y,t), v=g(x,y, t), w=0
3-D tok tekutiny	u= f(x,y,z,t), v=g(x,y,Z,t), w=h(x,y,z, t)

Časté dotazy

Q.1. Jaký je rozdíl mezi stlačitelnou tekutinou a stlačitelným tokem?

odpověď-stlačitelná tekutina hovoří o tekutině a její změně hustoty, zatímco stlačitelný tok hovoří pouze o tekutině v pohybu a o změně hustoty tekutiny v pohybu. Tekutina může mít konstantní hustotu během statických podmínek a proměnnou hustotu během dynamického stavu. Machovo číslo určuje, zda je tok stlačitelný nebo ne. Nerozhoduje o vlastnostech kapaliny.

Q. 2. Jaký typ toku tekutiny je zvažován v přechodovém režimu?

odpověď – záleží na situaci a stavu vašeho počítače. Pokud máte hodnotu blízkou turbulentnímu v přechodovém režimu a máte vynikající počítač pro simulaci, jděte na turbulentní. Pokud ne, pak jděte na Laminar.

Q. 3. Je proud vzduchu procházející autem je vnější a vnitřní tok

Odpověď – Pokud analyzujeme aerodynamický odpor automobilu, jedná se o vnější Tok. Uvnitř auta je určité množství vzduchu. Vzhledem k tomu, že je ohraničen pevnou látkou, lze jej tedy považovat za vnitřní tok.

Q.4. Jaký je název zákona, který se používá při aplikaci brzdové kapaliny?

odpověď-název zákona je Pascalsův zákon. Uvádí, že u nestlačitelné kapaliny je tlak přenášen rovnoměrně ve všech směrech.

Q. 5. Proč není časová osa zmíněna v ustáleném a nestabilním toku?

odpověď-neexistuje žádný koncept časové osy pro stálý průtok, protože parametry tekutiny nezávisí na čase.

Q. 6. Co je čerpadlo?

odpověď-čerpadlo je vnější činidlo, které se používá při pohybu tekutiny proti jejich přirozenému směru proudění. Například čerpadlo se používá v parní elektrárně pro odběr vody z kondenzátoru do kotle ve výšce.

Q. 7. Co je smykové napětí?

odpověď-smykové napětí je napětí vyvinuté silou působící tangenciálně na objekt, na který je síla aplikována.