Curva Isocuanta: Definición, Propiedades, Tipos, Supuestos
¿Qué es la Curva Isocuántica?
Curva isocuanta: Una relación técnica que muestra cómo se convierten las entradas en salida se representa mediante una curva isocuanta. Muestra las combinaciones óptimas de insumos de factores con la ayuda de los precios de los insumos de factores y sus cantidades que se utilizan para producir la misma producción.
El término ISO implica igual y quant significa cantidad o salida.
Por ejemplo, para producir 100 calendarios se utilizan 90 unidades de capital y 10 unidades de trabajo.
Las curvas isocuantas también se denominan curvas de producto iguales o curvas de indiferencia de producción.
Definición de curva Isocuanta
Supuestos de la Curva isocuanta
Los supuestos de una curva isocuanta son los siguientes:
- Solo hay dos factores, el trabajo y el capital, para producir un producto en particular.
- El capital, el trabajo y los bienes son de naturaleza divisible.
- El capital y el trabajo pueden sustituirse hasta cierto límite.
- La tecnología de producción se administra durante un período de tiempo.
- Los factores de producción se utilizan con plena eficiencia.
Aprendamos isoquant con la ayuda de la siguiente tabla.
la Tabla 1 muestra las diferentes combinaciones de dos factores de producción, a saber, el trabajo y el capital para producir 150 toneladas de producto:
| de Trabajo | Capital |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
La figura 1 muestra la curva isocuanta de diferentes combinaciones de capital laboral que ayudan a producir 150 toneladas de producción:
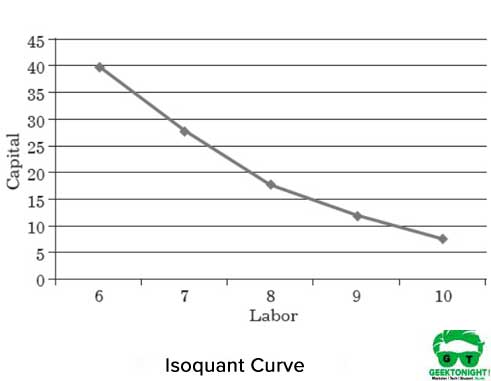
Propiedades de la curva Isocuanta
Algunas de las propiedades de la curva isocuanta son las siguientes:
- Las curvas Isocuant se inclinan hacia abajo
- Las curvas Isocuant son convexas al origen
- Las curvas Isocuant no pueden intersectarse entre sí
- Más alto el isocuant cuanto mayor sea la salida

Las curvas isocuantas se inclinan hacia abajo
Implica que la pendiente de la curva isocuanta es negativa. Esto se debe a que cuando se aumenta el capital (K), la cantidad de trabajo (L) se reduce o viceversa, para mantener el mismo nivel de producción.
Las curvas isocuantes son convexas al origen
Implica que las entradas de factores no son sustitutos perfectos. Esta propiedad muestra la sustitución de insumos y la tasa marginal decreciente de sustitución técnica de isocuant. La importancia marginal de un insumo (capital) en términos de otro insumo (trabajo) disminuye junto con la curva isocuanta.
La Figura 2 muestra la curva isocuanta convexa:
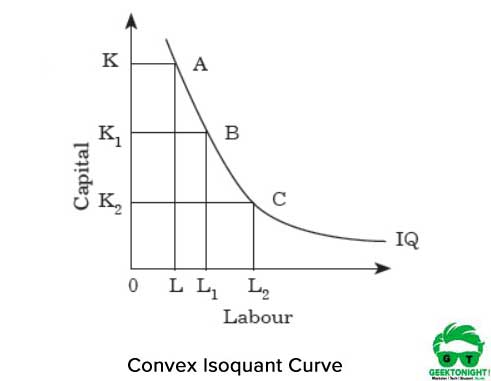
La convexidad representa que el MRTS disminuye si nos movemos del punto A al B y de B al C a lo largo de la isocuanta. El MRT disminuye porque los dos insumos, el trabajo y el capital, no son sustitutos perfectos.
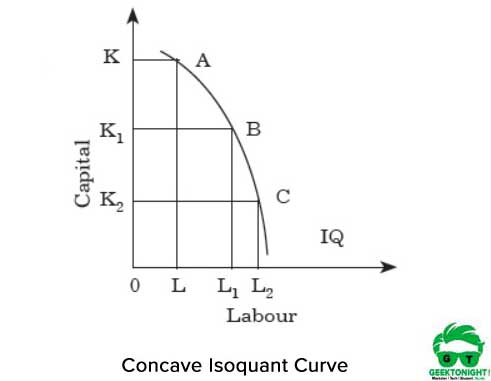
Por lo tanto, por cada aumento de la mano de obra, hay una disminución del capital. Si isocuant es cóncava, los MRT de mano de obra para aumentos de capital. La Figura 3 muestra la curva de isocuanta cóncava:
Como se muestra en la Figura 3, si nos movemos del punto A al B y de B al C a lo largo de la isocuanta, el MRTS aumenta. Muestra que los dos insumos, el trabajo y el capital, son sustitutos perfectos. Por lo tanto, por cada aumento en el trabajo, hay un aumento en el capital.
Las curvas isocuantas no pueden cruzarse entre sí
Una isocuanta implica los diferentes niveles de combinación que producen diferentes niveles de entradas. Si los isocuantes se cruzan entre sí, implicaría que una sola combinación de entrada puede producir dos niveles de salida, lo que no es posible. La ley de producción no sería aplicable.
Mayor es la isocuanta mayor es la salida
Implica que la isocuanta más alta representa una salida más alta. La curva superior de la isocuanta produce más salida que la curva inferior. Esto se debe a que la combinación más grande de entrada da como resultado una salida más grande en comparación con la curva que está debajo de ella.
Tasa marginal de Sustitución Técnica
La pendiente de la curva isocuanta es la tasa de sustitución que muestra cómo una entrada puede sustituirse por otra mientras mantiene la constante de salida. Esto se denomina tasa marginal de sustitución técnica (MRT).
Según Lipsey, “la tasa marginal de sustitución técnica puede definirse como la tasa a la que un factor se sustituye por otro con una salida constante.”
La fórmula para calcular los MRT es la siguiente:
MRTS = – K K / L L
donde, ∆K = Cambio en el capital
L L = Cambio en el trabajo
La fórmula muestra que, a un nivel dado de producción, los MRTS de capital para el trabajo implicarían la cantidad de trabajo que la empresa estaría dispuesta a renunciar por una unidad de capital adicional. Del mismo modo, los MRT de trabajo por capital implicarían la cantidad de capital que la empresa estaría dispuesta a renunciar por una unidad adicional de trabajo.
MRTS es también igual a la relación entre el producto marginal de un insumo y el producto marginal de otro insumo. La salida a lo largo de la isocuanta es constante. Si el cambio en el trabajo es sustituido por el cambio en el capital, entonces el aumento en la producción debido al aumento en el trabajo debe coincidir con la disminución en la producción debido a la disminución en el capital. Matemáticamente
∆L x PML= ∆K x Pmk
∆Q= ∆L x MPL + ∆K x Pmk
a partir de la salida permanece sin cambios en un determinado isoquant,
∆L x MPL + ∆K x Pmk = 0
(MPL / PMK)= (- ∆K / ∆L)
MRTSKL = (MPL / PMK)
por Lo tanto, podemos decir que MRTS entre las variables de entrada es igual a la marginal de los productos de las entradas.
El MRT se calcula como se muestra en la Tabla 2
| de Trabajo | Capital | MRT |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
Tipos de curva Isocuanta
Hay una sustitución continua de una variable de entrada por la otra variable de entrada a una velocidad decreciente. Complementos perfectos y sustitutos perfectos dan diferentes formas de isoquants.
Los diferentes tipos de curva isocuanta son los siguientes:
- Isoquante lineal
- Isoquante en forma de L

Isocuanta lineal
Es una isocuanta lineal y representa una sustituibilidad perfecta entre los insumos, el capital y el trabajo de la función de producción. Los MRT entre entradas permanecen constantes. La Figura 4 muestra una isocuanta lineal:
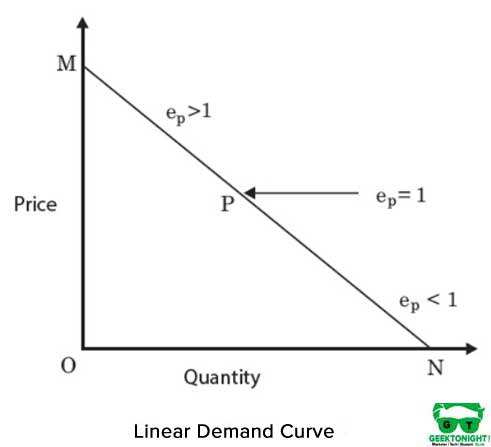
La forma algebraica de la función de producción en caso de isocuanta lineal es la siguiente:
Q = aK + BL
Aquí, Q es la suma ponderada de K y L. La pendiente de la curva se puede calcular con la ayuda de la siguiente fórmula:
MPK = Q Q / K K = a
MPL = Q Q/L L = b
MRTS = MPL / MPK
MRTS = – b/a (b/a es constante)
Sin embargo, la isocuanta lineal no tiene existencia en el mundo real.
Isoquant en forma de L
Este es el caso de los complementos perfectos. En este contexto, la combinación entre capital y trabajo es en una proporción fija. Solo una combinación de mano de obra y capital es posible para producir un producto con una proporción fija de insumos.
Para aumentar la producción, una organización necesita aumentar ambos insumos proporcionalmente. La representación gráfica de la isocuanta de proporción de factor fijo tiene forma de L, mostrada en la Figura 5:
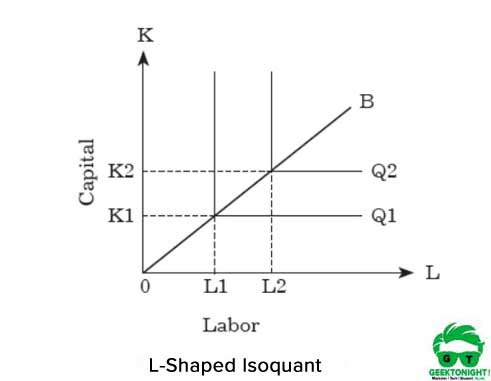
Como se muestra en la Figura 5, la isocuanta en forma de L representa que no hay sustitución entre trabajo y capital y se supone que son bienes complementarios. Se puede ver que se requieren unidades OK1 de capital y unidades OL1 de trabajo para la producción de Q1.
Por otro lado, para aumentar la producción de Q1 a Q2, una organización necesita aumentar los insumos de K1 a K2 y de L1 a L2 ambos. Esta relación entre capital y trabajo puede expresarse de la siguiente manera:
Q = f (K, L) = min (aK, bL)
donde, min implica Q igual a menor de los dos términos, aK y bL
Por ejemplo, en el caso de aK > bL, entonces Q = bL y en el caso de aK < bl, entonces, Q = aK.
Este isoquant es el mismo que la función de producción leontif.
Elasticidad de Sustitución Entre Factores
Sabemos que el MRTS es la pendiente de la isocuanta. Sin embargo, no revela el grado de sustituibilidad de un factor a otro. Es importante medir el grado de sustituibilidad entre las dos entradas.
Por lo tanto, los economistas han desarrollado una fórmula para estimar el grado de sustituibilidad entre los dos insumos, el capital y el trabajo, que se conoce como elasticidad de la sustitución de factores.
La elasticidad de sustitución de factores (σ) se refiere a la relación entre el cambio porcentual en la relación capital-trabajo y el cambio porcentual en los MRT.
Se representa matemáticamente de la siguiente manera:
σ = variación porcentual de la relación capital-trabajo/variación porcentual de los TMR
O,
σ = *
Si ∆K / L L = MR MRT ; σ = 1
Si ∆K/∆L > ∆MRT ; σ > 1
Si ∆K/∆L < ∆MRT ; σ < 1
Alta elasticidad de sustitución entre factores implica que los factores pueden ser fácilmente sustituidos el uno al otro, mientras que una baja elasticidad representa que la sustitución de los factores es posible hasta cierto punto.
En caso de isocuantas lineales, la elasticidad de sustitución sería infinita, y en caso de isocuantas en forma de L, sería cero.
Curvas de costes ISO
La curva de costes ISO es el locus de puntos de todas las diferentes combinaciones de trabajo y capital que una organización puede emplear, dado el precio de estos insumos. La línea de costo Iso representa el precio de los factores junto con la cantidad de dinero que una organización está dispuesta a gastar en factores.
En otras palabras, muestra diferentes combinaciones de factores que se pueden comprar con una cierta cantidad de dinero. La pendiente de la línea de costo iso depende de la relación entre el precio del trabajo y el precio del capital.
Por ejemplo, un productor tiene un presupuesto total de 1 120, que quiere gastar en los factores de producción, a saber, X e Y. El precio de X en el mercado es de ₹15 por unidad y el precio de Y es de ₹10 por unidad. La tabla 7.5 muestra las combinaciones:
| Combinaciones | Unidades de X | Unidades de Y | gasto Total |
|---|---|---|---|
| Un | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
El iso-costo de la línea se muestra en la Figura 7.8:
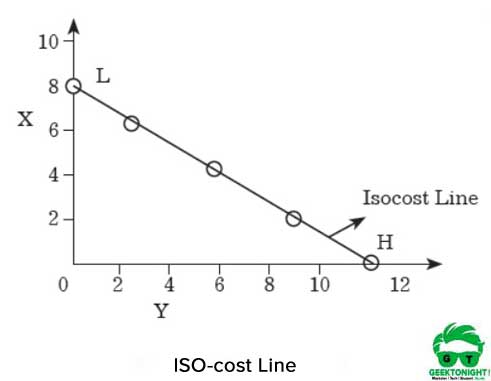
Como se muestra en la Figura 6, si el productor gasta la cantidad total de dinero para comprar X, entonces puede comprar 8 unidades de X. Por otro lado, si el productor compra Y con la cantidad total, entonces podría obtener 12 unidades.
Si los puntos H y L se unen en los ejes X e Y, respectivamente, se obtiene una línea recta, que se denomina línea de costo iso. Todas las combinaciones de X e Y que se encuentran en esta línea, tendrían la misma cantidad de costo que es de 1 120.
Del mismo modo, otras líneas de costos iso se pueden trazar tomando un costo superior a 120, en caso de que el productor esté dispuesto a gastar más cantidad de dinero en los factores de producción.
Con la ayuda de líneas de costos isocuenciales e iso, un productor puede determinar el punto en el que los insumos producen el máximo beneficio al incurrir en un costo mínimo. Tal punto se denomina equilibrio del productor.
Leer También: Utilidad Cardinal y Ordinal
Tutorial de Economía Empresarial
(Haga clic en el tema para leer)
Continúa, Comparte artículo con Amigos
Leave a Reply