31 ACT Math formler du behøver at vide

Plane geometri

vinkler og linjer

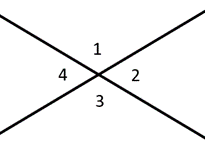
vinkler langs en linje kaldes supplerende vinkler, der tilføjer op til \(180^{\circ}\). Komplementære vinkler tilføje op til \(90^{\circ}\), en ret vinkel. Lodrette vinkler beskriver vinkler direkte overfor hinanden, som altid er kongruente. I diagrammet til venstre vil vi for eksempel sige, at vinkler 1 & 2 er supplerende, mens vinkler 1 & 3 er lodrette vinkler.

areal af en trekant

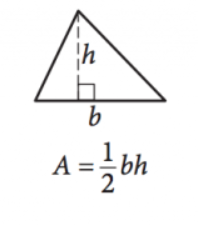
Billede venligst udlånt af SAT

\(\frac{1}{2}bh=a\)

denne ligning giver området \((A)\) af enhver trekant givet længder af basen \((b)\) og højde \((h)\). Bemærk, at højden er længden af linjen, der strækker sig i en komplementær vinkel fra enhver side (basen) op til punktet/vinklen direkte overfor den side.

for ligesidede trekanter, hvor alle tre sider \(s)\) har samme længde, er arealligningen:

\(\frac{s^2 \ kvm{3}}{4}=A\)

Pythagoras sætning

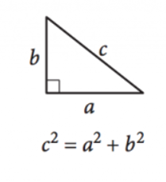
Billede venligst udlånt af SAT

da vinkler i en trekant altid tilføjer op til \(180^{\circ}\), defineres en højre trekant som enhver trekant med en ret vinkel, hvilket sikrer, at de to andre vinkler er komplementære. Sidelængderne på højre trekanter kan defineres af Pythagoras sætning:

\(a^2 + b^2=c^2\)

her er \(A\) og \(b\) længderne af benene eller siderne på tværs af de komplementære vinkler, og \(c\) er længden af hypotenusen, siden på tværs fra den rigtige vinkel.

det kan være nyttigt at også huske følgende Pythagoras tredobler eller værdier for sidelængder \((a, b, c)\): 3-4-5, 5-12-13, 7-24-25, og 8-15-17. Bemærk, at hypotenusen altid er den længste side.

specielle højre trekanter

der er to typer specielle højre trekanter, som har vinklerne og længdeforholdene som følger:

Billede venligst udlånt af SAT

områder af firkanter

\(a = lv\)

denne formel giver arealet af et rektangel med længde \(l\) og bredde \(v\).

\(a = bh\)

denne formel giver arealet af et parallelogram givet base \(b\) , længden af de længste sider og højden \(h\), defineret som længden af linjen, der strækker sig i en komplementær vinkel op fra den ene base til den anden.

\(a=\frac{b_1 + b_2}{2}\: \ gange\:h\)

denne formel giver området af en trapesformet med baser \(b_1\) og \(b_2\) og højde \(h\), defineret på samme måde som for parallelogrammer.

indvendige vinkler af regelmæssige polygoner

\((n-2)\:\times\:180^{\circ}= S\)

i en regelmæssig polygon, hvor alle sider og vinkler er ens, giver denne formel Summen \(S)\) af de indvendige vinkler givet en polygon med \(n\) sider og vinkler. Vi kan også finde hver indvendig vinkel ved at beregne \(\frac{S}{n}\).

bue længde i en cirkel

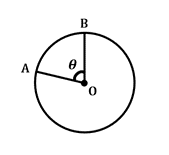
\(\frac {\theta}{360^{\circ}}\: \ gange\:2 \ pi r=bue\: længde\)

denne formel definerer længden af buen eller sektionen af cirkelomkredsen mellem to givne radier, der skærer i cirkelcentret med central vinkel \(\theta\). Bemærk, at \(2 \ pi r\) inkorporerer cirkelomkreds i denne formel.

Sektorområde i en cirkel

\(\frac{\Theta}{360^{\circ}}\:\times\:\pi r^2 = sektor\:område\)

i lighed med buelængde tilvejebringer denne formel området for sektoren mellem to givne radier, der skærer i cirkelcentret med central vinkel . \(\Pi r^2\) inkorporerer cirkelområde i denne formel.

3D-former

\(SA = 2 (LV + HV + lh)\)

\(V= LVH\)

disse formler giver overfladearealet \((SA)\) og volumen \((V)\) for et rektangulært prisme med længde \(l\), bredde \(B\) og højde \(h\).

\(V=\pi r^2h\)

dette er volumenformlen for en højre cylinder med basisradius \(r\) og højde \(h\).

hvis du har brug for overfladearealet eller volumenformlerne for andre 3D-figurer, vil ACT give relevante formler i selve spørgsmålene.

Trigonometri

SOH-CAH-TOA

de fleste ACT trig-problemer involverer manipulation af sinus, cosinus og tangent, som beregnes som følger for en given vinkel \(H\) i en højre trekant:

\(sin(h)=\frac{modsat\:ben}{hypotenuse}\)

\(cos (h)=\frac{tilstødende\: ben}{hypotenuse}\)

\(tan (s)=\frac{modsat\: ben}{tilstødende\: ben}=\frac{sin (s)} {cos (s)}\)

SOH-CAH-TOA er en nem huskeregel for at huske, hvilken trig funktion svarer til hvilke sidelængder!

Cofunktionsidentiteter

\(sin(s) = cos (90^{\circ} – s)\)

\(cos (h) = sin (90^{\circ} – h)\)

i ord viser disse identiteter, at en trig-funktion af vinkel \(H\) er lig med værdien af cofunktionen af komplementet af \(H\). De bruges generelt, når man beskæftiger sig med mere avanceret trigonometri, hvilket giver mulighed for nemme konverteringer mellem sinus og cosinus.

Ratio / gensidige Trig-identiteter

du kan lejlighedsvis se de gensidige identiteter af \(sin(s)\), \(cos (s)\) og \(tan (S)\), som er:

\(csc (s) =\frac{1}{sin(S)}\)

\(sek (k) =\frac{1}{cos (k))}\)

\(cot (s) =\frac{1}{tan (s)}\)

Pythagoras identitet

\(sin^2(s) + cos^2 (s)=1\)

baseret på Pythagoras sætning og enhedscirklen bruges denne identitet generelt sammen med cofunktionsidentiteterne til at løse trig-problemer (sans-lommeregner) hvor vinkel \(H\) eller værdierne for disse trig-funktioner i \(H\) er ukendte.

statistik og sandsynlighed

procenter

\(n\% \:af\:m = \frac{n}{100}\:\gange\:m\)

procenter bruges til at udtrykke dele af en helhed, og symbolet \(\%\) betyder generelt “divider med 100.”Som sådan svarer ovenstående ligning ethvert problem, der beder om \(n\%\) af mængde \(m\).

gennemsnit, Median, tilstand og rækkevidde

loven tester grundlæggende statistisk viden, der generelt involverer nedenstående foranstaltninger:

• middelværdi er gennemsnittet, eller \(\frac{sum\: of\: all\: terms}{total\: number\: of\:udtryk}\)
• Median er midtbegrebet, eller gennemsnittet af de to mellembegreber, hvis der er et lige antal udtryk
• Mode er det eller de udtryk, der forekommer hyppigst
• rækkevidde er forskellen mellem de største og mindste udtryk

Sandsynlighed

\(P(A) = \frac{nummer\:af\:ønsket\:resultater}{total\:antal\:af\:mulig\:resultater}\)

sandsynlighed repræsenterer sandsynligheden for, at en begivenhed \((a)\) forekommer, beregnet ved at dividere antallet af ønskede resultater med antallet af samlede mulige resultater. For eksempel er sandsynligheden for at rulle en 6 på en lige sidet terning \(\frac{1}{6}\).

uafhængige begivenheder

\(P(A\:og\:B) = P(A)\:\gange\:P(B)\)

begivenheder \(A\) og \(B\) er uafhængige, hvis \(A\) forekommende ikke påvirker sandsynligheden for \(B\) forekommende. For at beregne sandsynligheden for, at begge uafhængige begivenheder vil forekomme, multiplicerer vi deres individuelle sandsynligheder sammen. For eksempel er sandsynligheden for at vende hoveder to gange \(\frac{1}{2}\:\gange\:\frac{1}{2}=\frac{1}{4}\).

indpakning det op

vi har dækket masser af formler i dette indlæg, men sørg for også at gennemgå alle matematiske begreber gennem Algebra II og geometri! For eksempel kan du forvente, at komplekse tal, vektorer, matricer, ligningssystemer og manipulering af grafiske funktioner også er på testen. Se denne fulde beskrivelse af ACT math Sektionen for mere info.

Husk, at praksis gør mester, især for matematik! Du vil gerne prøve mange forskellige problemer før testdagen med det mål at virkelig forstå, hvordan du anvender og integrerer disse begreber og formler rettidigt.

da du har tilladelse til en lommeregner til handlingen, vil vi anbefale at bringe en, men med et forsigtighedsord. Husk, at ethvert matematikproblem kan løses uden en lommeregner, og det er let at spilde værdifuld tid ved at bruge din lommeregner, når du faktisk ikke har brug for det. Som sådan skal du udføre tidsbestemte øvelsesafsnit med din lommeregner, hvis du planlægger at medbringe en, og husk, at den kun er der som en sidste udvej: for at lette beregninger og øge din hastighed. Nå ud til det sjældent, og kontroller, at din specifikke model er tilladt i henhold til ACT calculator-politikken.