Isokvant kurve: Definition, egenskaber, typer, antagelser
Hvad er Isokvant kurve?
Isokvantkurve: en teknisk relation, der viser, hvordan input konverteres til output, er afbildet af en isokvantkurve. Det viser de optimale kombinationer af faktorindgange ved hjælp af priser på faktorindgange og deres mængder, der bruges til at producere den samme produktion.
udtrykket ISO indebærer lige og kvant betyder mængde eller output.
for eksempel anvendes 90 kapitalenheder og 10 arbejdsenheder til fremstilling af 100 kalendere.
Isokvantkurver kaldes også som lige produktkurver eller Produktions ligegyldighedskurver.
definition af Isokvantkurve
antagelser om Isokvantkurve
antagelserne om en isokvantkurve er som følger:
- der er kun to faktorer input, arbejdskraft og kapital, til at producere et bestemt produkt.
- kapital, arbejdskraft og varer er delelige i naturen.
- kapital og arbejdskraft er i stand til at erstatte hinanden op til en vis grænse.
- produktionsteknologi gives over en periode.
- produktionsfaktorer anvendes med fuld effektivitet.
lad os lære isokvant ved hjælp af følgende tabel.
tabel 1 viser de forskellige kombinationer af to faktorinput, nemlig arbejdskraft og kapital til produktion af 150 tons produktion:
| arbejdskraft | kapital |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
Figur 1 viser isokvantkurven for forskellige arbejdskapitalkombinationer, der hjælper med at producere 150 tons produktion:
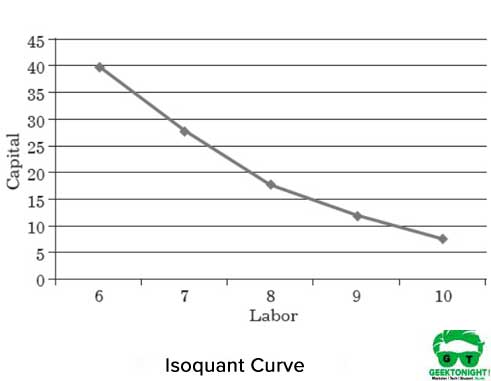
egenskaber ved Isokvantkurve
nogle af egenskaberne ved isokvantkurve er som følger:
- Isokvantkurver hældning nedad
- Isokvantkurver er konvekse til oprindelse
- Isokvantkurver kan ikke krydse hinanden
- højere isokvant, jo højere output

Isokvantkurver skråner nedad
det indebærer, at hældningen af isokvantkurven er negativ. Dette skyldes, at når kapitalen (K) øges, reduceres arbejdskraftmængden (L) eller omvendt for at holde det samme produktionsniveau.
Isokvantkurver er konvekse til oprindelse
det indebærer, at faktorindgange ikke er perfekte erstatninger. Denne egenskab viser substitution af input og faldende marginalrate for teknisk substitution af isokvant. Den marginale Betydning af et input (kapital) i form af et andet input (arbejde) mindskes sammen med den isokvante kurve.
figur 2 viser den konvekse isokvantkurve:
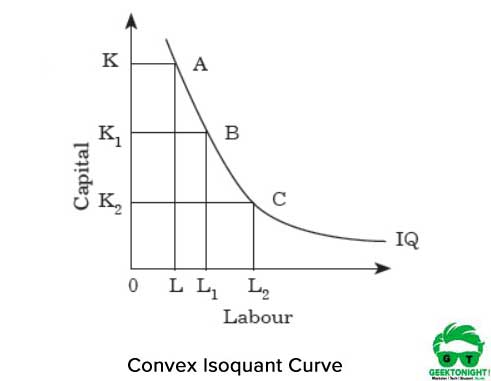
konveksiteten repræsenterer, at MRT ‘ erne mindskes, hvis vi bevæger os fra punkt A til B og fra B til C langs isokvanten. MRT ‘ erne mindskes, fordi de to input arbejdskraft og kapital ikke er perfekte erstatninger.
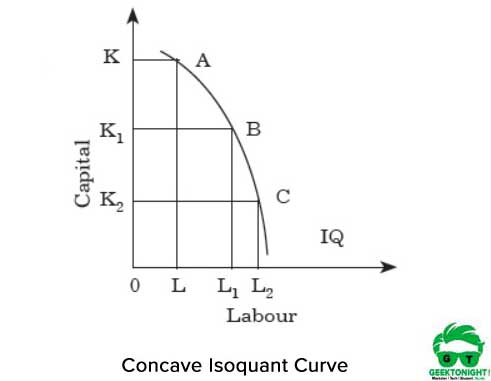
for hver stigning i arbejdskraft er der således et fald i kapitalen. Hvis isokvant er konkav, øges arbejdskraftens MRT for kapital. Figur 3 viser den konkave isokvantkurve:
som vist i figur 3, hvis vi bevæger os fra punkt A til B og fra B til C langs isokvanten, øges MRT ‘ erne. Det viser, at de to input arbejdskraft og kapital er perfekte erstatninger. For hver stigning i arbejdskraft er der således en stigning i kapitalen.
Isokvantkurver kan ikke krydse hinanden
en isokvant indebærer de forskellige niveauer af kombination, der producerer forskellige niveauer af input. Hvis isokvanterne skærer hinanden, ville det antyde, at en enkelt inputkombination kan producere to niveauer af output, hvilket ikke er muligt. Produktionsloven ville ikke være gældende.
højere isokvant jo højere output
det indebærer, at den højere isokvant repræsenterer højere output. Den øverste kurve af isokvanten producerer mere output end kurven nedenunder. Dette skyldes, at den større kombination af input resulterer i en større output sammenlignet med kurven, der er under den.
Marginalhastighed for teknisk Substitution
hældningen af isokvantkurven er den substitutionshastighed, der viser, hvordan en indgang kan erstattes med en anden, mens outputkonstanten holdes. Dette kaldes marginalrate for teknisk substitution (MRT ‘ er).
ifølge Lipsey kan “den marginale hastighed for teknisk substitution defineres som den hastighed, hvormed en faktor erstattes af en anden med output holdt konstant.”
formlen til beregning af MRT ‘ er er som følger:
MRTS = – kur K/kur L
hvor, kur K = Kapitalændring
kur L= arbejdskraftændring
formlen viser, at på et givet produktionsniveau ville MRTS af kapital til arbejde indebære den mængde arbejde, som virksomheden ville være villig til at opgive for en yderligere kapitalenhed. Tilsvarende ville MRT ‘ er af arbejdskraft for kapital indebære den mængde kapital, som virksomheden ville være villig til at opgive for en yderligere arbejdsenhed.
MRT ‘ er er også lig med forholdet mellem marginalprodukt af et input og det marginale produkt af et andet input. Udgangen langs isokvanten er konstant. Hvis ændringen i arbejdskraft erstattes af kapitalændringen, skal stigningen i produktionen som følge af stigning i arbejdskraft svare til faldet i produktionen som følge af fald i kapitalen. Matematisk
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Da output er uændret på et givet isoquant,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
Således kan vi sige, at MRTS mellem input er lig de marginale produkter af indgangene.
MRT ‘ erne beregnes som vist i tabel 2
| arbejdskraft | kapital | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
typer af Isokvantkurve
der er en kontinuerlig substitution af en inputvariabel med den anden inputvariabel med en faldende hastighed. Perfekte komplement og perfekte erstatninger giver forskellige former for isokvanter.
de forskellige typer isokvantkurve er som følger:
- lineær isokvant
- L – formet isokvant

lineær isokvant
det er en lige linje isokvant og repræsenterer en perfekt substituerbarhed mellem produktionsfunktionens input, kapital og arbejde. MRT ‘ er mellem input forbliver konstante. Figur 4 viser en lineær isokvant:
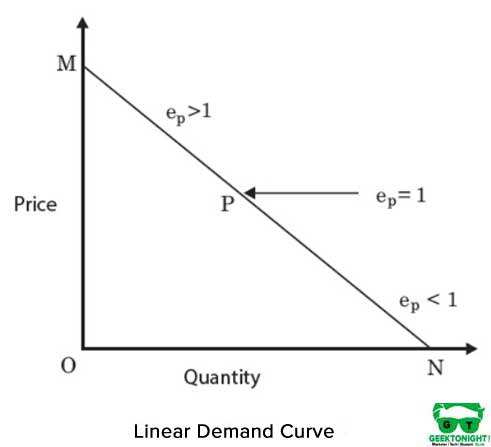
den algebraiske form for produktionsfunktion i tilfælde af lineær isokvant er som følger:
K = aK + BL
her er K den vægtede sum af K og L. kurvens hældning kan beregnes ved hjælp af følgende formel:
MPK = K / K = a
MPL = K / L = b
MRTS = MPL/MPK
MRTS = – b/A (b / A er konstant)
imidlertid har lineær isokvant ikke eksistens i den virkelige verden.
L-formet isokvant
dette er tilfældet med perfekte komplement. Under dette er kombinationen mellem kapital og arbejde i en fast andel. Kun en kombination af arbejdskraft og kapital er muligt at producere et produkt med anbragt andel af input.
for at øge produktionen skal en organisation øge begge input forholdsmæssigt. Den grafiske repræsentation af den faste faktorandel isokvant er L i form, vist i figur 5:
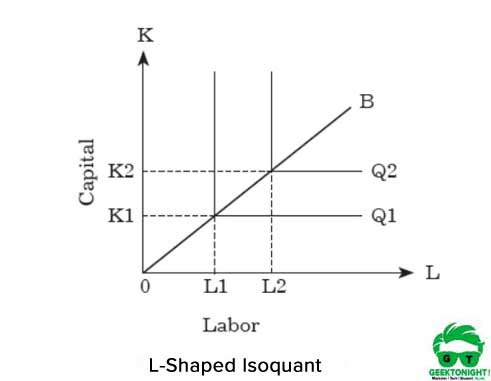
som vist i figur 5 repræsenterer den L-formede isokvant, at der ikke er nogen substitution mellem arbejde og kapital, og de antages at være komplementære varer. Det kan ses, at OK1-enheder af kapital og OL1-enheder af arbejdskraft er nødvendige for produktionen af 1.kvartal.
for at øge produktionen fra 1.kvartal til 2. kvartal skal en organisation på den anden side øge input fra K1 til K2 og L1 til L2 begge. Dette forhold mellem kapital og arbejde kan udtrykkes som følger:
K = F (K, L) = min (aK, bL)
hvor min indebærer K er lig med lavere af de to udtryk, aK og bL
for eksempel i tilfælde af aK > bL, derefter K = bL og i tilfælde aK < bL derefter, K = aK.
denne isokvant er den samme som leontif-produktionsfunktionen.
elasticitet af Substitution mellem faktorer
vi ved, at MRT ‘ er er hældningen af isokvanten. Det afslører imidlertid ikke graden af substituerbarhed af en faktor til en anden. Det er vigtigt at måle graden af substituerbarhed mellem de to indgange.
derfor har økonomer udviklet en formel til at estimere omfanget af substituerbarhed mellem de to input, kapital og arbejdskraft, der er kendt som elasticitet af faktorsubstitution.
elasticiteten af faktorsubstitution (kr) henviser til forholdet mellem den procentvise ændring i kapital-arbejdskraftforholdet og den procentvise ændring i MRT ‘ er.
det er matematisk repræsenteret på følgende måde:
liter = procentvis ændring i kapitalarbejdskvote/procentvis ændring i MRT
eller,
l = *
hvis L = L = L ; σ = 1
Hvis ∆K/∆L > ∆MRTS ; σ > 1
Hvis ∆K/∆L < ∆MRTS ; σ < 1
Høj elasticitet af substitution mellem faktorer, der indebærer, at de faktorer, der nemt kan erstattes af hinanden, mens en lav elasticitet angiver, at substitution af faktorer, der er muligt til en vis grad.
i tilfælde af lineær isokvant ville substitutionselasticiteten være uendelig, og i tilfælde af L-formede isokvanter ville den være nul.
ISO-Omkostningskurver
Iso-omkostningskurve er stedet for punkter for alle forskellige kombinationer af arbejdskraft og kapital, som en organisation kan anvende i betragtning af prisen på disse input. Iso-omkostningslinje repræsenterer prisen på faktorer sammen med det beløb, en organisation er villig til at bruge på faktorer.
det viser med andre ord forskellige kombinationer af faktorer, der kan købes til en vis mængde penge. Iso-omkostningslinjens hældning afhænger af forholdet mellem arbejdsprisen og kapitalprisen.
for eksempel har en producent et samlet budget på 120 kr., som han ønsker at bruge på produktionsfaktorerne, nemlig H. og Y. prisen på H. på markedet er 15 kr. pr. enhed, og prisen på Y er 10 kr. pr. enhed. Tabel 7.5 viser kombinationerne:
| kombinationer | enheder | enheder af Y | samlede udgifter |
|---|---|---|---|
| A | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
iso-omkostningslinjen er vist i figur 7.8:
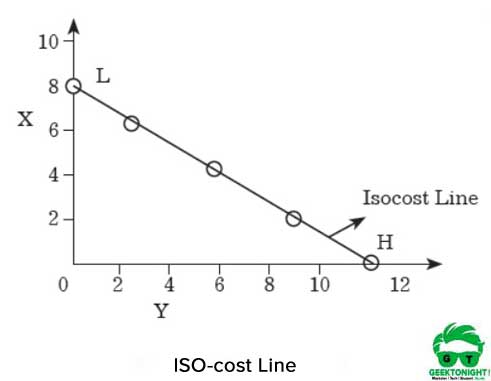
som vist i figur 6, hvis producenten bruger hele beløbet til at købe H, kan han/hun købe 8 enheder H. på den anden side, hvis producenten køber Y med hele beløbet, ville han / hun være i stand til at få 12 enheder.
hvis punkterne H og L er forbundet på henholdsvis H-og Y-akserne, opnås der en lige linje, som kaldes iso-cost-linje. Alle kombinationer af H og Y, der ligger på denne linje, ville have den samme mængde omkostninger, der er kr.120.
Tilsvarende kan andre iso-omkostningslinjer plottes ved at tage omkostninger mere end 120, hvis producenten er villig til at bruge mere penge på produktionsfaktorerne.
ved hjælp af isokvant-og iso-omkostningslinjer kan en producent bestemme det punkt, hvor input giver maksimal fortjeneste ved at pådrage sig minimumsomkostninger. Et sådant punkt betegnes som producentens ligevægt.
Læs Også: Kardinal og Ordinal Utility
Erhvervsøkonomi Tutorial
(Klik på emne for at læse)
Fortsæt, Del artikel med venner
Leave a Reply