31. Mathematische Formeln, die Sie kennen müssen

Ebene Geometrie

Winkel und Linien

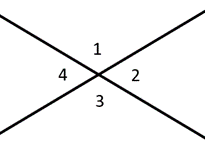
Winkel entlang einer Linie werden als Ergänzungswinkel bezeichnet und addieren sich zu \(180 ^{\circ}\). Komplementäre Winkel addieren sich zu \(90 ^{\circ}\), einem rechten Winkel. Vertikale Winkel beschreiben Winkel direkt gegenüber, die immer deckungsgleich sind. Im Diagramm links würden wir zum Beispiel sagen, dass die Winkel 1 & 2 vertikale Winkel sind, während die Winkel 1 & 3 vertikale Winkel sind.

Fläche eines Dreiecks

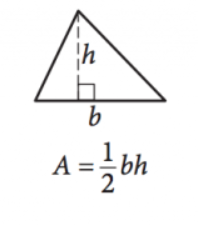
Bild mit freundlicher Genehmigung von SAT

\(\frac{1}{2}bh=A\)

Diese Gleichung liefert die Fläche \((A)\) eines Dreiecks mit den Längen der Basis \((b)\) und der Höhe \((h)\). Beachten Sie, dass die Höhe die Länge der Linie ist, die sich in einem komplementären Winkel von einer beliebigen Seite (der Basis) bis zu dem Punkt / Winkel direkt gegenüber dieser Seite erstreckt.

Für gleichseitige Dreiecke, bei denen alle drei Seiten \((s)\) gleich lang sind, lautet die Flächengleichung:

\(\frac{s^2\sqrt{3}}{4}=A\)

Satz des Pythagoras

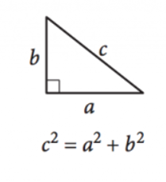
Bild mit freundlicher Genehmigung von SAT

Da sich Winkel in einem Dreieck immer zu \(180 ^{\circ}\) addieren, ist ein rechtwinkliges Dreieck als jedes Dreieck mit einem rechten Winkel definiert, wodurch sichergestellt wird, dass die anderen beiden Winkel komplementär sind. Die Seitenlängen von rechtwinkligen Dreiecken können durch den Satz des Pythagoras definiert werden:

\(a ^ 2 +b^2=c^2\)

Hier sind \(a\) und \(b\) die Längen der Beine oder die Seiten gegenüber den komplementären Winkeln, und \(c\) ist die Länge der Hypotenuse, die Seite gegenüber dem rechten Winkel.

Es kann hilfreich sein, sich auch die folgenden pythagoreischen Tripel oder Werte für Seitenlängen zu merken \((a, b, c)\): 3-4-5, 5-12-13, 7-24-25, und 8-15-17. Beachten Sie, dass die Hypotenuse immer die längste Seite ist.

Spezielle rechtwinklige Dreiecke

Es gibt zwei Arten von speziellen rechtwinkligen Dreiecken, die die folgenden Winkel- und Längenverhältnisse aufweisen:

Bild mit freundlicher Genehmigung von SAT

Flächen von Vierecken

\(A = lw\)

Diese Formel liefert die Fläche eines Rechtecks mit Länge \(l\) und Breite \(w \).

\(A = bh\)

Diese Formel liefert die Fläche eines Parallelogramms mit der Basis \(b\), der Länge der längsten Seiten und der Höhe \(h\), definiert als die Länge der Linie, die sich in einem komplementären Winkel von einer Basis zur anderen erstreckt.

\(A=\frac{b_1+b_2}{2}\:\)\:h\)

Diese Formel liefert die Fläche eines Trapezes mit Basen \(b_1\) und \(b_2\) und Höhe \(h\), definiert wie für Parallelogramme.

Innenwinkel von regulären Polygonen

\((n-2)\:\times\:180 ^ {\circ}= S\)

In einem regulären Polygon, in dem alle Seiten und Winkel gleich sind, liefert diese Formel die Summe \((S)\) der Innenwinkel bei einem Polygon mit \(n\) Seiten und Winkeln. Wir können auch jeden Innenwinkel finden, indem wir \(\frac{S}{n}\) berechnen.

Bogenlänge im Kreis

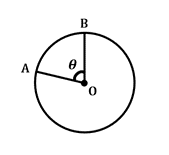
\(\ frac{\theta}{360^{\circ}}\:\Zeiten\:2\pi r=arc\:length\)

Diese Formel definiert die Länge des Bogens oder Abschnitts des Kreisumfangs zwischen zwei gegebenen Radien, die sich im Kreismittelpunkt mit dem Mittelwinkel \(\theta\) schneiden. Beachten Sie, dass \ (2\pi r\) den Kreisumfang in diese Formel einbezieht.

Sektorfläche in einem Kreis

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = Sektor\:Fläche\)

Ähnlich der Bogenlänge liefert diese Formel die Fläche des Sektors zwischen zwei gegebenen Radien, die sich im Kreismittelpunkt mit dem Mittelwinkel schneiden . Das \ (\pi r ^ 2\) enthält die Kreisfläche in diese Formel.

3D-Formen

\(SA = 2(lw + wh + lh)\)

\( V= lwh\)

Diese Formeln liefern die Oberfläche \((SA)\) und das Volumen \((V)\) für ein rechteckiges Prisma mit Länge \(l\), Breite \(w\) und Höhe \(h \).

\(V=\pi r^2h\)

Dies ist die Volumenformel für einen rechten Zylinder mit Basisradius \(r\) und Höhe \(h\).

Sollten Sie die Flächen- oder Volumenformeln für andere 3D-Formen benötigen, stellt das GESETZ relevante Formeln in den Fragen selbst zur Verfügung.

Trigonometrie

SOH-CAH-TOA

Die meisten ACT-Triggerprobleme beinhalten die Manipulation von Sinus, Cosinus und Tangens, die für einen gegebenen Winkel \ (x\) in einem rechtwinkligen Dreieck wie folgt berechnet werden:

\(sin(x)=\frac {Gegenteil\:Bein}{Hypotenuse}\)

\( cos(x)=\frac{angrenzend\:Bein}{hypotenuse}\)

\( tan(x)=\frac{gegenüberliegend\: Bein}{angrenzend\:bein}=\frac{sin(x)}{cos(x)}\)

SOH-CAH-TOA ist eine einfache Mnemonik, um sich zu merken, welche Triggerfunktion welchen Seitenlängen entspricht!

Cofunktionsidentitäten

\(sin(x) = cos(90^{\circ}-x)\)

\( cos(x) = sin(90^{\circ}-x)\)

In Worten zeigen diese Identitäten, dass eine Triggerfunktion des Winkels \(x\) gleich dem Wert der Cofunktion des Komplements von \(x\) ist. Sie werden im Allgemeinen verwendet, wenn es um fortgeschrittenere Trigonometrie geht, was eine einfache Konvertierung zwischen Sinus und Cosinus ermöglicht.

Verhältnis / Reziproke Triggeridentitäten

Gelegentlich können Sie die reziproken Identitäten von \(sin (x)\), \ (cos (x)\) und \ (tan (x)\) sehen, die:

\(csc(x) =\frac{1}{sin(x)}\)

\( sec(x) =\frac{1}{cos(x)}\)

\( cot(x) =\frac{1}{tan(x)}\)

Pythagoreische Identität

\(sin^2(x)+cos^2(x)=1\)

Basierend auf dem Satz des Pythagoras und dem Einheitskreis wird diese Identität im Allgemeinen neben den Kofunktionsidentitäten verwendet, um Triggerprobleme (ohne Rechner) zu lösen, bei denen der Winkel \ (x\) oder die Werte dieser Triggerfunktionen von \ (x\) unbekannt sind.

Statistik und Wahrscheinlichkeit

Prozentsätze

\(n\% \:von\:m = \frac{n}{100}\:\)\:m\)

Prozentsätze werden verwendet, um Teile eines Ganzen auszudrücken, und das Symbol \(\%\) bedeutet im Allgemeinen “dividieren durch 100.” Als solches beantwortet die obige Gleichung jedes Problem, das nach \(n \% \) der Menge \ (m \) fragt.

Mittelwert, Median, Modus und Bereich

Der ACT testet grundlegende statistische Kenntnisse, die im Allgemeinen die folgenden Maßnahmen umfassen:

• Mittelwert ist der Durchschnitt oder \(\frac{Summe\: von \: allen\: Termen} {Summe \: Anzahl \: von\:terme}\)
• Median ist der mittlere Term oder der Durchschnitt der beiden mittleren Terme, wenn es eine gerade Anzahl von Termen gibt
• Modus ist der Term, der am häufigsten vorkommt
• Range ist die Differenz zwischen dem größten und dem kleinsten Term

Probability

\(P(A) = \frac{number\ :of\:desired\:outcomes}{total\:number\:of\:possible\:outcomes}\)

Die Wahrscheinlichkeit stellt die Eintrittswahrscheinlichkeit eines Ereignisses \((A)\) dar, berechnet durch Division der Anzahl der gewünschten Ergebnisse durch die Anzahl der insgesamt möglichen Ergebnisse. Zum Beispiel ist die Wahrscheinlichkeit, eine 6 auf einem geraden Würfel zu würfeln, \(\frac{1}{6}\).

Unabhängige Ereignisse

\(P(A\:und\:B) = P(A)\:\times\:P(B)\)

Ereignisse \ (A\) und \(B\) sind unabhängig, wenn das Auftreten von \(A\) die Wahrscheinlichkeit des Auftretens von \(B\) nicht beeinflusst. Um die Wahrscheinlichkeit zu berechnen, dass beide unabhängigen Ereignisse auftreten, multiplizieren wir ihre individuellen Wahrscheinlichkeiten miteinander. Zum Beispiel ist die Wahrscheinlichkeit, dass Köpfe zweimal umgedreht werden, \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\) .

Einpacken

Wir haben viele Formeln in diesem Beitrag behandelt, aber achten Sie darauf, auch alle mathematischen Konzepte durch Algebra II und Geometrie zu überprüfen! Zum Beispiel können Sie erwarten, dass komplexe Zahlen, Vektoren, Matrizen, Gleichungssysteme und die Manipulation grafischer Funktionen ebenfalls auf dem Test sind. Weitere Informationen finden Sie in dieser vollständigen Beschreibung des Abschnitts ACT math.

Denken Sie daran, dass Übung den Meister macht, besonders für Mathematik! Sie möchten vor dem Testtag viele verschiedene Probleme ausprobieren, um wirklich zu verstehen, wie diese Konzepte und Formeln rechtzeitig angewendet und integriert werden können.

Da Ihnen ein Taschenrechner für die TAT erlaubt ist, empfehlen wir Ihnen, einen mitzubringen, jedoch mit einem Wort der Vorsicht. Denken Sie daran, dass jedes einfache mathematische Problem ohne Taschenrechner gelöst werden kann, und es ist einfach, wertvolle Zeit mit Ihrem Taschenrechner zu verschwenden, wenn Sie es eigentlich nicht brauchen. Üben Sie daher zeitgesteuerte Abschnitte mit Ihrem Taschenrechner, wenn Sie vorhaben, einen mitzubringen, und denken Sie daran, dass er nur als letzter Ausweg vorhanden ist: um Berechnungen zu erleichtern und Ihre Geschwindigkeit zu erhöhen. Greifen Sie selten danach und überprüfen Sie, ob Ihr spezifisches Modell gemäß der ACT Calculator-Richtlinie zulässig ist.