Isoquante Kurve: Definition, Eigenschaften, Typen, Annahmen
Was ist die isoquante Kurve?
Isoquante Kurve: Eine technische Beziehung, die zeigt, wie Eingaben in Ausgaben umgewandelt werden, wird durch eine isoquante Kurve dargestellt. Es zeigt die optimalen Kombinationen von Faktorinputs mit Hilfe von Preisen von Faktorinputs und deren Mengen, die verwendet werden, um den gleichen Output zu produzieren.
Der Begriff ISO impliziert gleich und quant bedeutet Menge oder Leistung.
Zum Beispiel werden für die Herstellung von 100 Kalendern 90 Einheiten Kapital und 10 Einheiten Arbeit verwendet.
Isoquante Kurven werden auch als Gleichproduktkurven oder Produktionsinfferenzkurven bezeichnet.
Definition der Isoquantenkurve
Annahmen der Isoquantenkurve
Die Annahmen einer Isoquantenkurve lauten wie folgt:
- Es gibt nur zwei Faktoren, Arbeit und Kapital, um ein bestimmtes Produkt herzustellen.
- Kapital, Arbeit und Güter sind ihrer Natur nach teilbar.
- Kapital und Arbeit können einander bis zu einer gewissen Grenze ersetzen.
- Technologie der Produktion wird über einen Zeitraum von Zeit gegeben.
- Produktionsfaktoren werden mit voller Effizienz genutzt.
Lernen wir Isoquant mit Hilfe der folgenden Tabelle.
Tabelle 1 zeigt die verschiedenen Kombinationen zweier Inputfaktoren, nämlich Arbeit und Kapital für die Erzeugung von 150 Tonnen Output:
| Arbeit | Kapital |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
Abbildung 1 zeigt die isoquante Kurve verschiedener Arbeitskapitalkombinationen, die zur Produktion von 150 Tonnen Output beitragen:
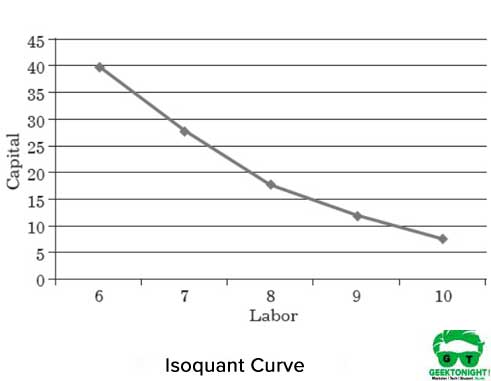
Eigenschaften der Isoquantenkurve
Einige der Eigenschaften der Isoquantenkurve sind wie folgt:
- Isoquante Kurven neigen sich nach unten
- Isoquante Kurven sind konvex zum Ursprung
- Isoquante Kurven können sich nicht schneiden
- Je höher die Isoquante, desto höher die Ausgabe

Isoquante Kurven neigen sich nach unten
Dies impliziert, dass die Steigung der isoquantenkurve negativ ist. Denn wenn das Kapital (K) vermehrt wird, verringert sich die Quantität der Arbeit (L) oder umgekehrt, um das gleiche Produktionsniveau zu erhalten.
Isoquante Kurven sind konvex zum Ursprung
Dies impliziert, dass Faktoreingaben keine perfekten Substitute sind. Diese Eigenschaft zeigt die Substitution von Inputs und abnehmende Grenzrate der technischen Substitution von Isoquant. Die marginale Bedeutung eines Inputs (Kapital) in Bezug auf einen anderen Input (Arbeit) nimmt mit der isoquanten Kurve ab.
Abbildung 2 zeigt die konvexe isoquante Kurve:
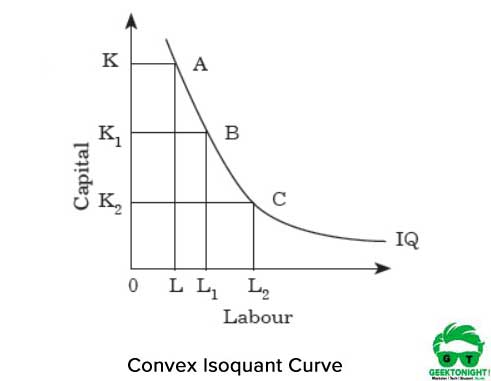
Die Konvexität stellt dar, dass die MRTS abnimmt, wenn wir uns entlang der Isoquanten von Punkt A nach B und von B nach C bewegen. Der MRTS nimmt ab, weil die beiden Inputs Arbeit und Kapital keine perfekten Substitute sind.
Für jede Zunahme der Arbeit gibt es also eine Abnahme des Kapitals. Wenn Isoquant konkav ist, erhöht sich der MRTS der Arbeit für Kapital. Abbildung 3 zeigt die konkave isoquante Kurve:
Wie in Abbildung 3 gezeigt, nimmt die MRTS zu, wenn wir uns entlang der Isoquante von Punkt A nach B und von B nach C bewegen. Es zeigt, dass die beiden Inputs Arbeit und Kapital perfekte Substitute sind. Für jede Zunahme der Arbeit gibt es also eine Zunahme des Kapitals.
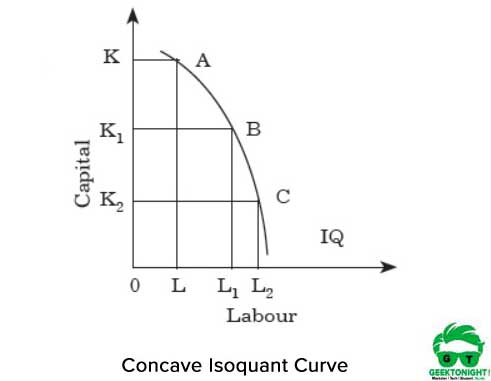
Isoquante Kurven können sich nicht schneiden
Eine Isoquante impliziert die verschiedenen Kombinationsebenen, die unterschiedliche Eingabeebenen erzeugen. Wenn sich die Isoquanten schneiden, würde dies bedeuten, dass eine einzelne Eingangskombination zwei Ausgabepegel erzeugen kann, was nicht möglich ist. Das Produktionsgesetz wäre nicht anwendbar.
Je höher die Isoquante, desto höher die Ausgabe
Dies bedeutet, dass die höhere Isoquante eine höhere Ausgabe darstellt. Die obere Kurve des Isoquanten erzeugt mehr Leistung als die darunter liegende Kurve. Dies liegt daran, dass die größere Kombination von Eingaben zu einer größeren Ausgabe im Vergleich zu der darunter liegenden Kurve führt.
Marginale Rate der technischen Substitution
Die Steigung der isoquantenkurve ist die Substitutionsrate, die zeigt, wie ein Eingang durch einen anderen ersetzt werden kann, während der Ausgang konstant gehalten wird. Dies wird als marginale Rate der technischen Substitution (MRTS) bezeichnet.
Laut Lipsey “kann die Grenzrate der technischen Substitution definiert werden als die Rate, mit der ein Faktor durch einen anderen ersetzt wird, wobei die Leistung konstant gehalten wird.”
Die Formel zur Berechnung der MRTS lautet wie folgt:
MRTS = – ∆K /∆L
wobei ∆K = Veränderung des Kapitals
∆L= Veränderung der Arbeit
Die Formel zeigt, dass MRTS des Kapitals für die Arbeit bei einem gegebenen Produktionsniveau die Menge an Arbeit implizieren würden, die das Unternehmen bereit wäre, für eine zusätzliche Kapitaleinheit aufzugeben. In ähnlicher Weise würden MRTS der Arbeit für Kapital die Menge an Kapital implizieren, die das Unternehmen bereit wäre, für eine zusätzliche Arbeitseinheit aufzugeben.
MRTS ist auch gleich dem Verhältnis des Grenzprodukts eines Inputs zum Grenzprodukt eines anderen Inputs. Die Ausgabe entlang der Isoquanten ist konstant. Wenn die Veränderung der Arbeit durch die Veränderung des Kapitals ersetzt wird, sollte die Zunahme der Produktion aufgrund der Zunahme der Arbeit mit der Abnahme der Produktion aufgrund der Abnahme des Kapitals übereinstimmen. Mathematisch
∆L x ZG= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Da die Leistung bleibt unverändert bei einem bestimmten isoquant,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
So, können wir sagen, dass MRTS zwischen den Eingängen gleich das randsortiment von den Eingängen.
Die MRTS wird wie in der Tabelle gezeigt berechnet 2
| Arbeit | Kapital | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
Typen der isoquanten Kurve
Es gibt eine kontinuierliche Substitution einer Eingangsvariablen durch die andere Eingangsvariable mit abnehmender Rate. Perfekte Ergänzungen und perfekte Substitute ergeben verschiedene Formen von Isoquanten.
Die verschiedenen Arten der isoquanten Kurve sind wie folgt:
- Lineares Isoquant
- L-förmiges Isoquant

Lineare Isoquante
Es ist eine gerade Isoquante und stellt eine perfekte Substituierbarkeit zwischen den Inputs, Kapital und Arbeit der Produktionsfunktion dar. MRTS zwischen den Eingängen bleibt konstant. Abbildung 4 zeigt eine lineare Isoquante:
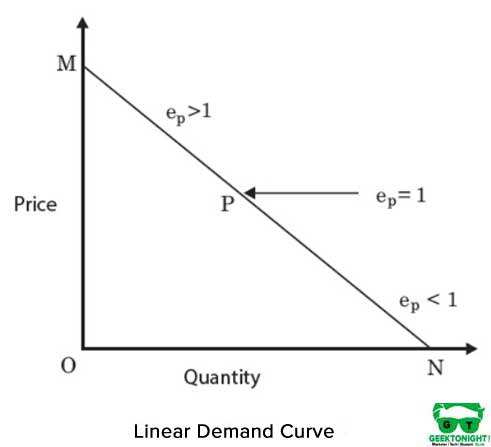
Die algebraische Form der Produktionsfunktion bei linearer Isoquante lautet wie folgt:
Q = aK + BL
Hier ist Q die gewichtete Summe von K und L. Die Steigung der Kurve kann mit Hilfe der folgenden Formel berechnet werden:
MPK = ∆Q /∆K = a
MPL = ∆Q /∆L = b
MRTS = MPL / MPK
MRTS = -b / a (b / a ist konstant)
Linear isoquant existiert jedoch nicht in der realen Welt.
L-förmiger Isoquant
Dies ist der Fall bei perfekten Ergänzungen. Unter diesem ist die Kombination von Kapital und Arbeit in einem festen Verhältnis. Nur eine Kombination von Arbeit und Kapital ist möglich, um ein Produkt mit festgelegtem Anteil an Inputs zu produzieren.
Um die Produktion zu steigern, muss eine Organisation beide Inputs proportional erhöhen. Die grafische darstellung der festen faktor anteil isoquant ist L in form, gezeigt in Abbildung 5:
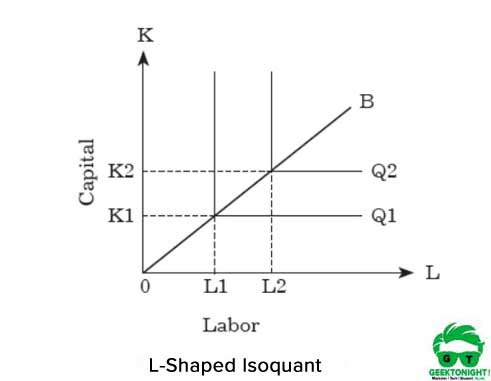
Wie in Abbildung 5 dargestellt, stellt die L-förmige Isoquante dar, dass es keine Substitution zwischen Arbeit und Kapital gibt und sie als komplementäre Güter angenommen werden. Es ist ersichtlich, dass für die Produktion von Q1 OK1 Kapitaleinheiten und OL1 Arbeitseinheiten benötigt werden.
Andererseits muss eine Organisation, um die Produktion von Q1 auf Q2 zu erhöhen, die Inputs von K1 auf K2 und L1 auf L2 erhöhen. Dieses Verhältnis zwischen Kapital und Arbeit kann wie folgt ausgedrückt werden:
Q = f (K, L) = min (aK, bL)
wobei min impliziert, dass Q dem unteren der beiden Terme aK und bL entspricht
Zum Beispiel im Fall aK > bL, dann Q = bL und im Fall aK < bL dann Q = aK.
Diese isoquant ist gleiche wie leontif produktion funktion.
Elastizität der Substitution zwischen Faktoren
Wir wissen, dass MRTS die Steigung der Isoquanten ist. Es zeigt jedoch nicht den Grad der Substituierbarkeit eines Faktors durch einen anderen. Es ist wichtig, den Grad der Substituierbarkeit zwischen den beiden Eingaben zu messen.
Daher haben Ökonomen eine Formel entwickelt, um das Ausmaß der Substituierbarkeit zwischen den beiden Inputs Kapital und Arbeit abzuschätzen, die als Elastizität der Faktorsubstitution bekannt ist.
Die Elastizität der Faktorsubstitution (σ) bezieht sich auf das Verhältnis der prozentualen Veränderung des Kapital-Arbeits-Verhältnisses zur prozentualen Veränderung der MRTS.
Es wird mathematisch wie folgt dargestellt:
σ = prozentuale Veränderung der Kapitalarbeitsverhältnisse /prozentuale Veränderung der MRTS
Oder,
σ = *
Wenn ∆K/∆L = ∆MRTS ; σ = 1
Wenn ∆K/∆L > ∆MRTS ; σ > 1
Wenn ∆K/∆L < ∆MRTS ; σ < 1
Hohe Elastizität der substitution zwischen den Faktoren bedeutet, dass die Faktoren, die können leicht ersetzt werden, um jedes andere, während eine geringe Elastizität bedeutet, dass die substitution der Faktoren ist möglich, zu einem gewissen Grad.
Bei linearen Isoquanten wäre die Substitutionselastizität unendlich und bei L-förmigen Isoquanten Null.
ISO-Kostenkurven
Die Iso-Kostenkurve ist der Ort der Punkte aller verschiedenen Kombinationen von Arbeit und Kapital, die eine Organisation angesichts des Preises dieser Inputs einsetzen kann. Die Iso-Kostenlinie repräsentiert den Preis von Faktoren zusammen mit dem Geldbetrag, den eine Organisation bereit ist, für Faktoren auszugeben.
Mit anderen Worten, es zeigt verschiedene Kombinationen von Faktoren, die zu einem bestimmten Geldbetrag gekauft werden können. Die Steigung der Iso-Kostenlinie hängt vom Verhältnis des Preises der Arbeit zum Preis des Kapitals ab.
Zum Beispiel hat ein Produzent ein Gesamtbudget von ₹120, das er für die Produktionsfaktoren X und Y ausgeben möchte. Der Preis von X auf dem Markt beträgt ₹15 pro Einheit und der Preis von Y beträgt ₹10 pro Einheit. Tabelle 7.5 zeigt die Kombinationen:
| Kombinationen | Einheiten von X | Einheiten von Y | Gesamtausgaben |
|---|---|---|---|
| A | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
Die ISO-Kostenlinie ist in Abbildung 7.8 dargestellt:
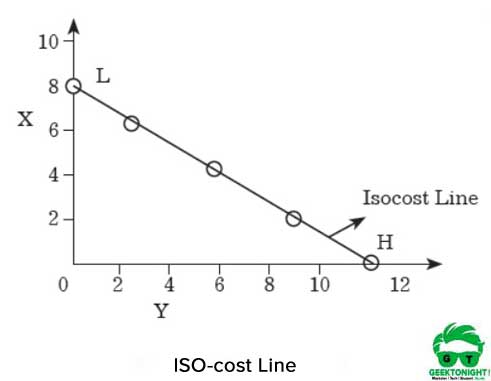
Wie in Abbildung 6 gezeigt, kann der Produzent, wenn er den gesamten Geldbetrag für den Kauf von X ausgibt, 8 Einheiten von X kaufen. Wenn der Produzent hingegen Y mit dem gesamten Betrag kauft, kann er 12 Einheiten erhalten.
Wenn die Punkte H und L auf der X- bzw. Y-Achse verbunden sind, wird eine gerade Linie erhalten, die als Iso-Kostenlinie bezeichnet wird. Alle Kombinationen von X und Y, die auf dieser Linie liegen, hätten die gleichen Kosten, die ₹120 sind.
In ähnlicher Weise können andere ISO-Kostenlinien gezeichnet werden, indem Kosten von mehr als 120 übernommen werden, falls der Hersteller bereit ist, mehr Geld für die Produktionsfaktoren auszugeben.
Mit Hilfe von Isoquanten- und Iso-Kostenlinien kann ein Produzent den Punkt bestimmen, an dem die Inputs den maximalen Gewinn bei minimalen Kosten erzielen. Ein solcher Punkt wird als Produzentengleichgewicht bezeichnet.
Lesen Sie auch: Kardinal und Ordinal Utility
Business Economics Tutorial
(Zum Lesen auf das Thema klicken)
Weiter, Artikel mit Freunden teilen
Leave a Reply