31 ACT Math kaavoja sinun tulee tietää

Tasogeometria

kulmat ja viivat

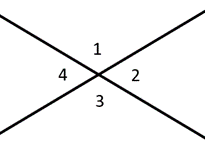
suoran suuntaisia kulmia kutsutaan täydentäviksi kulmiksi, joiden yhteenlasku on \(180^{\circ}\). Komplementtikulmiot lasketaan yhteen \(90^{\circ}\), joka on suora kulma. Pystykulmat kuvaavat suoraan toisiaan vastapäätä olevia kulmia, jotka ovat aina yhteneviä. Esimerkiksi vasemmalla olevassa kaaviossa sanotaan, että kulmat 1 & 2 ovat täydentäviä, kun taas kulmat 1 & 3 ovat pystykulmia.

kolmion pinta-ala

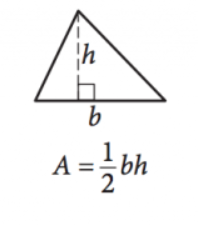
Kuva SAT

\(\frac{1}{2}bh=a\)

tämä yhtälö antaa alueen \((a)\) minkä tahansa kolmion annettujen pituuksien pituuksien \((b)\) ja korkeuden \((h)\). Huomaa, että korkeus on sen suoran pituus, joka ulottuu komplementaarisessa kulmassa miltä tahansa sivulta (jalustalta) suoraan vastapäätä olevaan pisteeseen/kulmaan asti.

Tasasivuisille kolmioille, joissa kaikki kolme sivua \((s)\) ovat samanpituisia, pinta-alan yhtälö on:

\(\frac{s^2\sqrt{3}}{4}=A\)

Pythagoraan lause

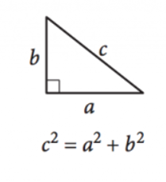
Kuva SAT

koska kulmat kolmion aina lisätä jopa \(180^{\circ}\), suorakulmainen kolmio määritellään mikä tahansa kolmio, jossa on yksi kulmassa, varmistaa kaksi muuta kulmat ovat toisiaan. Suorakulmaisten kolmioiden sivujen pituudet voidaan määritellä Pythagoraan lauseella:

\(a^2+B^2=c^2\)

tässä \(A\) ja \(b\) ovat jalkojen pituudet eli sivut vastakkain komplementaarisista kulmista, ja \(c\) on hypotenuusan pituus, oikeassa kulmassa olevan sivun pituus.

voi olla hyödyllistä opetella ulkoa myös seuraavat Pythagoraan tripletit eli sivujen pituuksien arvot \((a, b, c)\): 3-4-5, 5-12-13, 7-24-25, ja 8-15-17. Huomaa, että hypotenuusa on aina pisin sivu.

Erityisoikeuskolmioita

on kahdenlaisia erityisoikeuskolmioita, joiden kulma-ja pituussuhteet ovat seuraavat:

Kuva SAT

Quadrilateralsin alueet

\(A = lw\)

tällä kaavalla saadaan suorakulmion pinta-ala, jonka pituus on \(l\) ja leveys \(w\).

\(a = bh\)

tällä kaavalla saadaan annettavan parallelogrammin pinta-ala \(b\) , pisimpien sivujen pituus ja korkeus \(h\), jotka määritellään sen janan pituudeksi, joka ulottuu komplementaarisessa kulmassa yhdestä kannasta toiseen.

\(a = \frac{b_1+b_2}{2}\:\times\:h\)

tällä kaavalla saadaan puolisuunnikkaan pinta-ala, jonka emäkset \(b_1\) ja \(b_2\) sekä korkeus \(h\) määritellään samalla tavalla kuin parallelogrammeille.

säännöllisten monikulmioiden sisäkulmat

\((n-2)\:\times\:180^{\circ}= s\)

säännöllisessä monikulmiossa, jossa kaikki sivut ja kulmat ovat yhtä suuret, tämä kaava antaa monikulmiolle, jolla on \(n\) sivut ja kulmat, annettujen sisäkulmien summan \(s)\. Voimme myös löytää jokaisen sisäkulman laskemalla \(\frac{s}{n}\).

kaaren pituus ympyrässä

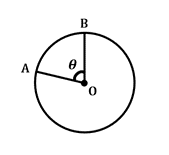
\(\frac {\theta}{360^{\circ}}\:\times\:2\pi r = arc\: length\)

tässä kaavassa määritellään kaaren eli ympyrän kehän osan pituus kahden annetun säteen välillä, jotka leikkaavat ympyrän keskipisteessä keskikulman \(\theta\). Huomaa, että \(2\pi r\) sisältää ympyrän kehän tähän kaavaan.

sektorin pinta-ala ympyrässä

\(\frac{\Theta}{360^{\circ}}\:\times\:\pi r^2 = sektori\:pinta-ala\)

samalla tavalla kuin kaaren pituus, tällä kaavalla saadaan sektorin pinta-ala kahden annetun säteen väliltä, jotka leikkaavat ympyrän keskipisteen keskuskulmalla . \ (\Pi r^2\) sisältää ympyrän alueen tähän kaavaan.

3D-muodot

\(SA = 2 (lw + wh + lh)\)

\(V= lwh\)

näillä kaavoilla saadaan suorakulmaisen prisman pinta-ala \((SA)\) ja tilavuus \((V)\), jonka pituus on \(l\), leveys \(w\) ja korkeus \(h\).

\(V=\pi r^2h\)

tämä on oikean sylinterin tilavuuskaava, jonka pohjan säde on \(r\) ja korkeus \(h\).

jos tarvitset pinta-ala-tai tilavuuskaavoja muille 3D-muodoille, laki antaa relevantit kaavat itse kysymyksissä.

Trigonometria

SOH-CAH-TOA

useimpiin NÄYTÖSKOLMION ongelmiin liittyy sinin, kosinin ja tangentin manipulointi, jotka lasketaan seuraavasti annetulle kulmalle \(x\) suorakulmaisessa kolmiossa:

\(sin(x)=\frac{opposite\: leg}{hypotenuusa}\)

\(cos (x) = \frac{adjacent\: leg}{hypotenuse}\)

\(tan (x) = \frac{opposite\: leg}{adjacent\: leg} = \frac{sin(x)}{cos (x)}\)

SOH-CAH-TOA on helppo muisto siitä, mikä trig-funktio vastaa mitä sivun pituuksia!

Cofunction Identities

\(sin(x) = cos (90^{\circ} – x)\)

\(cos(x) = sin(90^{\circ}-x)\)

sanoilla nämä identiteetit osoittavat, että kulman \(x\) trig-funktio on yhtä suuri kuin komplementin \(x\) yhteisfunktio. Niitä käytetään yleensä käsiteltäessä kehittyneempää trigonometriaa, mikä mahdollistaa helpon muunnoksen sinin ja kosinin välillä.

suhde / vastavuoroiset Trig-identiteetit

saatat joskus nähdä \(sin(x)\), \(cos(x)\), ja \(tan(x)\), jotka ovat:

\(csc (x) =\frac{1}{sin (x)}\)

\(sec (x) =\frac{1}{cos (x)}\)

\(cot (x) = \frac{1}{tan (x)}\)

pythagoralainen identiteetti

\(sin^2 (x)+cos^2 (x)=1\)

Pythagoraan lauseen ja yksikköympyrän perusteella tätä identiteettiä käytetään yleensä kofunktiodentiteettien rinnalla ratkaisemaan trig-ongelmia(sans calculator), joissa kulma \(x\) tai näiden \(x\) trig-funktioiden arvot ovat tuntemattomia.

tilastot ja todennäköisyys

prosentit

\(n\% \: of\: m = \frac{n}{100}\:\times\:M\)

prosenttilukuja käytetään ilmaisemaan kokonaisuuden osia, ja \ ( \ % \ ) – Symboli tarkoittaa yleensä “Jaa 100: lla.”Sellaisenaan yllä oleva yhtälö vastaa kaikkiin ongelmiin, joissa pyydetään \(n\%\) määrää \(m\).

keskiarvo, mediaani, moodi ja vaihteluväli

ACT testaa tilastollista perustietoa, johon yleensä kuuluvat seuraavat mittarit:

• keskiarvo on keskiarvo, tai \(\frac {sum\: of\: all\: terms} {total\: number\: of\:termit}\)
• mediaani on keskimmäinen termi, tai kahden keskimmäisen termin keskiarvo, jos on parillinen määrä termejä
• Mode on termi(s), joka esiintyy useimmin
• vaihteluväli on suurimman ja pienimmän termin ero

todennäköisyys

\(P(A) = \frac{numero\:of\:despected\:outcomes}{total\:number\:of\:possible\:outcomes}\)

todennäköisyys tarkoittaa tapahtuman \((a)\) toteutumisen todennäköisyyttä, joka lasketaan jakamalla toivottujen lopputulosten lukumäärä mahdollisten kokonaistulosten lukumäärällä. Esimerkiksi todennäköisyys heittää 6 parillisella nopalla on \(\frac{1}{6}\).

riippumattomat tapahtumat

\(P (A\: and\: B) = P(A)\:\times\: P(B)\)

tapahtumat \(A\) ja \(b\) ovat riippumattomia, jos \(a\) esiintyminen ei vaikuta \(B\) esiintymisen todennäköisyyteen. Laskemme todennäköisyyden, että molemmat riippumattomat tapahtumat tapahtuvat, kertomalla niiden yksittäiset todennäköisyydet yhdessä. Esimerkiksi todennäköisyys kääntää päitä kahdesti on \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

Waping It Up

we ‘ ve covered lot of forms in this post, but be much to also review all math concepts through Algebra II and Geometry! Esimerkiksi kompleksilukujen, vektorien, matriisien, yhtälöiden järjestelmien ja graafisten funktioiden manipuloinnin voi olettaa olevan myös testissä. Katso tämä täydellinen kuvaus ACT math osiossa lisätietoja.

muista, että harjoittelu tekee mestarin, varsinkin matematiikassa! Ennen testipäivää kannattaa kokeilla paljon erilaisia ongelmia, joiden tavoitteena on todella ymmärtää, miten näitä käsitteitä ja kaavoja voidaan soveltaa ja integroida oikea-aikaisesti.

koska laskimen saa esittää, neuvoisimme tuomaan sellaisen, mutta varoituksen sanalla. Muista, että jokainen ACT matematiikka ongelma voidaan ratkaista ilman Laskin, ja se on helppo tuhlata arvokasta aikaa käyttämällä laskin, kun todella ei tarvitse. Sinällään, tee ajastettu käytäntö osiot laskimella, jos aiot tuoda yhden, ja muista, että se on vain siellä viimeisenä keinona: helpottaa laskelmia ja lisätä nopeutta. Reach sitä harvoin, ja tarkista, että erityinen malli on sallittu per teko laskin politiikkaa.