Isoquant-käyrä: määritelmä, ominaisuudet, tyypit, oletukset
mikä on Isoquant-käyrä?
Isokanttikäyrä: tekninen suhde, joka osoittaa, miten tulot muunnetaan tuotokseksi, kuvataan isokanttikäyrällä. Siinä esitetään tuotannontekijäpanosten optimaaliset yhdistelmät saman tuotoksen tuottamiseen käytettävien tuotannontekijäpanosten hintojen ja niiden määrien avulla.
termi ISO merkitsee yhtä ja kvantti tarkoittaa määrää tai tuotosta.
esimerkiksi 100 kalenterin tuottamiseen käytetään 90 pääoma-ja 10 työyksikköä.
Isokanttikäyriä kutsutaan myös yhtäsuuriksi tuotekäyriksi tai tuotannon välinpitämättömyyskäyriksi.
Isokanttikäyrän määritelmä
Isokanttikäyrän oletukset
isokanttikäyrän oletukset ovat seuraavat:
- tietyn tuotteen tuottamiseen on vain kaksi tuotantopanosta, työ ja pääoma.
- pääoma, työ ja tavarat ovat luonteeltaan jaollisia.
- pääoma ja työ voivat korvata toisensa tiettyyn rajaan asti.
- tuotantotekniikka on annettu ajan kuluessa.
- tuotannontekijöitä käytetään täydellä teholla.
opetellaan isoquant seuraavan taulukon avulla.
taulukossa 1 esitetään kahden tuotantopanoksen, työn ja pääoman, erilaiset yhdistelmät 150 tonnin tuotannon tuottamiseksi:
| Työvoima | pääoma |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
kuviossa 1 esitetään työvoimapääoman eri yhdistelmien isoquanttikäyrä, joka auttaa tuottamaan 150 tonnia tuotosta:
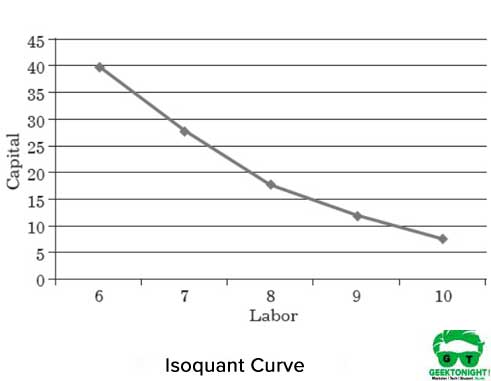
Isokanttikäyrän ominaisuudet
jotkin isokanttikäyrän ominaisuudet ovat seuraavat:
- Isokanttikäyrät kaltevuus alaspäin
- Isokanttikäyrät ovat kuperia origoon
- isokanttikäyrät eivät voi leikkautua keskenään
- suurempi isokantti mitä suurempi ulostulo

Isoquant-käyrä kaltevuus alaspäin
se viittaa siihen, että isoquant-käyrän kaltevuus on negatiivinen. Tämä johtuu siitä, että kun pääomaa (K) lisätään, työn määrä (L) vähenee tai päinvastoin, jotta tuotannon taso pysyisi samana.
Isoquanttikäyrät ovat kuperia alkuperään
nähden, mikä viittaa siihen, että tekijätulot eivät ole täydellisiä korvikkeita. Tämä ominaisuus osoittaa tuotantopanosten korvaamisen ja isokantin teknisen korvaamisen vähenevän marginaaliasteen. Yhden panoksen (pääoman) marginaalinen merkitys suhteessa toiseen panokseen (työhön) pienenee isokanttikäyrän myötä.
kuvassa 2 esitetään Kupera isokanttikäyrä:
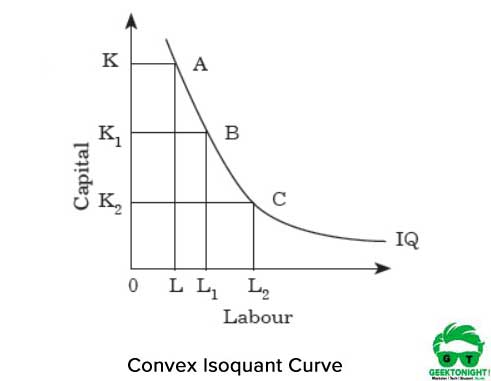
convexity tarkoittaa, että MRTS pienenee, jos siirrymme pisteestä A pisteeseen B ja B pisteeseen C pitkin isoquant. MRTS vähenee, koska kaksi panosta työ ja pääoma eivät ole täydellisiä korvikkeita.
näin ollen jokaista työn lisäystä kohden pääoma vähenee. Jos isoquant on koverrettu, työn MRTs pääomalle kasvaa. Kuvassa 3 on kovera isokanttikäyrä:
kuten kuvassa 3 on esitetty, jos siirrymme pisteestä A pisteeseen B ja B: stä C isokanttia pitkin, MRTS kasvaa. Se osoittaa, että nämä kaksi panosta työ ja pääoma ovat täydellisiä korvikkeita. Näin ollen jokaista työn lisäystä kohti pääoma lisääntyy.
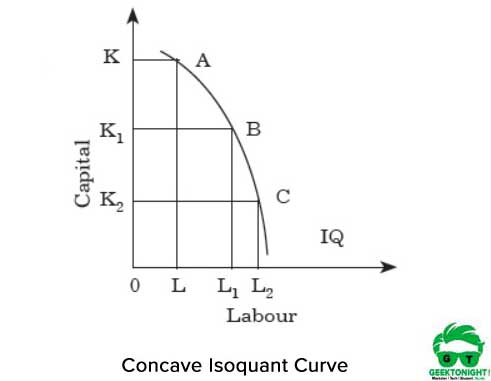
Isokanttikäyrät eivät voi leikkauttaa toisiaan
Isokantti tarkoittaa, että yhdistelmätasot tuottavat eri tulotasoja. Jos isokantit leikkaavat toisensa, se tarkoittaisi, että yhdellä tuloyhdistelmällä voidaan tuottaa kaksi lähtötasoa, mikä ei ole mahdollista. Tuotantolakia ei sovellettaisi.
suurempi isoquantti mitä suurempi tuotos
merkitsee sitä, että mitä suurempi isoquantti edustaa korkeampaa tuotosta. Isokvantin yläkäyrä tuottaa enemmän ulostuloa kuin alla oleva käyrä. Tämä johtuu siitä, että suurempi yhdistelmä panos johtaa suurempi lähtö verrattuna käyrä, joka on sen alapuolella.
teknisen substituution Marginaalinopeus
isokanttikäyrän kulmakerroin on substituutionopeus, joka osoittaa, miten yksi tulo voidaan korvata toisella samalla kun lähtövakio pidetään. Tätä kutsutaan tekniseksi korvausasteeksi (marginal rate of technical substitution, MRTS).
Lipseyn mukaan “teknisen substituution marginaalinopeus voidaan määritellä nopeudeksi, jolla yksi tekijä korvautuu toisella tuotoksen pysyessä vakiona.”
MRTs: n laskukaava on seuraava:
MRTS = – ∆K/∆L
jossa ∆k = pääoman muutos
∆l= työn muutos
kaavasta käy ilmi, että tietyllä tuotantotasolla työn pääoman MRTS merkitsisi sitä työmäärää, josta yritys olisi valmis luopumaan lisäpääomayksikköä varten. Vastaavasti työvoiman MRTS pääomalle tarkoittaisi sitä pääoman määrää, josta yritys olisi valmis luopumaan lisätyöyksikön vuoksi.
MRTS on myös yhtä suuri kuin yhden panoksen marginaalituotteen suhde toisen panoksen marginaalituotteeseen. Ulostulo isokvanttia pitkin on vakio. Jos työn muutos korvataan pääoman muutoksella, työn lisääntymisestä johtuvan tuotannon kasvun pitäisi vastata pääoman vähenemisestä johtuvaa tuotannon vähenemistä. Matemaattisesti
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
koska lähtö pysyy muuttumattomana tietyssä isoquantissa,
∆l x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
mrtskl = (MPL / MPK)
näin voidaan sanoa, että MRTs panosten välillä on yhtä suuri kuin panosten Marginaalituotteet.
MRTS lasketaan taulukon mukaisesti 2
| Työvoima | pääoma | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
Isokanttikäyrän tyypit
yksi input-muuttuja korvataan jatkuvasti toisella input-muuttujalla vähenevällä nopeudella. Täydelliset täydennykset ja täydelliset korvikkeet antavat erilaisia isokanteja.
isokvanttikäyrän eri tyypit ovat seuraavat:
- Lineaarinen isokantti
- L-muotoinen isokantti

Lineaarinen isokantti
se on suora isokantti ja edustaa täydellistä korvattavuutta tuotantofunktion panosten, pääoman ja työn välillä. MRTS syötteiden välillä pysyy vakiona. Kuvassa 4 esitetään lineaarinen isokantti:
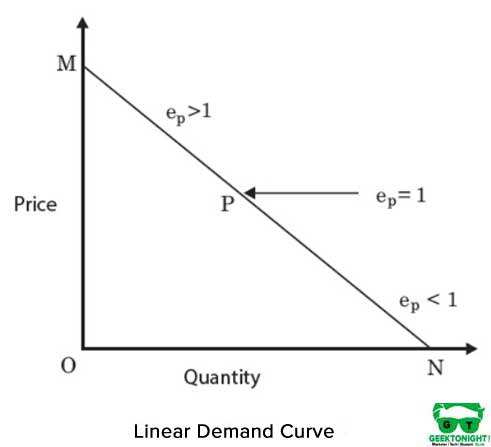
algebrallinen tuotantofunktion muoto lineaarisen isoquantin tapauksessa on seuraava:
Q = aK + BL
tässä Q on K: n ja L: n painotettu summa. käyrän kulmakerroin voidaan laskea seuraavan kaavan avulla:
MPK = ∆Q/∆K = A
mpl = ∆Q/∆L = B
MRTS = MPL / MPK
MRTS = – b/A (b/A on vakio)
lineaarista isokanttia ei kuitenkaan ole olemassa reaalimaailmassa.
L: n muotoinen isokantti
tämä koskee täydellisiä täydennyksiä. Tässä pääoman ja työn yhdistelmä on kiinteässä suhteessa. Vain yhdellä työn ja pääoman yhdistelmällä on mahdollista tuottaa tuote, johon on kiinnitetty tietty osuus panoksia.
tuotannon lisäämiseksi organisaation on lisättävä molempia panoksia samassa suhteessa. Kiinteän tekijän osuuden isoquantin graafinen esitys on L: n muotoinen, kuvassa esitetty 5:
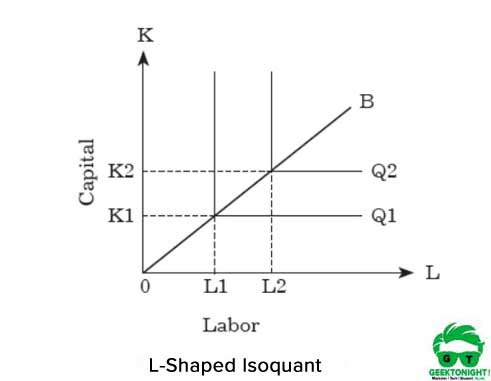
kuten kuviosta 5 ilmenee, L: n muotoinen isokantti merkitsee sitä, että työn ja pääoman välillä ei ole korviketta, ja niiden oletetaan olevan toisiaan täydentäviä tavaroita. Voidaan nähdä, että Q1: n tuottamiseen tarvitaan OK1 pääomayksikköä ja OL1 työvoimayksikköä.
toisaalta tuotannon kasvattamiseksi Q1: stä Q2: een organisaation on lisättävä panoksia K1: stä K2: een ja L1: stä L2: een molempiin. Tämä pääoman ja työn välinen suhde voidaan ilmaista seuraavasti:
Q = f (K, L) = min (aK, bL)
jossa min merkitsee Q yhtä kuin pienempi kahdesta termistä, aK ja bL
esimerkiksi jos aK > bL, niin Q = bL ja jos ak < bL sitten, Q = aK.
tämä isokantti on sama kuin leontifunktio.
tekijöiden välisen substituution kimmoisuus
tiedämme, että MRTS on isokvantin kulmakerroin. Se ei kuitenkaan paljasta, missä määrin tekijä on korvattavissa toisella. On tärkeää mitata, missä määrin nämä kaksi panosta ovat korvattavissa.
siksi taloustieteilijät ovat kehittäneet kaavan, jolla voidaan arvioida kahden panoksen, pääoman ja työn, välisen korvattavuuden laajuutta.
tekijän substituution Elastisuudella (σ) tarkoitetaan pääoman ja työvoiman välisen suhteen prosentuaalisen muutoksen suhdetta MRTS-arvon prosenttimuutokseen.
se esitetään matemaattisesti seuraavasti:
σ = pääomatyövoiman prosentuaalinen muutos / MRT: n prosentuaalinen muutos
tai,
σ = *
if ∆K / ∆L = ∆MRTS ; σ = 1
If ∆K/∆L > ∆MRTS ; σ > 1
if ∆K / ∆L < ∆MRTS ; σ < 1
tekijöiden välisen substituution suuri elastisuus merkitsee sitä, että tekijät voidaan helposti korvata keskenään, kun taas alhainen elastisuus merkitsee sitä, että tekijöiden substituutio on tietyssä määrin mahdollista.
lineaarisen isokantin tapauksessa substituutiojousto olisi ääretön ja L: n muotoisten isokanttien tapauksessa nolla.
ISO-Kustannuskäyrä
Iso-kustannuskäyrä on kaikkien erilaisten työn ja pääoman yhdistelmien pisteiden lokus, joita organisaatio voi käyttää näiden panosten hinnan perusteella. Iso-cost-linja kuvaa tekijöiden hintaa yhdessä sen rahamäärän kanssa, jonka organisaatio on valmis käyttämään tekijöihin.
toisin sanoen siinä näkyy erilaisia tekijöiden yhdistelmiä, joita voi ostaa tietyllä rahamäärällä. Iso-kustannuslinjan kaltevuus riippuu työn hinnan ja pääoman hinnan suhteesta.
esimerkiksi tuottajan kokonaisbudjetti on ₹120, jonka hän haluaa käyttää tuotannontekijöihin eli X: ään ja Y: hen.X: n hinta markkinoilla on ₹15 yksikköä kohti ja Y: n hinta on ₹10 yksikköä kohti. Taulukossa 7.5 esitetään yhdistelmät:
| yhdistelmät | X: n yksiköt | Y: n yksiköt | menot yhteensä |
|---|---|---|---|
| A | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
iso-kustannuslinja on esitetty kuvassa 7.8:
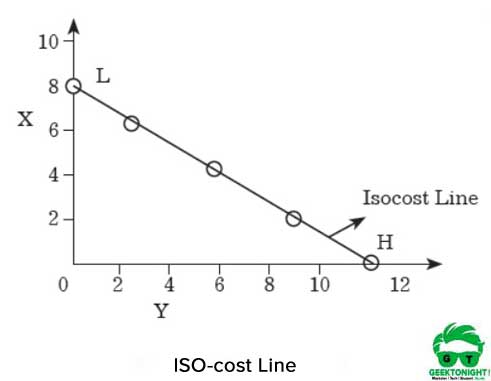
kuten kuviosta 6 ilmenee, jos tuottaja käyttää koko rahamäärän X: n ostamiseen, hän voi ostaa 8 X: n yksikköä.toisaalta, jos tuottaja ostaa Y: n koko summalla, hän voi saada 12 yksikköä.
jos pisteet H ja L yhtyvät vastaavasti X-ja Y-akseleilla, saadaan suora, jota kutsutaan iso-kustannusjonoksi. Kaikki yhdistelmät X ja Y, jotka sijaitsevat tällä rivillä, olisi sama määrä kustannuksia, joka on ₹120.
samoin muut iso-kustannuslinjat voidaan piirtää ottamalla kustannukset yli 120, jos tuottaja on valmis käyttämään enemmän rahaa tuotannontekijöihin.
isoquant-ja iso-cost-linjojen avulla tuottaja voi määrittää, missä vaiheessa tuotantopanokset tuottavat maksimivoiton minimikustannusten avulla. Tällaista kohtaa kutsutaan tuottajan tasapainoksi.
Lue Myös: Cardinal and Ordinal Utility
Business Economics Tutorial
(klikkaa aihetta lukeaksesi)
Go On, Share article with Friends
Leave a Reply