31 Formules mathématiques d’ACTE Que vous devez connaître

Géométrie plane

Angles et lignes

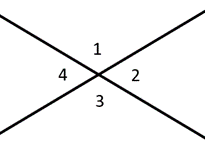
Les angles le long d’une ligne sont appelés angles supplémentaires, additionnant jusqu’à \(180^{\circ}\). Les angles complémentaires s’additionnent à \(90^{\circ}\), un angle droit. Les angles verticaux décrivent des angles directement en face les uns des autres, qui sont toujours congruents. Dans le diagramme de gauche, par exemple, nous dirions que les angles 1 & 2 sont supplémentaires, tandis que les angles 1 & 3 sont des angles verticaux.

Aire d’un triangle

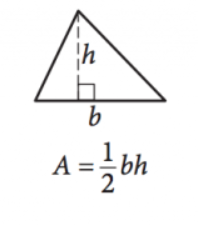
Image reproduite avec l’aimable autorisation de SAT

\(\frac{1}{2} bh=A\)

Cette équation fournit l’aire \((A)\) de tout triangle donné des longueurs de la base \((b)\) et de la hauteur \((h)\). Notez que la hauteur est la longueur de la ligne s’étendant selon un angle complémentaire de n’importe quel côté (la base) jusqu’au point / angle directement en face de ce côté.

Pour les triangles équilatéraux, où les trois côtés \((s)\) ont la même longueur, l’équation d’aire est:

\(\frac{s^2\sqrt{3}}{4} = A\)

Théorème de Pythagore

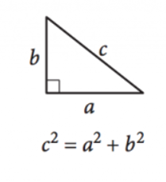
Image reproduite avec l’aimable autorisation de SAT

Comme les angles d’un triangle s’additionnent toujours à \(180^{\circ}\), un triangle rectangle est défini comme n’importe quel triangle avec un angle droit, ce qui garantit que les deux autres angles sont complémentaires. Les longueurs latérales des triangles rectangles peuvent être définies par le théorème de Pythagore:

\(a^2 + b^2 = c^2\)

Ici, \(a\) et \(b\) sont les longueurs des jambes, ou les côtés en face des angles complémentaires, et \(c\) est la longueur de l’hypoténuse, le côté en face de l’angle droit.

Il peut être utile de mémoriser également les triplets pythagoriciens suivants, ou les valeurs pour les longueurs de côté \((a, b, c)\): 3-4-5, 5-12-13, 7-24-25, et 8-15-17. Notez que l’hypoténuse est toujours le côté le plus long.

Triangles rectangles spéciaux

Il existe deux types de triangles rectangles spéciaux, qui ont les rapports d’angles et de longueur comme suit:

Image reproduite avec l’aimable autorisation de SAT

Aires de quadrilatères

\(A=lw\)

Cette formule fournit l’aire d’un rectangle de longueur \(l\) et de largeur \(w\).

\(A= bh\)

Cette formule fournit l’aire d’un parallélogramme donné en base \(b\), la longueur des côtés les plus longs et la hauteur \(h\), définie comme la longueur de la ligne s’étendant selon un angle complémentaire d’une base à l’autre.

\(A= \frac {b_1+b_2} {2} \:\ fois\:h\)

Cette formule fournit l’aire d’un trapèze avec les bases \(b_1\) et \(b_2\) et la hauteur \(h\), définies de la même manière que pour les parallélogrammes.

Angles intérieurs de polygones réguliers

\((n-2)\:\times\: 180^{\circ}= S\)

Dans un polygone régulier, où tous les côtés et angles sont égaux, cette formule fournit la somme \((S)\) des angles intérieurs étant donné un polygone avec \(n\) côtés et angles. Nous pouvons également trouver chaque angle intérieur en calculant \(\frac{S}{n}\).

Longueur d’arc dans un cercle

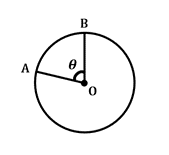
\(\ frac {\thêta}{360^{\circ}}\:\ fois\:2\pi r = arc\:length\)

Cette formule définit la longueur de l’arc, ou section de la circonférence du cercle, entre deux rayons donnés se coupant au centre du cercle avec un angle central \(\thêta\). Notez que le \(2\pi r\) intègre la circonférence du cercle dans cette formule.

Zone de secteur dans un cercle

\(\frac{\theta}{360^{\circ}} \:\times\: \ pi r ^2 = secteur\: zone\)

Semblable à la longueur de l’arc, cette formule fournit l’aire du secteur entre deux rayons donnés se croisant au centre du cercle avec un angle central. Le \(\pi r ^2\) incorpore l’aire du cercle dans cette formule.

Formes 3D

\(SA = 2(lw + wh + lh)\)

\( V = lwh\)

Ces formules fournissent la surface \((SA)\) et le volume \((V)\) pour un prisme rectangulaire de longueur \(l\), largeur \(w\) et hauteur \(h\).

\(V = \pi r ^2h\)

C’est la formule de volume pour un cylindre droit avec un rayon de base \(r\) et une hauteur \(h\).

Si vous avez besoin des formules de surface ou de volume pour toute autre forme 3D, l’ACT fournira des formules pertinentes dans les questions elles-mêmes.

Trigonométrie

SOH-CAH-TOA

La plupart des problèmes de trigonométrie ACT impliquent la manipulation du sinus, du cosinus et de la tangente, qui sont calculés comme suit pour un angle donné \(x\) dans un triangle rectangle:

\(sin(x) = \frac{opposite\:leg}{hypoténuse}\)

\( cos(x) = \frac {adjacent\:leg} {hypoténuse}\)

\( tan(x) = \frac {opposé\:jambe} { adjacent\: jambe} = \frac {sin(x)} {cos(x)}\)

SOH-CAH-TOA est un mnémonique facile pour se souvenir de quelle fonction trigonométrique correspond à quelles longueurs de côté!

Identités de fonctions

\(sin(x) = cos(90^{\circ}-x)\)

\( cos(x) = sin(90^{\circ}-x)\)

En mots, ces identités montrent qu’une fonction trigonométrique d’angle \(x\) est égale à la valeur de la cofonction du complément de \(x\). Ils sont généralement utilisés lorsqu’il s’agit de trigonométrie plus avancée, permettant des conversions faciles entre sinus et cosinus.

Identités de Rapport / Trigonométrie réciproque

Vous pouvez parfois voir les identités réciproques de \(sin(x)\), \(cos(x)\) et \(tan(x)\), qui sont:

\(csc(x) = \frac {1} {sin(x)}\)

\( sec(x) = \frac {1} {cos(x)}\)

\( cot(x) = \frac {1} {tan(x)}\)

Identité pythagoricienne

\(sin^2(x) + cos^2(x)=1\)

Sur la base du théorème de Pythagore et du cercle unitaire, cette identité est généralement utilisée aux côtés des identités de cofonctions pour résoudre des problèmes de trigonométrie (sans calculatrice) où l’angle \(x\) ou les valeurs de ces fonctions trigonométriques de \(x\) sont inconnues.

Statistiques et probabilités

Pourcentages

\(n\%\: of\:m = \frac{n}{100}\:\ fois\:m\)

Les pourcentages sont utilisés pour exprimer des parties d’un tout, et le symbole \(\%\) signifie généralement “diviser par 100.”En tant que telle, l’équation ci-dessus répond à tout problème demandant \(n\%\) de la quantité \(m\).

Moyenne, Médiane, Mode et Plage

La LOI teste les connaissances statistiques de base, impliquant généralement les mesures ci-dessous:

• La moyenne est la moyenne, ou \(\frac { sum\: of\:all\:terms} { total\:number\:of\:termes }\)
• La médiane est le terme moyen, ou la moyenne des deux termes moyens s’il existe un nombre pair de termes
• Le mode est le terme (s) qui se produit le plus fréquemment
• La plage est la différence entre les termes les plus grands et les plus petits

Probabilité

\(P(A) = \frac { nombre\ : of\:desired\:outcomes} {total\:number\: of\:possible\:outcomes}\)

La probabilité représente la probabilité qu’un événement\((A)\) se produise, calculée en divisant le nombre de résultats souhaités par le nombre total de résultats possibles. Par exemple, la probabilité de lancer un 6 sur un dé pair est \(\frac{1}{6}\).

Événements indépendants

\(P(A\: et \:B) = P(A)\:\ times\: P(B)\)

Les événements \(A\) et \(B\) sont indépendants si \(A\) survenant n’affecte pas la probabilité que \(B\) survienne. Pour calculer la probabilité que les deux événements indépendants se produisent, nous multiplions leurs probabilités individuelles ensemble. Par exemple, la probabilité de retourner la tête deux fois est \(\frac{1}{2}\:\times\:\frac{1}{2} = \frac{1}{4}\).

Enveloppant

Nous avons couvert beaucoup de formules dans cet article, mais assurez-vous également de revoir tous les concepts mathématiques à travers l’Algèbre II et la géométrie! Par exemple, vous pouvez vous attendre à ce que des nombres complexes, des vecteurs, des matrices, des systèmes d’équations et des fonctions graphiques manipulatrices soient également testés. Voir cette description complète de la section ACT math pour plus d’informations.

Rappelez-vous que la pratique rend parfait, surtout pour les mathématiques! Vous voudrez essayer beaucoup de problèmes différents avant le jour du test, dans le but de vraiment comprendre comment appliquer et intégrer ces concepts et formules en temps opportun.

Comme vous avez le droit d’avoir une calculatrice pour l’ACTE, nous vous conseillons d’en apporter une, mais avec un mot de prudence. N’oubliez pas que chaque problème mathématique d’ACTE peut être résolu sans calculatrice, et il est facile de perdre un temps précieux en utilisant votre calculatrice alors que vous n’en avez pas besoin. En tant que tel, faites des sections d’entraînement chronométrées avec votre calculatrice si vous prévoyez d’en apporter une, et rappelez-vous qu’elle n’est là qu’en dernier recours: pour faciliter les calculs et augmenter votre vitesse. Atteignez-le rarement et vérifiez que votre modèle spécifique est autorisé conformément à la politique ACT calculator.