Courbe Isoquante: Définition, Propriétés, Types, Hypothèses
Qu’est-ce que la courbe isoquante?
Courbe isoquante: Une relation technique qui montre comment les entrées sont converties en sorties est représentée par une courbe isoquante. Il montre les combinaisons optimales d’intrants factoriels à l’aide des prix des intrants factoriels et de leurs quantités utilisées pour produire la même production.
Le terme ISO implique égal et quant signifie quantité ou sortie.
Par exemple, pour produire 100 calendriers, 90 unités de capital et 10 unités de travail sont utilisées.
Les courbes isoquantes sont également appelées courbes de produit égal ou courbes d’indifférence de production.
Définition de la courbe isoquante
Hypothèses de la courbe isoquante
Les hypothèses d’une courbe isoquante sont les suivantes:
- Il n’y a que deux facteurs de production, le travail et le capital, pour produire un produit particulier.
- Le capital, le travail et les biens sont divisibles par nature.
- Le capital et le travail peuvent se substituer jusqu’à une certaine limite.
- La technologie de production est donnée sur une période de temps.
- Les facteurs de production sont utilisés avec une efficacité totale.
Apprenons l’isoquant à l’aide du tableau suivant.
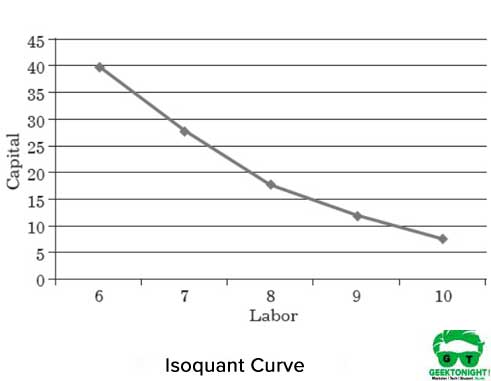
Le tableau 1 montre les différentes combinaisons de deux facteurs de production, à savoir le travail et le capital pour produire 150 tonnes de production:
| Travail | Capital |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
La figure 1 montre la courbe isoquante de différentes combinaisons de capital-travail qui aident à produire 150 tonnes de production:
Propriétés de la courbe isoquante
Certaines des propriétés de la courbe isoquante sont les suivantes:
- Les courbes isoquantes s’inclinent vers le bas
- Les courbes isoquantes sont convexes à l’origine
- Les courbes isoquantes ne peuvent pas se croiser
- Plus l’isoquante est élevée, plus la sortie est élevée

Les courbes isoquantes s’inclinent vers le bas
Cela implique que la pente de la courbe isoquante est négative. En effet, lorsque le capital (K) est augmenté, la quantité de travail (L) est réduite ou vice versa, pour maintenir le même niveau de production.
Les courbes isoquantes sont convexes à l’origine
Cela implique que les entrées de facteurs ne sont pas des substituts parfaits. Cette propriété montre la substitution des intrants et le taux marginal décroissant de substitution technique de l’isoquant. La signification marginale d’un intrant (capital) par rapport à un autre intrant (travail) diminue avec la courbe isoquante.
La figure 2 montre la courbe isoquante convexe:
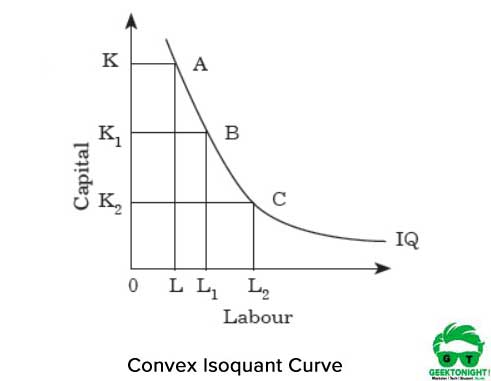
La convexité représente que le MRTS diminue si l’on se déplace du point A à B et de B à C le long de l’isoquant. Les TMT diminuent parce que les deux intrants travail et capital ne sont pas des substituts parfaits.
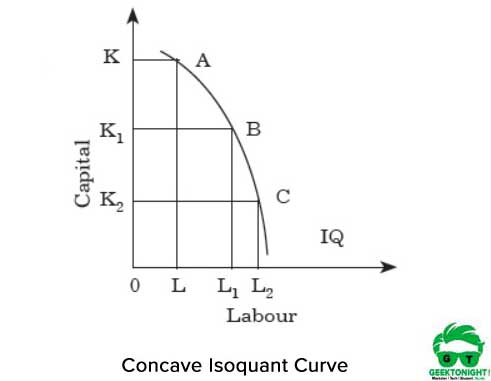
Ainsi, pour chaque augmentation du travail, il y a une diminution du capital. Si isoquant est concave, les MRT du travail pour le capital augmentent. La figure 3 montre la courbe isoquante concave:
Comme le montre la figure 3, si nous passons du point A à B et de B à C le long de l’isoquant, le MRTS augmente. Il montre que les deux intrants travail et capital sont de parfaits substituts. Ainsi, pour chaque augmentation du travail, il y a une augmentation du capital.
Les courbes isoquantes ne peuvent pas se croiser
Une isoquante implique les différents niveaux de combinaison produisant différents niveaux d’entrées. Si les isoquantes se croisent, cela impliquerait qu’une seule combinaison d’entrée peut produire deux niveaux de sortie, ce qui n’est pas possible. Le droit de la production ne serait pas applicable.
Plus l’isoquant est élevé, plus la sortie
est élevée, cela implique que l’isoquant supérieur représente une sortie plus élevée. La courbe supérieure de l’isoquant produit plus de sortie que la courbe inférieure. En effet, la plus grande combinaison d’entrées se traduit par une sortie plus grande par rapport à la courbe qui se trouve en dessous.
Taux marginal de Substitution Technique
La pente de la courbe isoquante est le taux de substitution qui montre comment une entrée peut être substituée à une autre tout en maintenant la sortie constante. C’est ce qu’on appelle le taux marginal de substitution technique (TMT).
Selon Lipsey, “le taux marginal de substitution technique peut être défini comme le taux auquel un facteur est remplacé par un autre avec une production maintenue constante.”
La formule de calcul des MRT est la suivante:
MRTS = -KK /LL
où,KK = Variation du capital
LL = Variation du travail
La formule montre qu’à un niveau de production donné, MRTS du capital pour le travail impliquerait la quantité de travail que l’entreprise serait prête à abandonner pour une unité de capital supplémentaire. De même, les MRT de la main-d’œuvre pour le capital impliqueraient la quantité de capital que l’entreprise serait prête à abandonner pour une unité de main-d’œuvre supplémentaire.
Le MRTS est également égal au rapport entre le produit marginal d’un intrant et le produit marginal d’un autre intrant. La sortie le long de l’isoquant est constante. Si la variation du travail remplace la variation du capital, alors l’augmentation de la production due à l’augmentation du travail devrait correspondre à la diminution de la production due à la diminution du capital. Mathématiquement
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Depuis la sortie reste inchangé, à un isoquant,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
Ainsi, on peut dire que les TRM entre les entrées est égale à produits marginaux des entrées.
Le MRTS est calculé comme indiqué dans le tableau 2
| Travail | Capital | TMT |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
Types de courbe isoquante
Il y a une substitution continue d’une variable d’entrée par l’autre variable d’entrée à un rythme décroissant. Des compléments parfaits et des substituts parfaits donnent différentes formes d’isoquants.
Les différents types de courbe isoquante sont les suivants:
- Isoquant linéaire
- isoquant en forme de L

Isoquant linéaire
C’est un isoquant en ligne droite et représente une substituabilité parfaite entre les intrants, le capital et le travail de la fonction de production. Les MRT entre les entrées restent constantes. La figure 4 montre un isoquant linéaire:
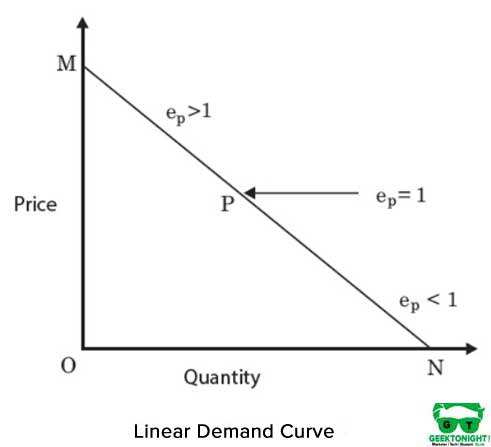
La forme algébrique de la fonction de production en cas d’isoquant linéaire est la suivante:
Q = aK + BL
Ici, Q est la somme pondérée de K et L. La pente de la courbe peut être calculée à l’aide de la formule suivante:
MPK =QQ /KK = a
MPL =QQ /LL = b
MRTS = MPL/MPK
MRTS = -b /a (b /a est constant)
Cependant, l’isoquant linéaire n’a pas d’existence dans le monde réel.
Isoquant en forme de L
C’est le cas des compléments parfaits. Dans ce cadre, la combinaison entre le capital et le travail est dans une proportion fixe. Une seule combinaison de travail et de capital est possible pour produire un produit avec une proportion d’intrants fixée.
Pour augmenter la production, une organisation doit augmenter proportionnellement les deux intrants. La représentation graphique de l’isoquant à proportion de facteur fixe est de forme L, représentée sur la figure 5:
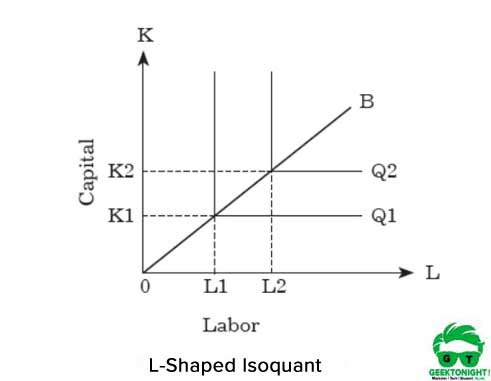
Comme le montre la figure 5, l’isoquant en forme de L représente qu’il n’y a pas de substitution entre le travail et le capital et qu’ils sont supposés être des biens complémentaires. On peut voir que les unités de capital OK1 et les unités de travail OL1 sont nécessaires pour la production de Q1.
D’autre part, pour augmenter la production de Q1 à Q2, une organisation doit augmenter les intrants de K1 à K2 et de L1 à L2 à la fois. Cette relation entre le capital et le travail peut s’exprimer comme suit:
Q = f(K, L) = min(aK, bL)
où, min implique Q est égal au plus bas des deux termes, aK et bL
Par exemple, dans le cas AK > bL, alors Q = bL et dans le cas AK < BL alors, Q = aK.
Cet isoquant est identique à la fonction de production de leontif.
Élasticité de Substitution Entre les Facteurs
On sait que MRTS est la pente de l’isoquant. Cependant, il ne révèle pas le degré de substituabilité d’un facteur à un autre. Il est important de mesurer le degré de substituabilité entre les deux entrées.
Par conséquent, les économistes ont développé une formule pour estimer l’étendue de la substituabilité entre les deux intrants, le capital et le travail, connue sous le nom d’élasticité de la substitution factorielle.
L’élasticité de la substitution factorielle (σ) fait référence au rapport entre la variation en pourcentage du rapport capital-travail et la variation en pourcentage des TMT.
Il est représenté mathématiquement comme suit:
σ = variation en pourcentage du ratio capital-travail / variation en pourcentage des TEM
Ou,
σ = *
SiKK /LL =MRMRTS ; σ = 1
Si ∆K/∆L > ∆TRM ; σ > 1
Si ∆K/∆L < ∆TRM ; σ < 1
Haute élasticité de substitution entre les facteurs implique que les facteurs peuvent facilement être substitués les uns aux autres, tandis qu’une faible élasticité représente que la substitution de facteurs est possible dans une certaine mesure.
Dans le cas d’une isoquante linéaire, l’élasticité de substitution serait infinie, et dans le cas d’isoquantes en forme de L, elle serait nulle.
Courbes de coûts ISO
La courbe de coûts Iso est le lieu des points de toutes les différentes combinaisons de travail et de capital qu’une organisation peut employer, compte tenu du prix de ces intrants. La ligne Iso-coût représente le prix des facteurs ainsi que le montant d’argent qu’une organisation est prête à dépenser pour les facteurs.
En d’autres termes, il montre différentes combinaisons de facteurs qui peuvent être achetés avec une certaine somme d’argent. La pente de la ligne iso-coût dépend du rapport entre le prix du travail et le prix du capital.
Par exemple, un producteur a un budget total de 120 ₹, qu’il souhaite dépenser pour les facteurs de production, à savoir X et Y. Le prix de X sur le marché est de 15 per l’unité et le prix de Y est de 10 per l’unité. Le tableau 7.5 présente les combinaisons:
| Combinaisons | Unités de X | Unités de Y | Dépenses totales |
|---|---|---|---|
| A | 8 | 0 | 120 |
| D | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
La ligne iso-coût est illustrée à la figure 7.8:
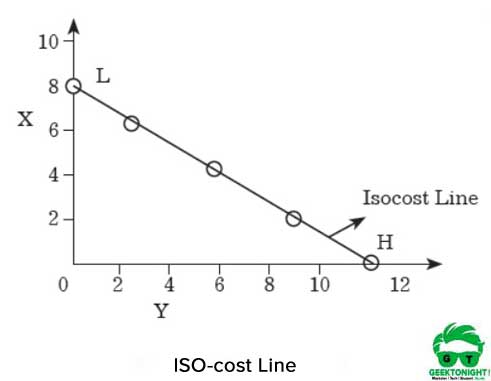
Comme le montre la figure 6, si le producteur dépense la totalité de l’argent pour acheter X, il peut acheter 8 unités de X. Par contre, si le producteur achète Y avec la totalité du montant, il pourra obtenir 12 unités.
Si les points H et L sont joints sur les axes X et Y, respectivement, une droite est obtenue, appelée ligne iso-cost. Toutes les combinaisons de X et Y qui se trouvent sur cette ligne auraient le même coût qui est de 120 ₹.
De même, d’autres lignes de coûts iso peuvent être tracées en prenant un coût supérieur à 120, au cas où le producteur serait prêt à dépenser plus d’argent pour les facteurs de production.
À l’aide des lignes isoquant et iso-cost, un producteur peut déterminer le point auquel les intrants génèrent un profit maximal en engageant un coût minimal. Un tel point est appelé équilibre du producteur.
Lire aussi: Utilitaire Cardinal et Ordinal
Tutoriel d’économie d’entreprise
(Cliquez sur le sujet pour lire)
Continuez, Partagez l’article avec des amis
Leave a Reply