31 ACT matematikai képletek, amelyeket tudnia kell

sík geometria

szögek és vonalak

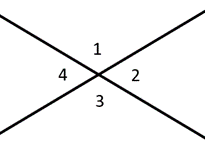
a vonal mentén lévő szögeket kiegészítő szögeknek nevezzük, amelyek összege \(180^{\circ}\). A kiegészítő szögek összege \(90^{\circ}\), derékszög. A függőleges szögek közvetlenül egymással szemben lévő szögeket írnak le, amelyek mindig egybevágóak. A bal oldali ábrán például azt mondanánk, hogy az 1 & 2 szögek kiegészítőek, míg az 1 & 3 szögek függőleges szögek.

háromszög területe

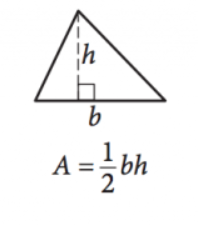
Kép jóvoltából sat

\(\frac{1}{2}bh=a\)

ez az egyenlet megadja a terület \((a)\) bármely háromszög adott hosszúságú bázis \((b)\) és magasság \((h)\). Vegye figyelembe, hogy a magasság annak a vonalnak a hossza, amely komplementer szögben nyúlik ki bármely oldalról (az alapról) egészen a pontig/szögig, közvetlenül az adott oldalról.

egyenlő oldalú háromszögek esetén, ahol mind a három oldal \((s)\) azonos hosszúságú, a területegyenlet:

\(\frac{s^2 \ sqrt{3}}{4}=A\)

Pitagorasz-tétel

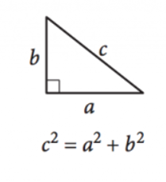
Kép jóvoltából sat

mivel a háromszög szögei mindig \(180^{\circ}\) értéket adnak, a derékszögű háromszög bármely háromszög, amelynek egy derékszöge van, biztosítva, hogy a másik két szög egymást kiegészítse. A derékszögű háromszögek oldalhosszait a Pitagorasz-tétel határozhatja meg:

\(a^2 + b^2=c^2\)

itt \(a\) és \(b\) a lábak hossza, vagy a komplementer szögekkel szemben lévő oldalak, és \(c\) a hipotenusz hossza, a derékszöggel szemben lévő oldal.

hasznos lehet megjegyezni a következő Pitagorasz-hármasokat vagy az oldalhossz értékeit \((a, b,c)\): 3-4-5, 5-12-13, 7-24-25, és 8-15-17. Ne feledje, hogy a hypotenuse mindig a leghosszabb oldal.

speciális derékszögű háromszögek

kétféle speciális derékszögű háromszög létezik, amelyek szöge és hosszaránya a következő:

Kép jóvoltából SAT

négyszögek területei

\(A = lw\)

ez a képlet egy téglalap területét adja meg, amelynek hossza \(l\) és szélessége \(w\).

\(A = bh\)

ez a képlet adja meg a paralelogramma területét , a \(b\) bázist, a leghosszabb oldalak hosszát és a \(h\) magasságot, amely az egyik bázistól a másikig terjedő kiegészítő szögben húzódó vonal hossza.

\(a=\frac{b_1+b_2}{2}\:\alkalommal\:h\)

ez a képlet adja meg a trapéz területét \(b_1\) és \(b_2\) alapokkal és \(h\) magassággal, ugyanúgy definiálva, mint a paralelogrammák esetében.

Szabályos sokszögek belső szögei

\((n-2)\:\times\:180^{\circ}= S\)

egy szabályos sokszögben, ahol minden oldal és szög egyenlő, ez a képlet adja meg az \(N\) oldalú és szögű sokszög belső szögeinek összegét. Az egyes belső szögeket a \(\frac{S}{n}\) kiszámításával is megtalálhatjuk.

ívhossz egy körben

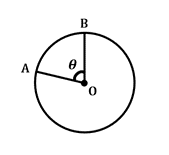
\(\frac {\theta} {360^{\circ}}\: \ alkalommal\:2 \ pi r = ív\: hossz\)

ez a képlet határozza meg az ív vagy a kör kerületének hosszát két adott sugár között, amelyek a kör közepén keresztezik a középső szöget \(\theta\). Vegye figyelembe, hogy a \(2\pi r\) magában foglalja a kör kerületét ebbe a képletbe.

szektor területe egy körben

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = szektor\:terület\)

az ívhosszhoz hasonlóan ez a képlet megadja a szektor területét két adott sugár között, amelyek a kör közepén keresztezik egymást központi szöggel . A\ (\pi r^2\) magában foglalja a kör területét ebbe a képletbe.

3D formák

\(SA = 2 (lw + wh + lh)\)

\(V= lwh\)

ezek a képletek megadják a \((SA)\) felületet és a \((V)\) térfogatot egy téglalap alakú prizmához, amelynek hossza \(l\), szélessége \(w\) és magassága \(h\).

\(V=\pi r^2h\)

ez egy jobb oldali henger térfogatképlete, amelynek alapsugara \(r\) és magassága \(h\).

ha bármilyen más 3D-s alakzathoz szüksége van a felület vagy a térfogat képletekre, az ACT magában a kérdésben releváns képleteket biztosít.

trigonometria

SOH-CAH-TOA

a legtöbb ACT trig probléma magában foglalja a szinusz, koszinusz és érintő manipulálását, amelyeket a következőképpen kell kiszámítani egy derékszögű háromszög adott szögére:

\(sin (x)= \ frac{szemben\: leg}{hypotenuse}\)

\(cos (x)= \ frac{szomszédos\: láb}{hipotenusz}\)

\(tan (x)= \ frac{szemben\: láb}{szomszédos\: láb}= \ frac{sin (x)} {cos (x)}\)

a SOH-CAH-TOA egy egyszerű emlékeztető, amely megjegyzi, hogy melyik trig funkció melyik oldalhossznak felel meg!

Cofunction Identities

\(sin (x) = cos (90^{\circ} – x)\)

\(cos(x) = sin(90^{\circ}-x)\)

szavakban ezek az identitások azt mutatják, hogy az \(x\) szög trig-függvénye megegyezik a \(x\) komplementjének társfunkciójának értékével. Ezeket általában a fejlettebb trigonometria kezelésére használják, lehetővé téve a szinusz és a koszinusz közötti könnyű konverziót.

Arány / reciprok Trig identitások

alkalmanként láthatja a \(sin(x)\), \(cos(x)\) és \(tan(x)\) kölcsönös identitásait, amelyek:

\(csc (x) = \ frac{1}{sin (x)}\)

\(sec (x) =\frac{1}{cos (x)}\)

\(kiságy (x) = \ frac{1}{tan (x)}\)

Pitagoraszi identitás

\(sin^2(x)+cos^2 (x)=1\)

a Pitagorasz-tétel és az egységkör alapján ezt az identitást általában a cofunction identitások mellett használják a trig-problémák megoldására(sans kalkulátor), ahol az \(x\) szög vagy ezeknek az \(x\) trig-függvényeknek az értékei ismeretlenek.

statisztika és valószínűség

százalék

\(n\%\: of\: m = \ frac{n}{100}\: \ times\:m\)

a százalékokat az egész részeinek kifejezésére használják, és a \(\%\) szimbólum általában azt jelenti, hogy “oszd meg 100-zal.”Mint ilyen, a fenti egyenlet válaszol minden olyan problémára, amely \(n\%\) mennyiséget kér \(m\).

átlag, medián, mód és tartomány

az ACT teszteli az alapvető statisztikai ismereteket, általában az alábbi intézkedések bevonásával:

• az átlag az átlag, vagy \(\frac{sum\: of\: all\: terms}{total\: number\: of\:feltételek}\)
• Medián a középső kifejezés, vagy a két középső kifejezés átlaga, ha páros számú kifejezés van
• mód a leggyakrabban előforduló kifejezés(ek)
• tartomány a legnagyobb és a legkisebb kifejezés közötti különbség

valószínűség

\(P(A) = \frac{szám\:of\:kívánt\:eredmények}{total\:number\:of\:lehetséges\:eredmények}\)

a valószínűség egy \((a)\) esemény bekövetkezésének valószínűségét jelenti, amelyet úgy kell kiszámítani, hogy a kívánt eredmények számát elosztjuk az összes lehetséges kimenetel számával. Például annak a valószínűsége, hogy egy 6-ot egy egyenletes kockára dobunk, \(\frac{1}{6}\).

független események

\(P(A\:and\:B) = P(A)\:\times\:P(B)\)

az \(A\) és \(B\) események függetlenek, ha \(a\) bekövetkezése nem befolyásolja a \(B\) bekövetkezésének valószínűségét. Annak a valószínűségnek a kiszámításához, hogy mindkét független esemény bekövetkezik,megszorozzuk az egyes valószínűségeket. Például a fejek kétszeri megfordításának valószínűsége \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

csomagolás fel

már lefedett sok képletek ebben a bejegyzésben, de biztos, hogy is vizsgálja felül az összes matematikai fogalmak révén Algebra II és geometria! Például elvárható, hogy komplex számok, vektorok, mátrixok, egyenletrendszerek és grafikus függvények manipulálása is szerepeljen a tesztben. További információkért lásd az ACT math szakasz teljes leírását.

ne feledje, hogy a gyakorlat teszi a mestert, különösen a matematika! Sok különböző problémát szeretne kipróbálni a tesztnap előtt, azzal a céllal, hogy valóban megértse, hogyan kell ezeket a fogalmakat és képleteket időben alkalmazni és integrálni.

mivel megengedett egy számológép a törvényhez, javasoljuk, hogy hozzon egyet, de óvatosan. Ne feledje, hogy minden ACT matematikai probléma megoldható számológép nélkül, és könnyű értékes időt pazarolni a számológép használatával, amikor valójában nem kell. Mint ilyen, nem időzített gyakorlat szakaszok a számológép, ha azt tervezi, hogy egy, ne feledje, hogy ez csak ott, mint a legvégső: a számítások megkönnyítése és a sebesség növelése érdekében. Ritkán érje el, és ellenőrizze, hogy az adott modell megengedett-e az ACT kalkulátor házirendje szerint.