31 Formule matematiche ACT che devi sapere

Geometria piana

Angoli e linee

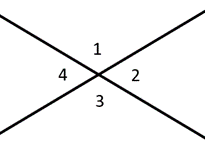
Gli angoli lungo una linea sono chiamati angoli supplementari, aggiungendo fino a \(180^{\circ}\). Gli angoli complementari si sommano a \(90^{\circ}\), un angolo retto. Gli angoli verticali descrivono gli angoli direttamente uno di fronte all’altro, che sono sempre congruenti. Nel diagramma a sinistra, ad esempio, diremmo che gli angoli 1 & 2 sono supplementari, mentre gli angoli 1 & 3 sono angoli verticali.

Area di un triangolo

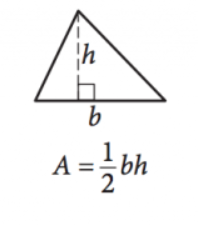
Immagine gentilmente concessa da SAT

\(\frac{1}{2}bh=A\)

Questa equazione fornisce l’area \((A)\) di qualsiasi triangolo dato lunghezze della base \((b)\) e altezza \((h)\). Si noti che l’altezza è la lunghezza della linea che si estende ad un angolo complementare da qualsiasi lato (la base) fino al punto/angolo direttamente di fronte a quel lato.

Per i triangoli equilateri, dove tutti e tre i lati \((s)\) hanno la stessa lunghezza, l’equazione dell’area è:

\(\frac{s^2\sqrt{3}}{4}=A\)

Teorema di Pitagora

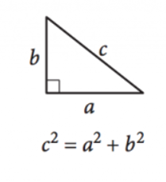
Immagine per gentile concessione di SAT

Come gli angoli in un triangolo sempre aggiungere fino a \(180^{\circ}\), di un triangolo rettangolo è definito come qualsiasi triangolo con un angolo retto, assicurando gli altri due angoli sono complementari. Le lunghezze laterali dei triangoli rettangoli possono essere definite dal Teorema di Pitagora:

\(a^2 + b^2=c^2\)

Qui, \(a\) e \(b\) sono le lunghezze delle gambe, o i lati di fronte agli angoli complementari, e \(c\) è la lunghezza dell’ipotenusa, il lato di fronte all’angolo retto.

Può essere utile memorizzare anche le seguenti triple pitagoriche o valori per le lunghezze laterali \((a, b, c)\): 3-4-5, 5-12-13, 7-24-25, e 8-15-17. Si noti che l’ipotenusa è sempre il lato più lungo.

Triangoli rettangoli speciali

Esistono due tipi di triangoli rettangoli speciali, che hanno gli angoli e i rapporti di lunghezza come segue:

Immagine gentilmente concessa da SAT

Aree di quadrilateri

\(A = lw\)

Questa formula fornisce l’area di un rettangolo con lunghezza \(l\) e larghezza \(w\).

\(A = bh\)

Questa formula fornisce l’area di un parallelogramma dato base \(b\) , la lunghezza dei lati più lunghi e l’altezza \(h\), definita come la lunghezza della linea che si estende ad un angolo complementare da una base all’altra.

\(A= \ frac{b_1+b_2}{2}\: \ volte\:h\)

Questa formula fornisce l’area di un trapezio con basi \(b_1\) e \(b_2\) e altezza \(h\), definita allo stesso modo dei parallelogrammi.

Angoli interni di poligoni regolari

\((n-2)\:\times\:180^{\circ}= S\)

In un poligono regolare, dove tutti i lati e gli angoli sono uguali, questa formula fornisce la somma \((S)\) degli angoli interni dato un poligono con \(n\) lati e angoli. Possiamo anche trovare ogni angolo interno calcolando \(\frac{S} {n}\).

Lunghezza dell’arco in un cerchio

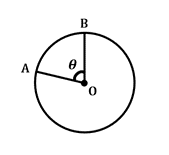
\(\frac {\theta}{360^{\circ}}\: \ volte\:2 \ pi r = arc\: length\)

Questa formula definisce la lunghezza dell’arco, o sezione della circonferenza del cerchio, tra due raggi dati che si intersecano al centro del cerchio con l’angolo centrale \(\theta\). Si noti che il \(2\pi r\) incorpora la circonferenza del cerchio in questa formula.

Area di settore in un cerchio

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = settore\:area\)

Simile alla lunghezza dell’arco, questa formula fornisce l’area del settore tra due raggi dati che si intersecano al centro del cerchio con l’angolo centrale . Il \ (\pi r^2\) incorpora l’area del cerchio in questa formula.

Forme 3D

\(SA = 2 (lw + wh + lh)\)

\(V= lwh\)

Queste formule forniscono l’area di superficie \((SA)\) e volume \((V)\) per un prisma rettangolare con lunghezza \(l\), larghezza \(w\) e altezza \(h\).

\(V=\pi r^2h\)

Questa è la formula del volume per un cilindro destro con raggio di base \(r\) e altezza \(h\).

Se hai bisogno delle formule di superficie o volume per qualsiasi altra forma 3D, l’ATTO fornirà formule pertinenti nelle domande stesse.

Trigonometria

SOH-CAH-TOA

Più ATTO trig problemi che coinvolgono la manipolazione di seno, coseno e tangente, che sono calcolati come segue per un dato angolo \(x\) in un triangolo rettangolo:

\(sin(x)=\frac{opposto\:gamba}{ipotenusa}\)

\(cos(x)=\frac{adiacenti\:gamba}{ipotenusa}\)

\(tan(x)=\frac{opposto\:gamba}{adiacenti\:gamba}=\frac{sin(x)}{cos(x)}\)

SOH-CAH-TOA è un facile mnemonico per ricordare che trig funzione corrisponde a lunghezze!

Cofunction Identità

\(sin(x) = cos(90^{\circ}-x)\)

\(cos(x) = sin(90^{\circ}-x)\)

In parole, queste identità mostrare che un trig funzione dell’angolo \(x\) è uguale al valore del cofunction del complemento di \(x\). Sono generalmente utilizzati quando si tratta di trigonometria più avanzata, consentendo conversioni facili tra seno e coseno.

Rapporto/Identità trigonometriche reciproche

Occasionalmente è possibile vedere le identità reciproche di\ (sin (x)\), \(cos (x)\) e \(tan (x)\), che sono:

\(csc(x) =\frac{1}{sin(x)}\)

\(sec(x) =\frac{1}{cos(x)}\)

\(cot(x) =\frac{1}{tan(x)}\)

Pitagora Identità

\(sin^2(x)+cos^2(x)=1\)

Basato sul Teorema di Pitagora e il cerchio unitario, questa identità è generalmente utilizzato in aggiunta alla cofunction identità per risolvere trig problemi (senza calcolatrice) dove l’angolo \(x\) o i valori delle funzioni trigonometriche di \(x\) sono sconosciuti.

Statistica e Probabilità

Percentuali

\(n\%\: di\: m = \ frac{n}{100}\:\volte\:m\)

Le percentuali vengono utilizzate per esprimere parti di un intero e il simbolo \ ( \ % \ ) generalmente significa “dividi per 100.”Come tale, l’equazione di cui sopra risponde a qualsiasi problema che richiede \(n\%\) di quantità \(m\).

Media, Mediana, Modalità e intervallo

L’atto verifica le conoscenze statistiche di base, generalmente coinvolgendo le misure seguenti:

• Media è la media, o \(\frac {sum\: of\: all\: terms} {total\:number\: of\:termini}\)
• Mediana è il termine medio, o la media delle due metà se vi è un numero pari di termini
• Modalità è il termine(s) che si verifica più frequentemente
• serie è la differenza tra il più grande e il più piccolo dei termini

Probabilità

\(P(A) = \frac{numero\:di\:desiderato\:risultati}{totale\:numero\:di\:possibile\:i risultati}\)

Probabilità rappresenta la probabilità di un evento \((A)\) che si verificano, calcolato dividendo il numero di risultati auspicati per il numero totale di possibili risultati. Ad esempio, la probabilità di tirare un 6 su un dado pari è \(\frac{1}{6}\).

Eventi Indipendenti

\(P(A\:e\B) = P(A)\:\times\:P(B)\)

Eventi \(A\) e \(B\) sono indipendenti se \(A\) che si verificano non influisce sulla probabilità di \(B\) che si verificano. Per calcolare la probabilità che si verifichino entrambi gli eventi indipendenti, moltiplichiamo insieme le loro probabilità individuali. Ad esempio, la probabilità di capovolgere le teste due volte è \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

Avvolgendolo

Abbiamo coperto un sacco di formule in questo post, ma essere sicuri di rivedere anche tutti i concetti matematici attraverso Algebra II e Geometria! Per esempio, ci si può aspettare numeri complessi, vettori, matrici, sistemi di equazioni, e la manipolazione di funzioni grafiche per essere sul test pure. Vedi questa descrizione completa della sezione ACT math per maggiori informazioni.

Ricorda che la pratica rende perfetti, soprattutto per la matematica! Ti consigliamo di provare molti problemi diversi prima del giorno del test, con l’obiettivo di capire davvero come applicare e integrare questi concetti e formule in modo tempestivo.

Come si è permesso un calcolatore per l’atto, vi consigliamo di portare uno, ma con una parola di cautela. Ricordate che ogni problema di matematica atto può essere risolto senza una calcolatrice, ed è facile perdere tempo prezioso utilizzando la calcolatrice quando in realtà non è necessario. Come tale, fare sezioni di pratica a tempo con la calcolatrice se si prevede di portare uno, e ricordate che è solo lì come ultima risorsa: per facilitare i calcoli e aumentare la velocità. Raggiungilo raramente e controlla che il tuo modello specifico sia consentito dalla politica della calcolatrice ACT.