Curva isoquante: Definizione, Proprietà, Tipi, Ipotesi
Che cosa è la curva Isoquant?
Curva isoquante: una relazione tecnica che mostra come gli input vengono convertiti in output è rappresentata da una curva isoquante. Mostra le combinazioni ottimali di input di fattori con l’aiuto dei prezzi degli input di fattori e delle loro quantità utilizzate per produrre lo stesso output.
Il termine ISO implica uguale e quant significa quantità o output.
Ad esempio, per la produzione di 100 calendari, vengono utilizzate 90 unità di capitale e 10 unità di lavoro.
Le curve isoquanti sono anche chiamate curve di prodotto uguali o curve di indifferenza di produzione.
Definizione della curva isoquante
Ipotesi di curva isoquante
Le ipotesi di una curva isoquante sono le seguenti:
- Ci sono solo due fattori di input, lavoro e capitale, per produrre un particolare prodotto.
- Capitale, lavoro e beni sono di natura divisibile.
- Capitale e lavoro sono in grado di sostituirsi a vicenda fino a un certo limite.
- La tecnologia di produzione è data per un periodo di tempo.
- I fattori di produzione sono utilizzati con piena efficienza.
Impariamo isoquant con l’aiuto della seguente tabella.
Tabella 1 mostra le diverse combinazioni dei due fattori, vale a dire, di capitale e di lavoro per la produzione di 150 tonnellate di output:
| Lavoro | Capitale |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
Figura 1 mostra la curva di isoquanto di lavoro diverse capitali combinazioni che aiutano nella produzione di 150 tonnellate di output:
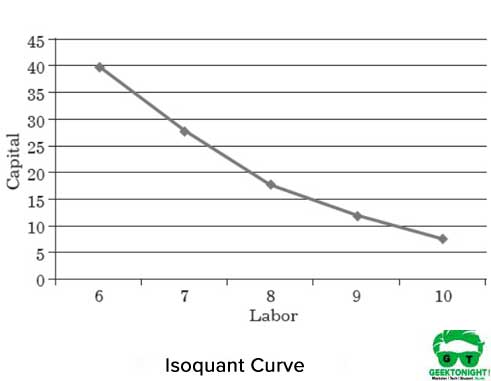
le Proprietà della Curva di Isoquanto
Alcune delle proprietà di curva di isoquanto sono come segue:
- Isoquanto curve in pendenza verso il basso
- Isoquanto curve convesse di origine
- Isoquanto curve non si intersecano
- Maggiore l’isoquanto più il segnale di output

Isoquanto curve in pendenza verso il basso
implica che la pendenza della curva di isoquanto è negativo. Questo perché quando il capitale (K) viene aumentato, la quantità di lavoro (L) viene ridotta o viceversa, per mantenere lo stesso livello di produzione.
Le curve isoquanti sono convesse all’origine
Implica che gli input del fattore non sono sostituti perfetti. Questa proprietà mostra la sostituzione degli input e la diminuzione del tasso marginale di sostituzione tecnica di isoquant. Il significato marginale di un input (capitale) in termini di un altro input (lavoro) diminuisce insieme alla curva isoquante.
La figura 2 mostra la curva isoquante convessa:
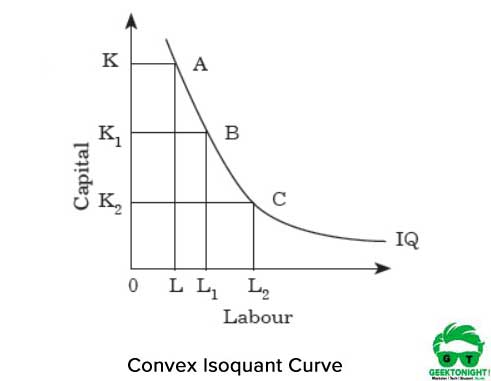
La convessità rappresenta che l’MRTS diminuisce se ci spostiamo dal punto A a B e da B a C lungo l’isoquante. Gli MRT diminuiscono perché i due fattori produttivi lavoro e capitale non sono sostituti perfetti.
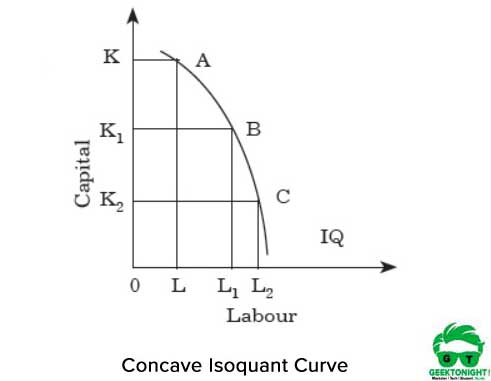
Quindi, per ogni aumento del lavoro, c’è una diminuzione del capitale. Se isoquant è concavo, i MRT di lavoro per aumenti di capitale. La figura 3 mostra la curva isoquante concava:
Come mostrato nella Figura 3, se passiamo dal punto A a B e da B a C lungo l’isoquante, l’MRTS aumenta. Essa dimostra che i due input lavoro e capitale sono perfetti sostituti. Quindi, per ogni aumento del lavoro, c’è un aumento del capitale.
Le curve isoquanti non possono intersecarsi tra loro
Un isoquante implica i diversi livelli di combinazione che producono diversi livelli di input. Se gli isoquanti si intersecano, ciò implicherebbe che una singola combinazione di input può produrre due livelli di output, il che non è possibile. La legge di produzione non sarebbe applicabile.
Più alto è l’isoquante più alto è l’output
Implica che l’isoquante più alto rappresenta un output più alto. La curva superiore dell’isoquante produce più output della curva sottostante. Questo perché la combinazione più ampia di input produce un output più grande rispetto alla curva sottostante.
Tasso marginale di sostituzione tecnica
La pendenza della curva isoquante è il tasso di sostituzione che mostra come un input può essere sostituito con un altro mantenendo costante l’output. Questo è chiamato tasso marginale di sostituzione tecnica (MRTS).
Secondo Lipsey, ” il tasso marginale di sostituzione tecnica può essere definito come il tasso al quale un fattore viene sostituito da un altro con un output mantenuto costante.”
La formula per calcolare MRT è la seguente:
MRT = – ∆K/∆L
dove, ∆K = Variazione del capitale
∆L= Variazione in termini di lavoro
La formula mostra che, ad un dato livello di output, MRT di capitale per lavoro, comporterebbe la quantità di lavoro che l’azienda sarebbe disposta a rinunciare per un’unità aggiuntiva di capitale. Analogamente, gli MRT di lavoro per capitale implicherebbero l’importo di capitale che l’impresa sarebbe disposta a rinunciare per un’unità di lavoro aggiuntiva.
MRTS è anche uguale al rapporto tra prodotto marginale di un input e prodotto marginale di un altro input. L’uscita lungo l’isoquante è costante. Se la variazione del lavoro è sostituita dalla variazione del capitale, allora l’aumento della produzione dovuto all’aumento del lavoro dovrebbe corrispondere alla diminuzione della produzione dovuta alla diminuzione del capitale. Matematicamente
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Dato che l’uscita rimane invariato a un dato isoquanto,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
Quindi, possiamo dire che MRT tra ingressi è pari a marginale di prodotti di ingressi.
La MRT è calcolata come indicato in Tabella 2
| Lavoro | Capitale | MRT |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
Tipi di curva isoquante
Esiste una sostituzione continua di una variabile di ingresso con l’altra variabile di ingresso a una velocità decrescente. Complementi perfetti e sostituti perfetti danno diverse forme di isoquanti.
I diversi tipi di curva isoquante sono i seguenti:
- Lineare isoquanto
- a forma di L isoquanto

Lineare isoquanto
è una linea retta isoquanto e rappresenta una perfetta sostituibilità tra gli ingressi, il capitale e il lavoro della funzione di produzione. MRT tra gli ingressi rimane costante. La figura 4 mostra un isoquante lineare:
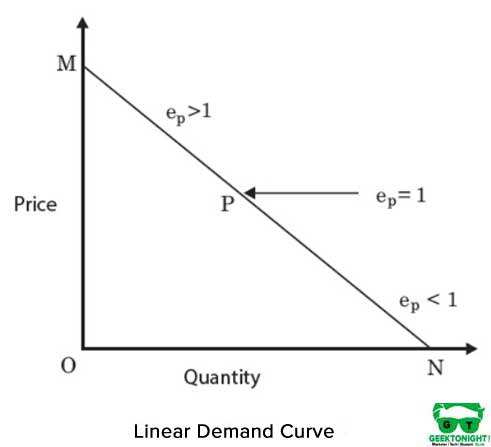
La forma algebrica della funzione di produzione in caso di lineare isoquanto è come indicato di seguito:
Q = aK + BL
Qui, Q è la somma ponderata di K e L. La pendenza della curva può essere calcolato con l’aiuto della seguente formula:
MPK = ∆Q/∆K = a
MPL = ∆Q/∆L = b
MRT = MPL / MPK
MRT = -b/a b/a è costante)
Tuttavia, lineare isoquanto non hanno esistenza nel mondo reale.
Isoquant a forma di L
Questo è il caso dei complementi perfetti. In base a ciò, la combinazione tra capitale e lavoro è in una proporzione fissa. Solo una combinazione di lavoro e capitale è possibile produrre un prodotto con percentuale apposta di input.
Per aumentare la produzione, un’organizzazione deve aumentare proporzionalmente entrambi gli input. La rappresentazione grafica del fattore fisso proporzione isoquant è L in forma, mostrato in Figura 5:
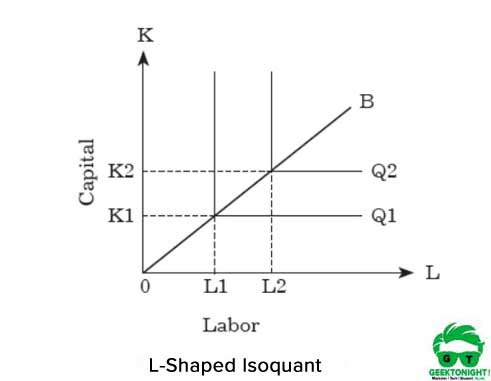
Come mostrato nella figura 5, l’isoquante a forma di L rappresenta che non vi è alcuna sostituzione tra lavoro e capitale e si presume che siano beni complementari. Si può vedere che le unità di capitale OK1 e le unità di lavoro OL1 sono necessarie per la produzione di Q1.
D’altra parte, per aumentare la produzione da Q1 a Q2, un’organizzazione deve aumentare gli input da K1 a K2 e da L1 a L2 entrambi. Questa relazione tra capitale e lavoro può essere espressa come segue:
Q = f (K, L) = min (aK, bL)
dove, min implica Q uguale a inferiore dei due termini, aK e bL
Ad esempio, nel caso aK > bL, quindi Q = bL e nel caso aK < bL quindi, Q = aK.
Questo isoquant è lo stesso della funzione di produzione leontif.
Elasticità di sostituzione tra fattori
Sappiamo che MRTS è la pendenza dell’isoquante. Tuttavia, non rivela il grado di sostituibilità di un fattore all’altro. È importante misurare il grado di sostituibilità tra i due input.
Pertanto, gli economisti hanno sviluppato una formula per stimare l’entità della sostituibilità tra i due input, capitale e lavoro, che è nota come elasticità della sostituzione dei fattori.
L’elasticità della sostituzione dei fattori (σ) si riferisce al rapporto tra la variazione percentuale del rapporto capitale-lavoro e la variazione percentuale degli MRT.
È rappresentato matematicamente come segue:
σ = variazione percentuale del rapporto capitale lavoro / variazione percentuale degli MRT
Oppure,
σ = *
Se K K / L L = MR MRT ; σ = 1
Se ∆K/∆L > ∆MRT ; σ > 1
Se ∆K/∆L < ∆MRT ; σ < 1
Elevata elasticità di sostituzione tra fattori implica che i fattori possono essere facilmente sostituito, mentre una bassa elasticità rappresenta che la sostituzione di fattori è possibile in una certa misura.
In caso di isoquante lineare, l’elasticità di sostituzione sarebbe infinita, e in caso di isoquanti a forma di L, sarebbe zero.
Curve di costo ISO
La curva di costo iso è il luogo di punti di tutte le diverse combinazioni di lavoro e capitale che un’organizzazione può impiegare, dato il prezzo di questi input. La linea Iso-cost rappresenta il prezzo dei fattori insieme alla quantità di denaro che un’organizzazione è disposta a spendere per i fattori.
In altre parole, mostra diverse combinazioni di fattori che possono essere acquistati con una certa somma di denaro. La pendenza della linea iso-cost dipende dal rapporto tra il prezzo del lavoro e il prezzo del capitale.
Ad esempio, un produttore ha un budget totale di ₹120, che vuole spendere per i fattori di produzione, vale a dire X e Y. Il prezzo di X sul mercato è di ₹15 per unità e il prezzo di Y è di unit 10 per unità. La tabella 7.5 illustra le combinazioni:
| Combinazioni | Unità di X | Unità di Y | spesa Totale |
|---|---|---|---|
| Un | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
iso-costo linea è mostrato in Figura 7.8:
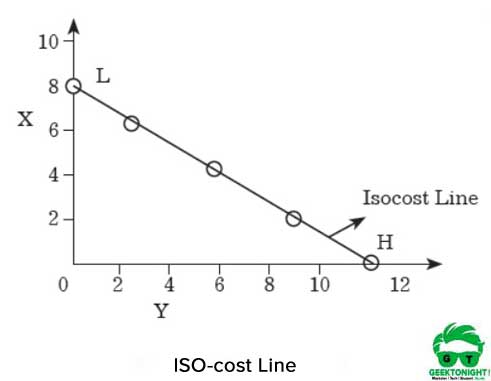
Come mostrato in Figura 6, se il produttore spende l’intero ammontare di denaro per l’acquisto di X, allora si può acquistare 8 unità di X. d’altra parte, se il produttore acquisti Y con l’intero importo, poi lui/lei sarebbe in grado di ottenere un campione di 12 unità.
Se i punti H e L sono uniti rispettivamente sugli assi X e Y, si ottiene una linea retta, che viene chiamata linea iso-cost. Tutte le combinazioni di X e Y che si trovano su questa linea, avrebbero la stessa quantità di costo che è ₹120.
Allo stesso modo, altre linee iso-costo possono essere tracciati prendendo costo più di 120, nel caso in cui il produttore è disposto a spendere più quantità di denaro sui fattori di produzione.
Con l’aiuto di linee isoquant e iso-cost, un produttore può determinare il punto in cui gli input producono il massimo profitto incorrendo in costi minimi. Tale punto è definito come l’equilibrio del produttore.
Leggi anche: Il cardinale e Ordinale Utilità
Economia Aziendale Tutorial
(Clicca sull’Argomento a Leggere)
Andare Su, Condividi l’articolo con gli Amici
Leave a Reply