折り紙花びら折りとは|Abrashi Origami School

花弁の折り目は、適度に複雑な折り目のグループに属します。 それは単一の線に沿って折り目として記述することができないのでそうです。

それにもかかわらず、それは絶対的な初心者によって定期的に実行されます。 花びらの折り目は、古典的な鳥の基部の折り畳み時の折り目の1つとしてよく使用されます（図1）。 したがって、あなたが絶対的な初心者であっても、あなたはすでに1つを折ることが良いチャンスがあります。

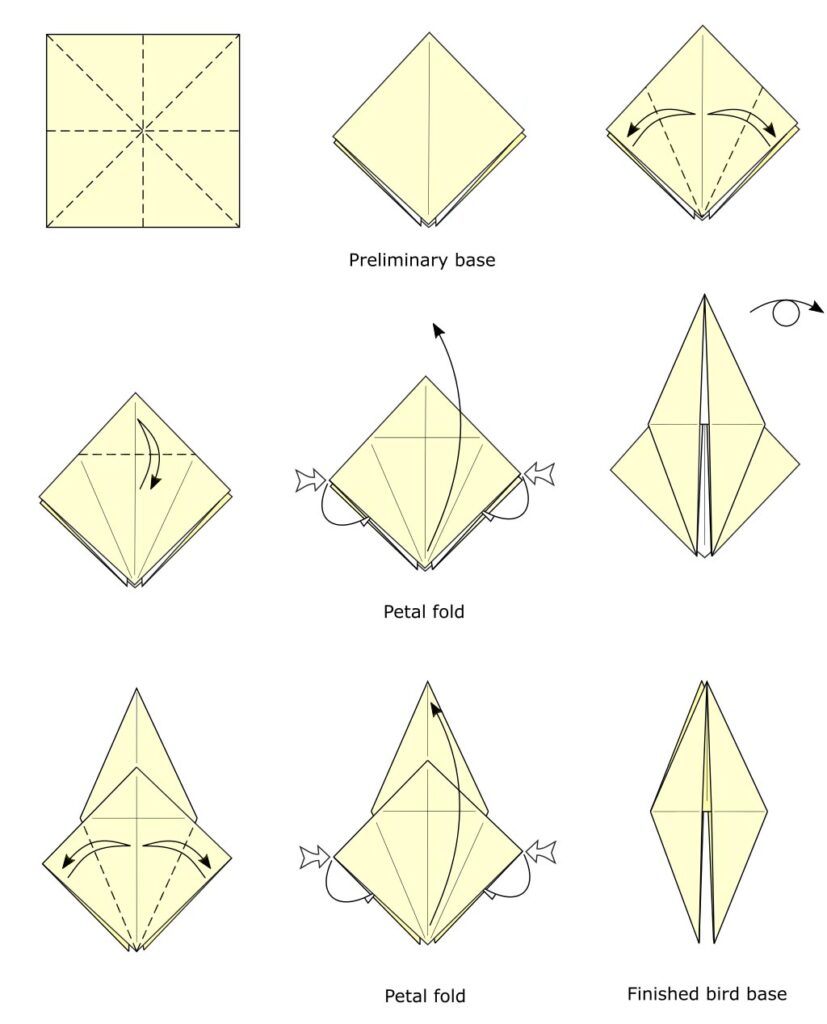
花びらの折り畳み-単純な実装

しかし、なぜ私は花びらの折り畳みが鳥のベースの折り畳みの間に”最も頻繁に”使用されると言ったのですか。 花びらの折り畳みの実装に頼らずに鳥のベースを折り畳むことは可能ですか？ まあ、不思議なことに、鳥のベースの場合、答えはイエスです。 図2に示す手順を分析すると、花弁の折り目が全くないことに気付くでしょう。 その代わりに、内部には2つの逆折畳（A）と1つの単純折畳（B）があります。 それにもかかわらず、最終的な結果は同じです。

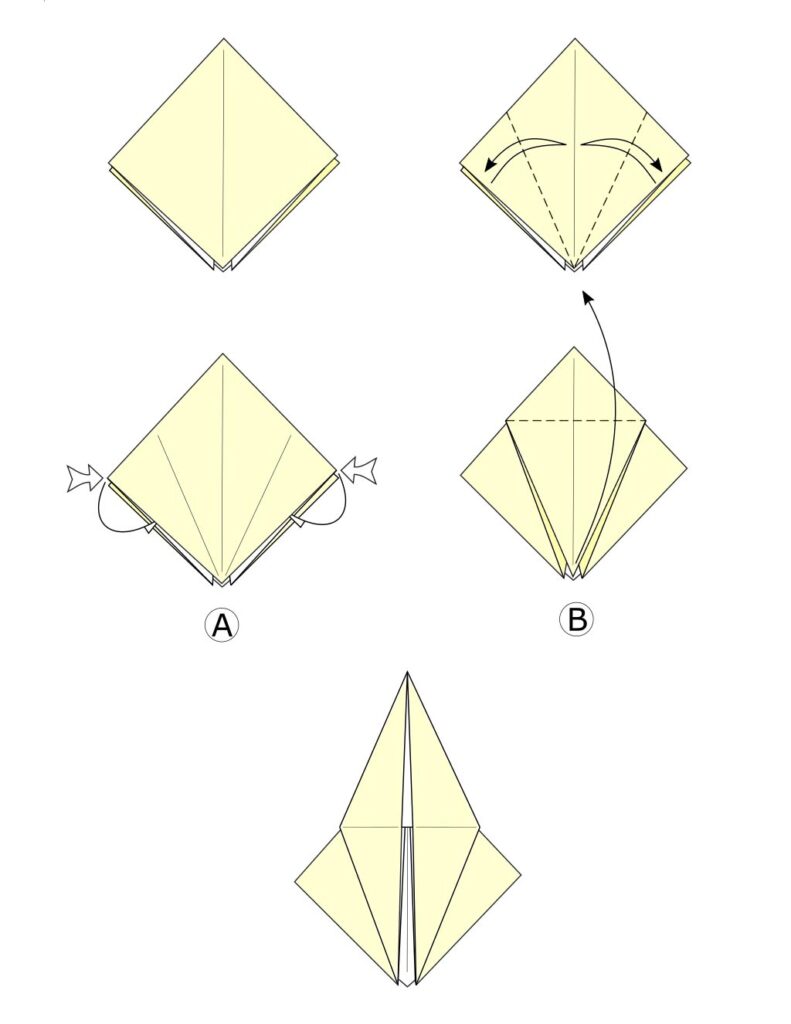
この新しい手順を元の手順と比較すると、最初の手順で複数の折り目を同時に折り畳むことが求められていることがすぐにわかります。 一方、第二のアプローチは、単純な折り目のシーケンスのより多くのです。

だから、やっぱり花びらの折りとは何ですか？ それはいくつかの単純な折り目のシーケンスですか、それとも彼自身の権利で折り目ですか？

その質問に答える前に、別の簡単な例をお見せしましょう（図3を見てください）。

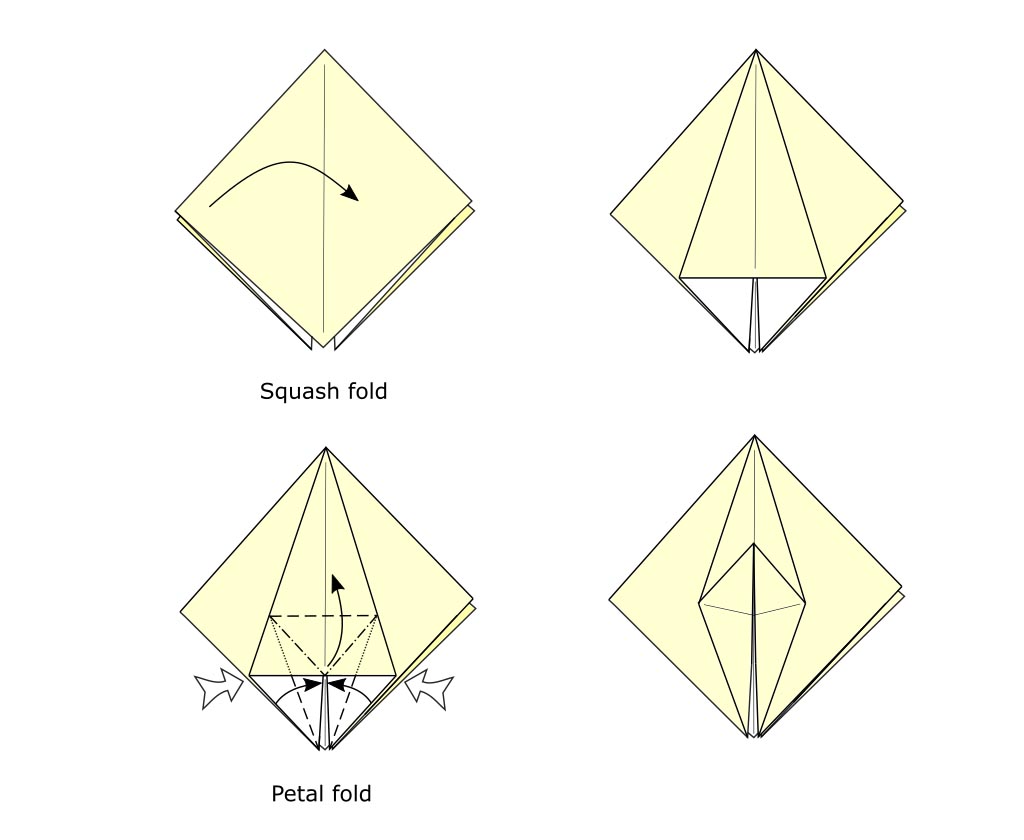
再び我々は花びらの折り畳みを行った（図3）。 しかし、図2に示すように、同じアプローチを実装しようとすると、花びらの折り方が予想よりも少し複雑であることがすぐにわかります。 言い換えれば、図2に示す単純化されたアプローチは、ここでは機能しないか、少なくともそれほどエレガントには機能しません。 これは私たちに何を言っていますか？ まあ、それは単純な折り目のシーケンスに花びらの折り目を打破するエレガントな方法がない場合、花びらの折り目は確かにそれ自身の権利で倍でなけ ほとんどすべての必要な折り目を事前に折り目を付けることさえできます（図3を見てください）が、それでも段階的に折り畳むことはできません。

さらに悪いことに、花びらの折り目のより複雑なアプリケーションでは、事前の折り目なしで花びらの折り目を実行することを余儀なくされます。 言い換えれば、あなたは折り紙の初心者のために非常に困難である、その場で花びらの折りを実行する必要があります。 それが花弁の折り目が適度に複雑であると考えられる唯一の理由です。

花びらのひだとウサギの耳

以前に示された花びらのひだの例を分析すると、花びらのひだの珍しい特徴があるかもしれません。 彼らは、実際には、2つの対称的に配置されたウサギの耳で構成されています。 図4を見てください。

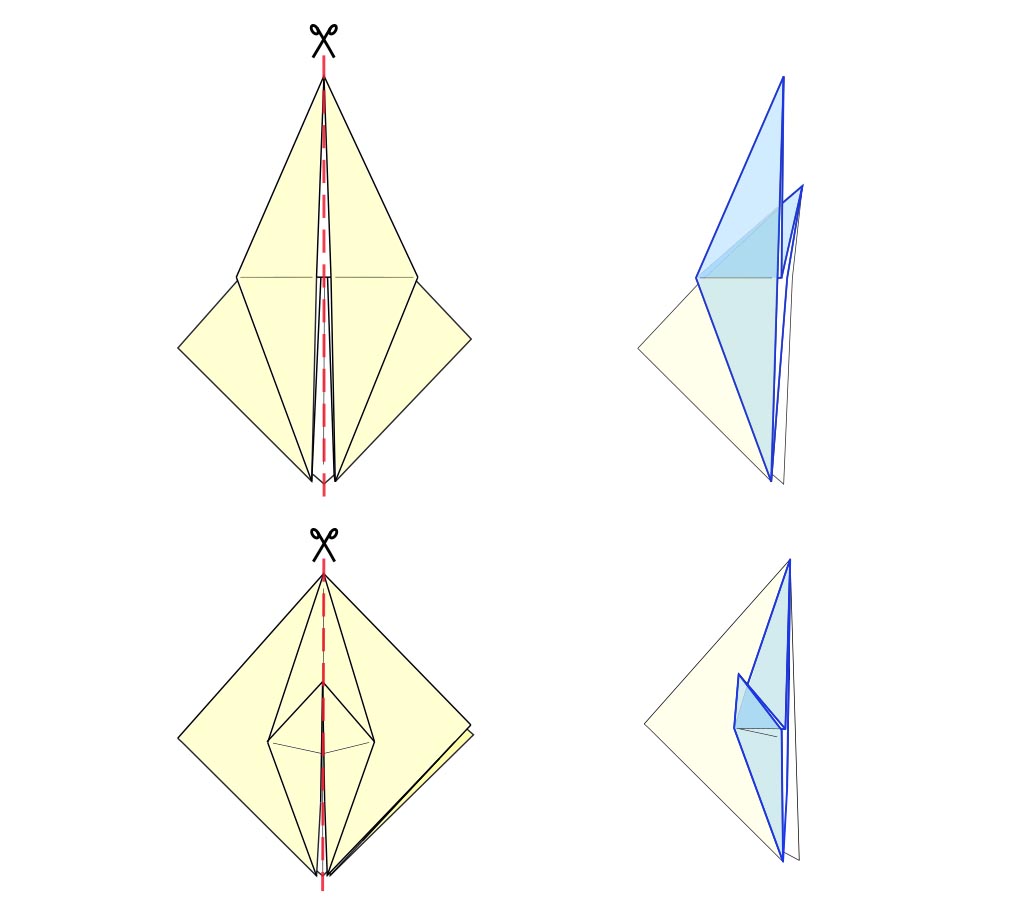
だから、これは花びらの折り目の定義ですか？ 花びらの折り目は、対称的に配置されたウサギの耳以上のものではありません。 たぶん、そうではないかもしれません。 しかし、正直に言うと、これは私が同意できる定義です。 結局のところ、花びらの折り目の最も引用された例は、鳥のベースのものです。 そして、鳥のベースを分析すると（伝統的な折り紙ベースのブログ記事を見て）、鳥のベースはウサギの耳の数だけで構成されていることがわかります。

だから、定義は論理的なようですか？ しかし、残念なことに、花弁の折り目のより複雑な実装を見つけることができます。 たとえば、加藤周樹の本;Nature Study,36ページ（ステップ7-10）では、そのようなより複雑な例を見つけることができます（図5）。

ちょうど示された花びらの折り目も2つの対称的に配置されたウサギの耳で構成されていると主張することは可能ですか？ 私はそうは思わない。 しかし、著者の加藤周樹でさえ、これが本物の花びらの折り目であることを確信していなかったので、彼はそれを花びらのような折り目と呼んだ。 だから、私は前の単純な定義に固執することをお勧めします。