等量曲線：定義、プロパティ、タイプ、仮定

等量曲線とは何ですか？

等量曲線:入力が出力にどのように変換されるかを示す技術的な関係は、等量曲線によって描かれています。 これは、因子入力の価格と同じ出力を生成するために使用されるそれらの数量の助けを借りて、因子入力の最適な組み合わせを示しています。

isoという用語は等しいことを意味し、quantは量または出力を意味します。

たとえば、100のカレンダーを作成するには、90単位の資本と10単位の労働が使用されます。

等量曲線は、等積曲線または生産無関心曲線とも呼ばれます。

等量曲線の定義

等量曲線の仮定

等量曲線の仮定は次のとおりです:

• 特定の製品を生産するためには、労働と資本の2つの要素投入しかありません。
• 資本、労働、財は本質的に割り切れる。
• 資本と労働は、一定の限度まで相互に代替することができます。
• 生産の技術は一定期間にわたって与えられます。
• 生産要素は完全な効率で使用されます。

次の表の助けを借りて、isoquantを学びましょう。

表1は、150トンの出力を生産するための労働と資本の二つの要因入力の異なる組み合わせを示しています:

労働	資本金
6	40
7	28
8	18
9	12
10	8

図1は、150トンの出力を生成するのに役立つ異なる労働資本の組み合わせの等量曲線を示しています:

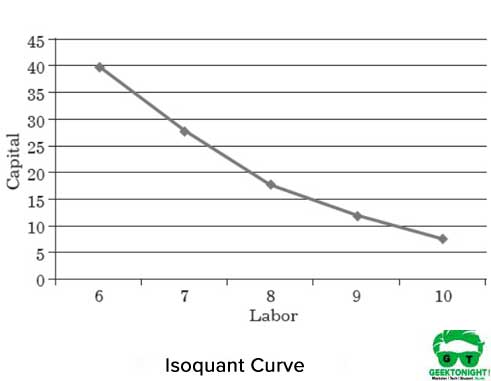
等量曲線の性質

等量曲線の性質のいくつかは次のとおりです:

1. 等量曲線は下向きに傾きます
2. 等量曲線は原点に凸です
3. 等量曲線は互いに交差できません
4. 等量が高いほど出力が高くなります

等量曲線は下方向に傾きます

等量曲線の傾きが負であることを意味します。 これは、資本（K）が増加すると、労働量（L）が減少するか、またはその逆であり、同じレベルの出力を維持するためである。

等量曲線は原点に凸である

これは、因子入力が完全な代替ではないことを意味します。 この特性は，入力の置換と等量の技術的置換の限界率の減少を示す。 ある入力（資本）の別の入力（労働）の観点からの限界的意義は、等量曲線とともに減少する。

図2は、凸の等量曲線を示しています:

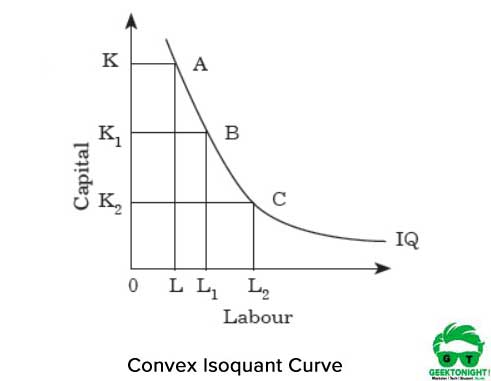
凸性は、点Aからbへ、およびbからcへ等量に沿って移動すると、MRTが減少することを表します。 MRTは、労働と資本の2つの入力が完全な代替品ではないため、減少します。

したがって、労働の増加ごとに、資本の減少がある。 Isoquantが凹面であれば、資本のための労働のMRTSが増加します。

図3に示すように、a点からb点、b点からc点へ等分線に沿って移動すると、MRTが増加します。 これは、労働と資本の2つの入力が完全な代替品であることを示しています。 したがって、労働のすべての増加のために、資本の増加があります。

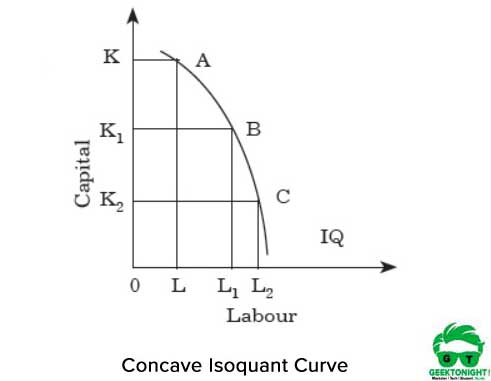
等量曲線は互いに交差することはできません

等量曲線は、異なるレベルの組み合わせを意味し、異なるレベルの入力を生成します。 等量が互いに交差する場合、単一の入力の組み合わせが2つのレベルの出力を生成できることを意味しますが、これは不可能です。 生産の法則は適用されないでしょう。

アイソクアントが高いほど出力が高くなります

アイソクアントが高いほど出力が高くなることを意味します。 等量の上の曲線は、下の曲線よりも多くの出力を生成します。 これは、入力の組み合わせが大きいほど、その下にある曲線と比較して出力が大きくなるためです。

技術的置換の限界率

等量曲線の傾きは、出力を一定に保ちながら、ある入力を別の入力にどのように置き換えることができるかを示す置換率で これは限界技術代替率（MRT）と呼ばれています。

Lipseyによると、「技術的代替の限界率は、出力が一定に保たれている一方の因子が別の因子に置換される率として定義することができる。”

MRTSを計算するための式は次のとおりです:
MRTS=–≤K/≤L
ここで、≤K=資本の変化
≤L=労働の変化

この式は、与えられた出力レベルで、労働のための資本のMRTSは、会社が追加の資本単位のために放棄しても構わないと思う労働の量を意味することを示している。 同様に、資本のための労働のMRTは、会社が労働の追加単位のためにあきらめて喜んでであろう資本の量を意味するであろう。

MRTSはまた、ある入力の周辺積と別の入力の周辺積の比にも等しい。 等量に沿った出力は一定です。 労働の変化が資本の変化に置き換えられる場合、労働の増加による生産量の増加は、資本の減少による生産量の減少と一致するはずである。 数学的に

∆L x MPL=∆K x MPk
∆Q=∆L x MPL+∆K x MPk

の出力に変更はないたisoquant,

∆L x MPL+∆K x MPk=0

(MPL/MPK)=(-∆K/∆L)

MRTSKL=(MPL/MPK)

こうということMRTS間入力が限界的な製品を用の入力端子が付いています。

MRTSは表に示すように計算されます2

労働	資本	MRTS
6	40
7	28	12:1
8	18	10:1
9	12	6:1
10	8	4:1

等量曲線の種類

減少率で一方の入力変数を他方の入力変数に連続的に代入することがあります。 完全な補足物および完全な代理はisoquantsの異なった形態を与える。

等量曲線の種類は次のとおりです:

1. 線形アイソクアント
2. L字型アイソクアント

Linear isoquant

これは直線isoquantであり、生産関数の入力、資本、労働の間の完全な置換性を表します。 入力間のMRTSは一定のままです。 図4は、線形等量を示しています:

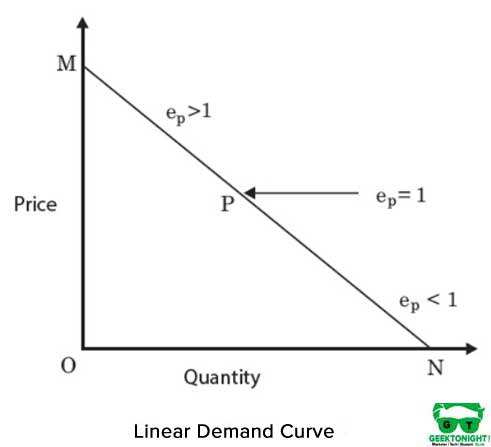
線形等量の場合の生産関数の代数形式は次のとおりです：

Q=aK+BL

ここで、QはKとLの加重和です。:

MPK=√Q/√K=a
MPL=√Q/√L=b
MRTS=MPL/MPK
MRTS=-b/a(b/aは定数)

しかし、線形等量は現実世界には存在しません。

L字型アイソクアン

これは完璧な補完の場合です。 この下では、資本と労働の組み合わせは一定の割合にあります。 労働と資本の一つの組み合わせだけが入力の固定割合を持つ製品を生産することが可能です。

生産を増やすためには、組織は両方の投入量を比例的に増やす必要があります。 固定因子比率等量のグラフ表現は、図に示すように、形状がLです5:

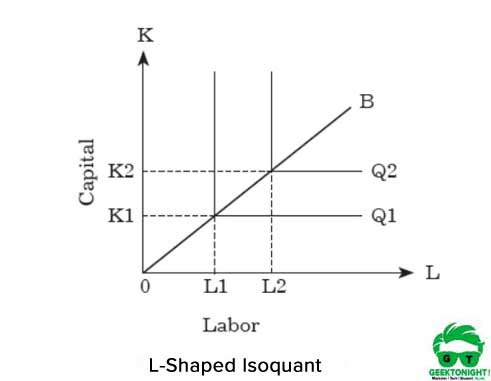
図5に示すように、L字型の等量は、労働と資本の間に置換がなく、補完的な商品であると仮定されていることを表しています。 これは、資本のOK1単位と労働のOL1単位は、Q1の生産のために必要とされることがわかります。

一方、生産量をQ1からQ2に増やすには、k1からK2、L1からL2の両方に投入量を増やす必要があります。 この資本と労働の関係は、次のように表すことができます:Q=f(K,L)=min(aK,bL)

q=f(K,l)=min(aK,bL)

ここで、minはQが二つの項aKとbLの下位に等しいことを意味します

例えば、ａｋ＜１ ７ １ １＞ＢＬの場合、Ｑ＝ＢＬであり、ＡＫ＜４ ５ ７ ２＞ＢＬの場合、Ｑ＝ＡＫである。

このisoquantはleontifの生産機能と同じです。

因子間の置換の弾力性

MRTSは等量の傾きであることがわかります。 しかし、ある因子の別の因子への置換可能性の程度は明らかにされていない。 2つの入力の間の置換可能性の程度を測定することが重要です。

したがって、経済学者は、因子置換の弾力性として知られている二つの入力、資本と労働の間の置換可能性の程度を推定するための式を開発した。

因子置換の弾力性（ε）は、MRTの変化率に対する資本-労働比の変化率の比率を指す。

それは数学的に次のように表されます：

σ=資本労働率の変化率/MRTの変化率

または,

σ K/∆L=MR MRTSの場合、σ=*

; σ=1

高弾性の代替要因との要因を簡単に置換され互いに、”低弾性”を併せ持つことを示す置換の要因が可能である。

線形等量の場合、置換弾性は無限になり、L字型等量の場合はゼロになります。

ISOコスト曲線

Isoコスト曲線は、これらの入力の価格を考えると、組織が採用できる労働と資本のすべての異なる組み合わせの点の軌跡です。 Isoコストラインは、組織が要因に費やす意思がある金額と一緒に要因の価格を表します。

つまり、一定の金額で購入できる要素の組み合わせが異なることを示しています。 Isoコストラインの傾きは、資本の価格に対する労働価格の比率に依存します。

例えば、生産者は総予算が120ドルであり、生産要素、すなわちXとYに費やしたいと考えています。 表7.5は、組み合わせを示しています:

組み合わせ	Xの単位	Yの単位	総支出
A	8	0	120
B	6	3	120
C	4	6	120
D	2	9	120
E	0	12	120

iso-costラインを図7.8に示します:

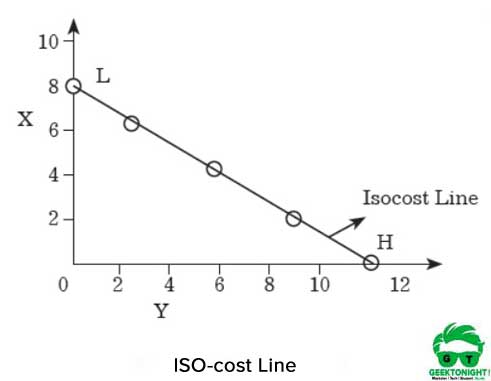
図6に示すように、プロデューサーがXを購入するために全体の金額を費やしている場合、彼/彼女はXの8単位を購入することができます。

点HとLがそれぞれX軸とY軸上に結合されている場合、直線が得られ、これはiso-cost lineと呼ばれます。 この行にあるXとYのすべての組み合わせは、cost120と同じ量のコストを持つことになります。

同様に、生産者が生産要素により多くの金額を費やす意思がある場合に備えて、他のisoコストラインを120以上のコストを取ることによってプロット

isoquantとiso-costラインの助けを借りて、生産者は最小コストを負担することによって入力が最大利益をもたらすポイントを決定することができます。 このような点は生産者の平衡と呼ばれます。

も読む: 枢機卿と序数ユーティリティ

ビジネス経済チュートリアル

（読むにはトピックをクリックしてください)

上に行く、友人と記事を共有