31ACT数学の公式あなたが知っておく必要があります

平面幾何学

角度と線

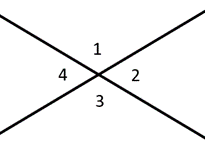
線に沿った角度は補助角度と呼ばれ、合計は\(180^{\circ}\)になります。 補完的な角度は、直角である\(90^{\circ}\)まで加算されます。 垂直角度は、互いに直接向かい合う角度を記述し、常に合同である。 たとえば、左の図では、角度1&2は補助的なものであり、角度1&3は垂直な角度であるとします。

三角形の面積

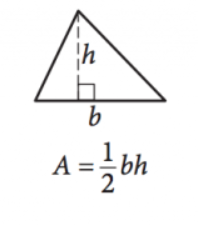
この方程式は、底辺\((b)\)と高さ\((h)\)の長さを与えられた任意の三角形の面積\((A)\)を提供します。 高さは、任意の側（ベース）からその側の真向かいの点/角度までの相補的な角度で伸びる線の長さであることに注意してください。 3辺\((s)\)が同じ長さである正三角形の場合、面積方程式は次のようになります。: \(\Frac{s^2\sqrt{3}}{4}=A\)を計算すると、次のようになります。\(\frac{s^2\sqrt{3}}{4}=A\)を計算すると、次のようになります。\(\frac{s^2\sqrt{3}}{4}=A\)を計算すると、\(\frac{s^2\

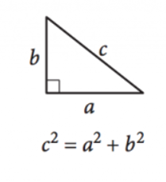
三角形の角度は常に\(180^{\circ}\)に加算されるので、直角三角形は1つの直角を持つ任意の三角形として定義され、他の2つの角度が相補的であることを確 直角三角形の辺の長さは、ピタゴラスの定理によって定義することができます: \(A^2+b^2=c)\(a^2+b^2=c)\(a^2+b^2=c)\(a^2+b^2=c)^2\)

ここで、\(a\)と\(b\)は脚の長さ、または相補的な角度の反対側の辺、\(c\)は斜辺の長さ、直角の反対側の辺です。\(a\)と\(b\)は、\(a\)と\(b\)は、\(a\)と\(b\)は、\(a\)と\(b\)は、\(

次のピタゴラスのトリプル、または辺の長さ\((a,b,c))の値も暗記すると便利です)\): 3-4-5, 5-12-13, 7-24-25, 8-15-17 斜辺は常に最長辺であることに注意してください。

特殊な直角三角形

特殊な直角三角形には、次のような角度と長さの比を持つ二つのタイプがあります:

この式は、長さ\(l\)と幅\(w\)の長方形の面積を提供します。\(A=lw\)と\(a=lw\)の面積を提供します。\(a=lw\)と\(a=lw\)の面積を提供します。\(a=lw\)と\(a=lw\)と\(a=lw\)の面積を提供します。\(a=lw\)と\(a=lw\)の面積を提供します。\(a=lw\)と\(a=lw\)の面積を提供します

\(a=bh\)

この式は、底辺\(b\)が与えられた平行四辺形の面積、最長辺の長さ、高さ\(h\)を提供し、一方の底辺から他方の底辺まで相補的な角度で伸びる線の長さと定義されます。 Frac a=\frac{b_1+b_2}{2}\:\times\frac{b_1+b_2}{2}timesとなります。\:この式は、平行四辺形の場合と同じように定義された、底辺\(b_1\)と\(b_2\)と高さ\(h\)を持つ台形の面積を提供します。正多角形の内角

\((n-2)\:\times\:180^{\circ}=S\)

すべての辺と角度が等しい正多角形では、この式は、\(N\)辺と角度を持つ多角形が与えられた内角の和\((S)\)を提供します。\(N\)辺と角度を持つ多角形が与えられた内角の和を提供します。\(N\)辺と角度を持つ多角形が与えられた内角の和を提供します。\(N\)辺と角度を持つ多角形が与えられた内角の和を提供します。\(N\)辺と角度を持つ多角形が与えられた内角の和を提供します。\(N\)辺と角度を持つ 我々はまた、\(\frac{S}{n}\)を計算することによって各内角を見つけることができます。

円の円弧の長さ

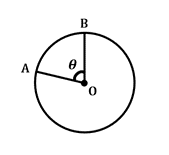
\(\frac frac{\theta}{360^{\circ}}\:\times\theta{はfrac360^{\circ}}で囲まれています。\:2\pi r=arc\:length\)

この式は、円の中心で中心角\(\theta\)で交差する2つの与えられた半径の間の円弧または円の円周のセクションの長さを定義します。\pi r=arc\:length\)

この式は、円の中心で交差する2つの与えられた半径の間の円弧または円の円周のセクションを定義します。 \(2\pi r\)は、この式に円の円周を組み込んでいることに注意してください。 円のセクター面積

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2=sector\:area\)

円弧の長さと同様に、この式は円の中心で交差する2つの与えられた半径の間のセクターの面積を中心角で提供します。 \(\Pi r^2\)は、円の面積をこの式に組み込みます。

3Dシェイプ

\(SA=2(lw+wh+lh)\)

\(これらの式は、長さ\(l\)、幅\(w\)、高さ\(h\)の矩形プリズムの表面積\((SA)\)と体積\((V)\)を提供します。

\(V=\pi r^2h\)

この式の右シリンダーベースradius\(r\)と高さ\(h).

他の3D形状の表面積または体積の式が必要な場合、ACTは質問自体に関連する式を提供します。 三角法

SOH-CAH-TOA

ほとんどのACT三角問題は、直角三角形の与えられた角度\（x\）に対して次のように計算される正弦、余弦、および正接を操作することを含みます。

\（sin（x）=\frac{反対\：脚}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}\)

\(cos（x）=\frac{隣接する\：脚}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}{斜辺}\)

\(tan（x）=\frac{反対側の\：脚}{隣接した\：脚}=\frac{sin（x）}{cos（x）}cosとなります。)}\)

SOH-CAH-TOAは、どのtrig関数がどの辺の長さに対応するかを覚えておくための簡単なニーモニックです！Co sin(x)=cos(90^{\circ}-x-とすると、Co sin(x)=cos(90^{\circ}-x-となります。)\)

\(つまり、これらの恒等式は、角度\(x\)の三角関数が\(x\)の補数の共関数の値に等しいことを示しています。 それらは一般に、より高度な三角法を扱うときに使用され、正弦と余弦の間の簡単な変換を可能にします。\(Sin(x)\),\(cos(x)\),\(tan(x)\)の逆数の恒等式を見ることができます。\(\sin(x)\)と\(\cos(x)\)の逆数の恒等式を見ることができます。:

\（csc（x）=\frac{1}{sin（x）}）sinです。)}\)

\(sec sec（x）=\frac{1}{cos（x）}sec)}\)

\(cot（x）=\frac{1}{tan（x）}tanとなります。)}\)

ピタゴラスの恒等式

\(sin^2(x)+cos^2(x))\(723)\(3997)\(3997)\)=1\)

ピタゴラスの定理と単位円に基づいて、この恒等式は一般に、角度\(x\)または\(x\)のこれらの三角関数の値が不明であるtrig問題（sans電卓）を解決するために余関数恒等式と一緒に使用される。 Statistics m=\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100}\times\frac{n}{100\:M\)

パーセンテージは全体の一部を表現するために使用され、\(\%\)記号は一般的に「100で割る」ことを意味します。 したがって、上記の式は、量\(m\)の\(n\%\)を求める問題に答えます。

平均値、中央値、モード、および範囲

ACTは、基本的な統計的知識をテストします。:

• Meanは平均、または\(\frac{sum\:of\:all\:terms}{total\:number\:of\:条件}\)
• 中央値は、中長期の平均の中規約がある場合でも数
• モードでの期間(s)に発生する頻度の高い
• の範囲の違いを最大と最小の条件

確率

\(P(A)=\frac{数字\:そ:希望\:成果}{合計数\:りすることができる\:成果}\)

確率を表す可能性のイベント\((A)\)発生して計算した数で除し望ましい成果の数は合計できます。 たとえば、偶数面のサイコロに6を転がす確率は\(\frac{1}{6}\)です。\(A\)と\(b\)は、\(a\)が発生しても\(B\)が発生する確率に影響しない場合、\(P(A\)と\(b\)は独立しています。\(p(a\)と\(b\)は独立しています。\(p(a\)と\(b\)は独立しています。\(p(a\)と\(b\)は独立しています。\(p(a\)と\(b\)は独立しています。\(p(a\)と\(b\)は独立しています。\(p(a\)と\(b\)は独立しています。\(p(a\)と\(b\)は独立しています。\(p( 両方の独立したイベントが発生する確率を計算するために、それらの個々の確率を乗算します。 たとえば、ヘッドを2回反転する確率は\(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\)です。

それをラップ

この記事では多くの数式を取り上げましたが、代数IIと幾何学を通してすべての数学の概念を見直すようにしてください！ たとえば、複素数、ベクトル、行列、方程式系、およびグラフィカル関数の操作も同様にテストされることが期待できます。 詳細については、ACT mathセクションのこの完全な説明を参照してください。

練習は、特に数学のために完璧になることを覚えておいてください！ あなたは本当にタイムリーにこれらの概念や数式を適用し、統合する方法を理解することを目標に、テスト日の前にさまざまな問題の多くを試してみ

あなたは行為のための計算機を許可されているので、我々はそれを持って来ることをお勧めしますが、注意の言葉で。 すべての行為の数学の問題は、電卓なしで解決することができ、それはあなたが実際にする必要はありませんときにあなたの電卓を使用して、貴重 あなたがいずれかを持参することを計画している場合は、そのように、あなたの電卓で時限練習セクションを行い、それが最後の手段としてのみ: 計算を容易にし、あなたの速度を向上させるために。 それのためにまれに達し、あなたの特定のモデルが行為の計算機の方針に従って許可されることを確認して下さい。