31 ACT Matematiske Formler Du Trenger Å Vite

Plane Geometry

Vinkler Og Linjer

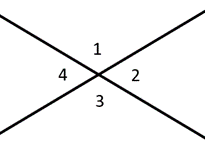
Vinkler langs en linje kalles supplerende vinkler, legger opp til \(180^{\circ}\). Komplementære vinkler legger opp til \(90^{\circ}\), en rett vinkel. Vertikale vinkler beskriver vinkler rett overfor hverandre, som alltid er kongruente. I diagrammet til venstre vil vi for eksempel si at vinkler 1 & 2 er supplerende, mens vinkler 1 & 3 er vertikale vinkler.

Område Av En Trekant

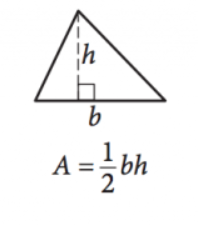
Bilde gjengitt av SAT

\(\frac{1}{2}bh=A\)

denne ligningen gir området \((A)\) av en hvilken som helst trekant gitt lengder av basen \((b)\) og høyde \((h)\). Merk at høyden er lengden på linjen som strekker seg i en komplementær vinkel fra hvilken som helst side (basen) opp til punktet/vinkelen rett over fra den siden.

for like-sidige trekanter, hvor alle tre sidene \((s)\) er like lange, er arealligningen:

\(\frac{s^2 \ sqrt{3}}{4}=A\)

Pythagorasetningen

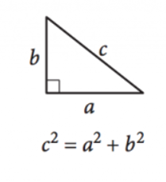
Bilde gjengitt av SAT

som vinkler i en trekant alltid legge opp til \(180^{\circ}\), er en rettvinklet trekant definert som en trekant med en rett vinkel, sikre de to andre vinklene er komplementære. Sidelengder av høyre trekanter kan defineres Av Pythagoras ‘ Læresetning:

\(a^2 + b^2 = c^2\)

Her er \(a\) og\ (b\) lengdene på bena, eller sidene over fra de komplementære vinklene, og \(c\) er lengden på hypotenusen, siden over fra den rette vinkelen.

det kan være nyttig å også huske Følgende Pythagoranske tripler,eller verdier for sidelengder \((a, b, c)\): 3-4-5, 5-12-13, 7-24-25, og 8-15-17. Legg merke til at hypotenusen alltid er den lengste siden.

Spesielle Høyre Trekanter

det finnes to typer spesielle høyre trekanter, som har vinkler og lengdeforhold som følger:

Bilde gjengitt av SAT

Områder Av Quadrilaterals

\(a = lw\)

denne formelen gir arealet av et rektangel med lengde \(l\) og bredde \(w\).

\(a = bh\)

denne formelen gir arealet av et parallellogram gitt base \(b\), lengden på de lengste sidene og høyden \(h\), definert som lengden på linjen som strekker seg i en komplementær vinkel opp fra en base til den andre.

\(a=\frac{b_1 + b_2}{2}\: \ ganger\:h\)

denne formelen gir arealet av et trapes med baser \(b_1\) og \(b_2\) og høyde \(h\), definert på samme måte som for parallellogrammer.

Indre Vinkler Av Regulære Polygoner

\((n-2)\: \ times\: 180^{\circ}= S\)

i et regulært polygon, hvor alle sider og vinkler er like, gir denne formelen summen \(S)\) av de indre vinklene gitt et polygon med \(n\) sider og vinkler. Vi kan også finne hver indre vinkel ved å beregne \(\frac{s}{n}\).

Buelengde I En Sirkel

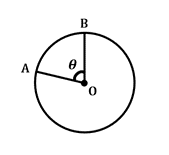
\(\frac {\theta}{360^{\circ}}\: \ ganger\:2\pi r=arc\: length\)

denne formelen definerer lengden på buen, eller delen av sirkelomkretsen, mellom to gitte radier som skjærer i sirkelsenteret med sentral vinkel \(\theta\). Merk at \(2 \ pi r\) inkorporerer sirkelomkrets i denne formelen.

Sektorområde i En Sirkel

\(\frac{\theta}{360^{\circ}}\: \ times\: \ pi r^2 = sektor\: område\)

I Likhet med buelengde gir denne formelen arealet av sektoren mellom to gitte radier som skjærer i sirkelsenteret med sentral vinkel . \(\Pi r^2\) inkorporerer sirkelområdet i denne formelen.

3d-Figurer

\(SA = 2 ( lw + wh + lh)\)

\(V= lwh\)

disse formlene gir overflatearealet \((sa)\) og volum \((V)\) for et rektangulært prisme med lengde \(l\), bredde \(w\) og høyde \(h\).

\(V=\pi r^2h\)

dette er volumformelen for en høyre sylinder med baseradius \(r\) og høyde \(h\).

hvis du trenger overflatearealet eller volumformlene for andre 3d-figurer, vil ACT gi relevante formler i selve spørsmålene.

Trigonometri

SOH-CAH-TOA

DE FLESTE ACT trig-problemer involverer manipulering av sinus, cosinus og tangent, som beregnes som følger for gitt vinkel \(x\) i en riktig trekant:

\(sin(x)=\frac{motsatt\:leg}{hypotenuse}\)

\(cos (x)= \ frac{tilstøtende\: leg}{hypotenuse}\)

\(tan (x)=\frac{motsatt\:leg}{tilstøtende\:leg} = \frac{sin(x)}{cos (x)}\)

SOH-CAH-TOA er en enkel mnemonic for a huske hvilken trig-funksjon som tilsvarer hvilke sidelengder!

Kofunksjonsidentiteter

\(sin(x) = cos (90^{\circ} – x)\)

\(cos (x) = sin (90^{\circ}-x)\)

i ord viser disse identitetene at en trig-funksjon av vinkel \(x\) er lik verdien av kofunksjonen av komplementet til \(x\). De brukes vanligvis når du arbeider med mer avansert trigonometri, noe som åpner for enkle konverteringer mellom sinus og cosinus.

Ratio / Gjensidige Trig Identiteter

du kan av Og til se gjensidige identiteter av \(sin(x)\), \(cos(x)\), og \(tan(x)\), som er:

\(csc(x) =\frac{1}{sin(x)}\)

\(seg(x) = \frac{1}{cos (x)}\)

\(cot (x) = \frac{1}{tan (x)}\)

Pythagoras Identitet

\(sin^2 (x) + cos^2 (x)=1\)

Basert På Pythagoras ‘ Læresetning og enhetssirkelen, er denne identiteten vanligvis brukt sammen med cofunction identiteter for å løse trig problemer (sans kalkulator) hvor vinkel \(x\) eller verdiene av disse trig funksjoner av \(x\) er ukjent.

Statistikk Og Sannsynlighet

Prosenter

\(n\%\: av\: m = \frac{n}{100}\:\ganger\:M\)

Prosenter brukes til å uttrykke deler av en helhet, og \(\%\) symbolet betyr vanligvis ” dividere med 100.”Som sådan svarer ovennevnte ligning ethvert problem som ber om \(n\%\) av kvantitet \(m\).

Gjennomsnitt, Median, Modus Og Rekkevidde

ACT tester grunnleggende statistisk kunnskap, vanligvis med tiltakene nedenfor:

• Gjennomsnitt er gjennomsnittet, eller \(\frac{sum\: of\: all\: terms}{total\: number\: of\:vilkår}\)
• median er mellomtermen, eller gjennomsnittet av de to mellomtermene hvis det er et jevnt antall vilkår
• Modus Er termen(e) som forekommer hyppigst
• Området Er forskjellen mellom de største og minste vilkårene

Sannsynlighet

\(P(A) = \frac{tall\:of\:desired\:outcomes}{total\:number\:of\:possible\:outcomes}\)

sannsynlighet representerer sannsynligheten for at en hendelse \(a)\) forekommer, beregnet ved å dividere antall ønskede utfall med antall totale mulige utfall. For eksempel er sannsynligheten for å rulle en 6 på en jevn terning \(\frac{1} {6}\).

Uavhengige Hendelser

\(P (a\: og\: B) = P(a)\: \ ganger\: P (B)\)

Hendelser\ (a\) og\ (B\) er uavhengige hvis\ (A\) inntreffer ikke påvirker sannsynligheten for \(B\) inntreffer. For å beregne sannsynligheten for at begge uavhengige hendelser vil oppstå, multipliserer vi deres individuelle sannsynligheter sammen. For eksempel er sannsynligheten for å vende hodene to ganger \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

Innpakning Det Opp

Vi har dekket mange formler i dette innlegget, Men sørg for å også gjennomgå alle matematiske begreper Gjennom Algebra II og Geometri! For eksempel kan du forvente komplekse tall, vektorer, matriser, ligningssystemer og manipulere grafiske funksjoner for å være på prøve også. Se denne fullstendige beskrivelsen AV ACT math-delen for mer info.

Husk at praksis gjør mester, spesielt for matte! Du vil prøve mange forskjellige problemer før testdagen, med målet om å virkelig forstå hvordan du søker og integrerer disse konseptene og formlene i tide.

som du har lov til en kalkulator FOR LOVEN, vil vi anbefale å bringe en, men med et ord av forsiktighet. Husk at HVER ACT math problem kan løses uten en kalkulator, og det er lett å kaste bort verdifull tid ved å bruke kalkulatoren når du faktisk ikke trenger å. Som sådan, gjør tidsbestemt praksis seksjoner med kalkulatoren din hvis du planlegger å ta med en, og husk at det bare er der som en siste utvei: for å lette beregninger og øke hastigheten. Reach for det sjelden, og sjekk at din spesifikke modell er tillatt per ACT kalkulator politikk.