Isoquant Kurve: Definisjon, Egenskaper, Typer, Forutsetninger
Hva Er Isoquant Curve?
Isoquant Kurve: en teknisk relasjon som viser hvordan input konverteres til output er avbildet av en isoquant kurve. Den viser de optimale kombinasjonene av faktorinnganger ved hjelp av priser på faktorinnganger og deres mengder som brukes til å produsere samme utgang.
BEGREPET ISO innebærer lik og quant betyr mengde eller utgang.
for eksempel, for å produsere 100 kalendere, brukes 90 kapitalenheter og 10 arbeidsenheter.
Isokvante kurver kalles også som like produktkurver eller produksjons likegyldighetskurver.
Definisjon Av Isokvant Kurve
Forutsetninger For Isoquant Kurve
forutsetningene for en isoquant kurve er som følger:
- det er bare to faktorinnganger, arbeidskraft og kapital, for å produsere et bestemt produkt.
- Kapital, arbeid og varer er delbare i naturen.
- Kapital og arbeidskraft kan erstatte hverandre opp til en viss grense.
- Produksjonsteknologi er gitt over en tidsperiode.
- Produksjonsfaktorer brukes med full effektivitet.
La oss lære isoquant ved hjelp av følgende tabell.
Tabell 1 viser de ulike kombinasjonene av tofaktorinnsats, nemlig arbeidskraft og kapital for produksjon av 150 tonn produksjon:
| Arbeid | Kapital |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
Figur 1 viser den isokvante kurven for ulike arbeidskapitalkombinasjoner som bidrar til å produsere 150 tonn produksjon:
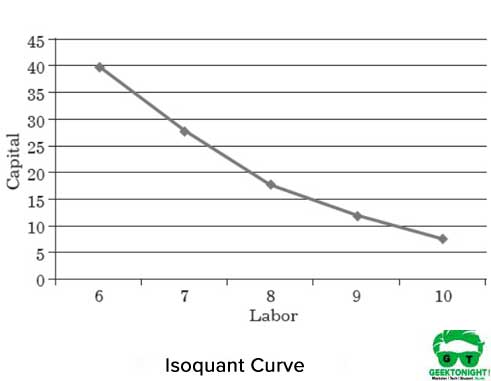
Egenskaper Av Isoquant Kurve
noen av egenskapene til isoquant kurve er som følger:
- Isoquant kurver skråning nedover
- Isoquant kurver er konvekse til opprinnelse
- Isoquant kurver kan ikke krysse hverandre
- Høyere isoquant jo høyere utgang

Isoquant kurver skråning nedover
det innebærer at skråningen av isoquant kurven er negativ. Dette skyldes at når kapitalen (K) økes, reduseres mengden arbeidskraft (L) eller omvendt, for å holde samme produksjonsnivå.
Isoquant kurver er konvekse til opprinnelse
det innebærer at faktorinnganger ikke er perfekte erstatninger. Denne egenskapen viser substitusjon av innganger og redusert marginal rate av teknisk substitusjon av isoquant. Den marginale betydningen av en input (kapital) i form av en annen input (arbeidskraft) reduseres sammen med isoquant-kurven.
Figur 2 viser den konvekse isoquant kurve:
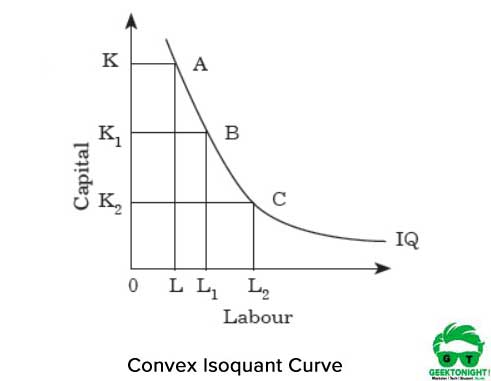
konveksiteten representerer AT MRTS reduseres hvis vi beveger oss fra punkt A Til B og Fra B til C langs isoquanten. MRTS reduseres fordi de to innsatsene arbeidskraft og kapital ikke er perfekte erstatninger.
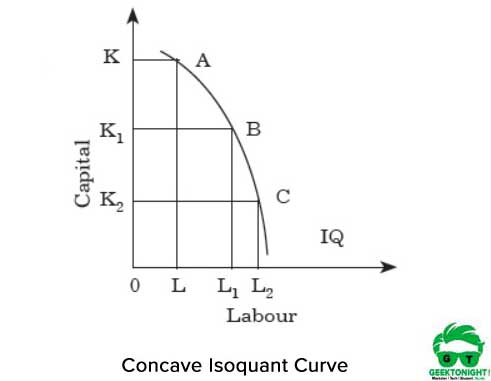
for hver økning i arbeidskraft er det således en nedgang i kapital. Hvis isoquant er konkav, ØKER MRT av arbeidskraft for kapital. Figur 3 viser den konkave isokvantkurven:
som vist i Figur 3, hvis VI beveger oss fra punkt A til B og fra B til C langs isokvanten, øker MRTS. Det viser at de to innsatsene arbeidskraft og kapital er perfekte erstatninger. Dermed er det for hver økning i arbeidskraft en økning i kapital.
Isoquant kurver kan ikke krysse hverandre
en isoquant innebærer de forskjellige nivåene av kombinasjon som produserer forskjellige nivåer av innganger. Hvis isokvantene krysser hverandre, vil det innebære at en enkelt inngangskombinasjon kan produsere to nivåer av utgang, noe som ikke er mulig. Produksjonsloven vil ikke være anvendelig.
Høyere isoquant jo høyere utgang
det innebærer at høyere isoquant representerer høyere utgang. Den øvre kurven av isoquant produserer mer utgang enn kurven under. Dette skyldes at den større kombinasjonen av input resulterer i en større utgang i forhold til kurven som er under den.
Marginal Rate Of Technical Substitution
hellingen til isoquant-kurven er substitusjonsraten som viser hvordan en inngang kan erstattes av en annen mens du holder utgangskonstanten. Dette kalles marginal rate of technical substitution (MRT).
Ifølge Lipsey, ” den marginale frekvensen av teknisk substitusjon kan defineres som hastigheten der en faktor er erstattet av en annen med utgang holdt konstant.”
formelen FOR beregning AV MRT er som følger:
MRTS = – ∆K / HRYVNIAS l
hvor, ∆K = Endring i kapital
∆l= Endring i arbeidskraft
formelen viser at PÅ et gitt produksjonsnivå vil MRTS av kapital for arbeidskraft innebære mengden arbeidskraft som firmaet ville være villig til å gi opp for en ekstra kapitalenhet. TILSVARENDE VIL MRTS av arbeidskraft for kapital innebære mengden kapital som firmaet ville være villig til å gi opp for en ekstra arbeidsenhet.
MRTS er også lik forholdet mellom marginalprodukt av en inngang til marginalproduktet av en annen inngang. Utgangen langs isoquanten er konstant. Hvis endringen i arbeidskraft er erstattet av kapitalendringen, bør økningen i produksjonen på grunn av økt arbeidskraft samsvare med nedgangen i produksjonen på grunn av nedgang i kapital. Matematisk
∆L x (MPL)= ∆K x MPk
∆Q= ∆L x (MPL) + ∆K x MPk
Siden utgangen forblir uendret på et gitt isoquant,
∆L x (MPL) + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
Dermed kan vi si at MRTS mellom inngangene er lik marginal produkter av innganger.
MRTENE beregnes som vist I Tabell 2
| Arbeidskraft | Kapital | MRT |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
Typer Isokvant Kurve
det er en kontinuerlig substitusjon av en inngangsvariabel med den andre inngangsvariabelen med en avtagende hastighet. Perfekte komplementer og perfekte erstatninger gir forskjellige former for isoquants.
de forskjellige typene isoquant kurve er som følger:
- Lineær isokvant
- l-formet isokvant

Lineær isoquant
Det er en rett linje isoquant og representerer en perfekt substituerbarhet mellom input, kapital og arbeid i produksjonsfunksjonen. MRT mellom innganger forblir konstant. Figur 4 viser en lineær isoquant:
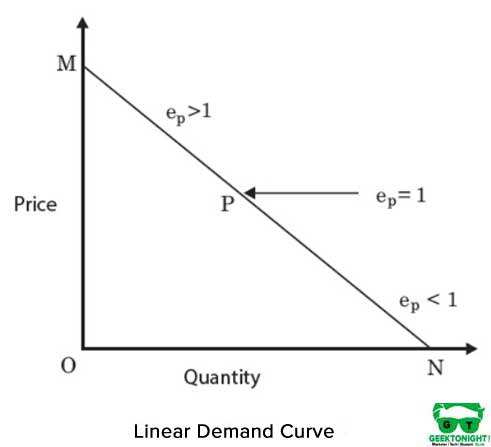
den algebraiske form for produksjonsfunksjon i tilfelle lineær isoquant er som følger:
Q = aK + BL
Her Er Q den vektede summen Av K Og L. kurvens helling kan beregnes ved hjelp av følgende formel:
MPK = ∆Q/∆K = a
MPL = ∆Q / ∆l = b
MRTS = MPL/MPK
MRTS = -b/a (b / A er konstant)
lineær isoquant eksisterer imidlertid ikke i den virkelige verden.
L-formet isoquant
dette er tilfelle av perfekte komplementer. Under dette er kombinasjonen mellom kapital og arbeidskraft i en fast andel. Bare en kombinasjon av arbeidskraft og kapital er mulig å produsere et produkt med festet andel av innsatsfaktorer.
for å øke produksjonen må en organisasjon øke begge innsatsene proporsjonalt. Den grafiske representasjon av fast faktor andel isoquant Er L i form, vist I Figur 5:
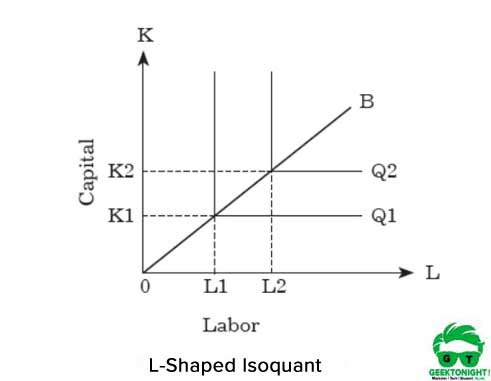
som vist i Figur 5 representerer den L-formede isokanten at det ikke er noen erstatning mellom arbeidskraft og kapital, og de antas å være komplementære varer. DET kan sees AT OK1 enheter av kapital og OL1 enheter av arbeidskraft er nødvendig for produksjon Av Q1.
på den annen side, for å øke produksjonen Fra Q1 Til Q2, må en organisasjon øke innsatsene Fra K1 Til K2 og L1 til L2 begge. Dette forholdet mellom kapital og arbeidskraft kan uttrykkes som følger:
Q = f (K, L) = min (aK, bL)
hvor, min innebærer Q er lik til lavere av de to termene, aK og bL
For eksempel, i tilfelle aK > bL, Så Q = bL og i tilfelle aK < bL så, Q = aK.
denne isoquant er samme som leontif produksjonsfunksjon.
Elasticitet Av Substitusjon Mellom Faktorer
VI vet AT MRT er skråningen til isoquanten. Det avslører imidlertid ikke graden av substituerbarhet av en faktor til en annen. Det er viktig å måle graden av substituerbarhet mellom de to inngangene.
derfor har økonomer utviklet en formel for å estimere omfanget av substituerbarhet mellom de to innsatsene, kapital og arbeidskraft, som er kjent som elastisitet av faktorsubstitusjon.
Elasticitet av faktorsubstitusjon (σ) refererer til forholdet mellom prosentvis endring i kapital-arbeidsforhold og prosentvis endring i MRT.
det er matematisk representert som følger:
σ = prosentvis endring i kapitalarbeidsforhold / PROSENTVIS endring i MRT
Eller,
σ = *
Hvis ∆K / ∆L = ∆ ; σ = 1
Hvis ∆K/∆L > ∆MRTS ; σ > 1
Hvis ∆K/∆L < ∆MRTS ; σ < 1
Høy elastisitet av substitusjon mellom faktorer innebærer at faktorer kan lett byttes ut med hverandre, mens en lav elastisitet representerer at substitusjon av faktorer som er mulig til en viss grad.
ved lineær isoquant vil substitusjonselasticiteten være uendelig, og I Tilfelle L-formede isoquants vil den være null.
ISO-Kostnadskurver
Iso-kostnadskurve er stedet for poeng for alle forskjellige kombinasjoner av arbeidskraft og kapital som en organisasjon kan ansette, gitt prisen på disse innsatsfaktorene. Iso-kostnadslinjen representerer prisen på faktorer sammen med hvor mye penger en organisasjon er villig til å bruke på faktorer.
med andre ord viser det forskjellige kombinasjoner av faktorer som kan kjøpes til en viss sum penger. Skråningen på iso-kostnadslinjen avhenger av forholdet mellom prisen på arbeidskraft og prisen på kapital.
for eksempel har en produsent et totalt budsjett på ₹120, som han ønsker å bruke på produksjonsfaktorene, Nemlig X Og Y. prisen På X i markedet er ₹15 per enhet og Prisen På Y er ₹10 per enhet. Tabell 7.5 viser kombinasjonene:
| Kombinasjoner | Enheter Av X | Enheter Av Y | Totale utgifter |
|---|---|---|---|
| A | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
iso-kostnadslinjen er vist i Figur 7.8:
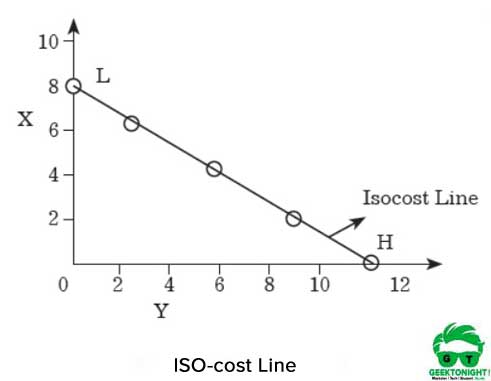
som vist i Figur 6, hvis produsenten bruker hele beløpet Til å kjøpe X, kan han / hun kjøpe 8 enheter Av X. På den annen side, hvis produsenten kjøper Y Med hele beløpet, vil han / hun kunne få 12 enheter.
hvis punktene H og L er sammenføyet på Henholdsvis x-og Y-akser, oppnås en rett linje, som kalles iso-kostnadslinje. Alle kombinasjonene Av X og Y som ligger på denne linjen, vil ha samme beløp som er ₹120.
på Samme måte kan andre iso-kostnadslinjer tegnes ved å ta koster mer enn 120, dersom produsenten er villig til å bruke mer penger på produksjonsfaktorene.
ved hjelp av isoquant og iso-kostnadslinjer kan en produsent bestemme punktet hvor innganger gir maksimal fortjeneste ved å pådra seg minimumskostnad. Et slikt punkt kalles produsentens likevekt.
Les Også: Cardinal Og Ordinal Utility
Bedriftsøkonomi Tutorial
(Klikk På Emnet For Å Lese)
Fortsett, Del artikkel med Venner
Leave a Reply