31 wiskundige formules die u moet kennen

vlakke geometrie

hoeken en lijnen

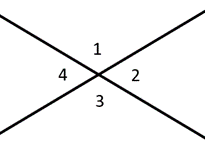
hoeken langs een lijn worden aanvullende hoeken genoemd, die optellen tot \(180^{\circ}\). Complementaire hoeken tellen op tot \(90^{\circ}\), een rechte hoek. Verticale hoeken beschrijven hoeken direct tegenover elkaar, die altijd congruent zijn. In het diagram links zouden we bijvoorbeeld zeggen dat hoeken 1 & 2 aanvullend zijn, terwijl hoeken 1 & 3 verticale hoeken zijn.

oppervlakte van een driehoek

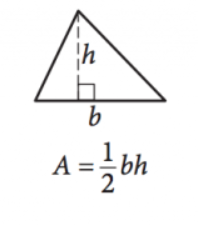
figuur met dank aan SAT

\(\frac{1}{2}bh=A\)

deze vergelijking geeft de oppervlakte \((a)\) van elke driehoek gegeven lengtes van de basis \((b)\) en hoogte \((h)\). Merk op dat de hoogte de lengte is van de lijn die zich onder een complementaire hoek uitstrekt vanaf elke zijde (de basis) tot aan het punt/de hoek direct tegenover die zijde.

voor gelijkzijdige driehoeken, waarbij alle drie zijden \((s)\) dezelfde lengte hebben, is de gebiedsvergelijking:

\(\frac{s^2\sqrt{3}}{4} = A\)

Stelling van Pythagoras

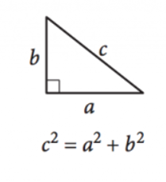
figuur met dank aan SAT

omdat hoeken in een driehoek altijd optellen tot \(180^{\circ}\), wordt een rechthoekige driehoek gedefinieerd als elke driehoek met één rechte hoek, zodat de andere twee hoeken elkaar aanvullen. De zijlengtes van rechthoekige driehoeken kunnen worden gedefinieerd door de Stelling van Pythagoras:

\(a^2+b^2 = c^2\)

hier zijn \(A\) en \(b\) de lengtes van de benen, of de zijkanten tegenover de complementaire hoeken, en \(c\) is de lengte van de hypotenusa, de zijde tegenover de rechte hoek.

het kan nuttig zijn om ook de volgende Pythagorese triples, of waarden voor zijlengtes \((a,b, c)\): 3-4-5, 5-12-13, 7-24-25, en 8-15-17. Merk op dat de hypotenusa altijd de langste zijde is.

speciale rechthoekige driehoeken

er zijn twee soorten speciale rechthoekige driehoeken, die de hoeken en lengteverhoudingen als volgt hebben::

figuur met dank aan SAT

gebieden van Quadrilateralen

\(A = lw\)

deze formule geeft de oppervlakte van een rechthoek met lengte \(l\) en breedte \(w\).

\(A = bh\)

deze formule geeft de oppervlakte van een parallellogram gegeven basis \(b\), de lengte van de langste zijden en hoogte \(h\), gedefinieerd als de lengte van de lijn die zich onder een complementaire hoek uitstrekt van de ene basis naar de andere.

\(A = \frac{b_1+b_2}{2}\: \ times\:h\)

deze formule geeft de oppervlakte van een trapezium met basen \(b_1\) en \(b_2\) en hoogte \(h\), gedefinieerd op dezelfde manier als voor parallelogrammen.

binnenhoeken van regelmatige veelhoeken

\((n-2)\:\times\: 180^{\circ}= s\)

In een regelmatige veelhoek, waar alle zijden en hoeken gelijk zijn, levert deze formule de som \(S)\) van de binnenhoeken gegeven een veelhoek met \ (n\) zijden en hoeken. We kunnen ook elke inwendige hoek vinden door \(\frac{s}{n}\) te berekenen.

booglengte in een cirkel

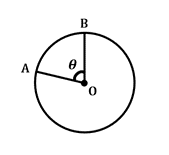
\(\frac {\theta}{360^{\circ}}\: \ times\:2 \ pi r = arc\: Lengte\)

deze formule definieert de lengte van de boog, of sectie van de cirkelomtrek, tussen twee gegeven radii die snijden in het cirkelcentrum met centrale hoek \(\theta\). Merk op dat de \(2\pi r\) cirkelomtrek in deze formule opneemt.

Sectorgebied in een cirkel

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = sector\: area\)

vergelijkbaar met booglengte, geeft deze formule het gebied van de sector tussen twee gegeven radii die elkaar snijden in het centrum van de cirkel met centrale hoek . De\ (\pi R^2\) neemt het cirkelgebied in deze formule op.

3D-vormen

\(SA = 2 (lw + wh + lh)\)

\(V= lwh\)

deze formules bieden de oppervlakte \((SA)\) en volume \((V)\) voor een rechthoekig prisma met lengte \(l\), breedte \(w\) en hoogte \(h\).

\(V= \ pi r^2h\)

Dit is de volumeformule voor een rechtercilinder met basisradius \(r\) en hoogte \(h\).

indien u de oppervlakte-of volumeformules voor andere 3D-vormen nodig hebt, zal de ACT relevante formules in de vragen zelf leveren.

Goniometrie

SOH-CAH-TOA

de Meeste vinden het trig-problemen betrekken bij het manipuleren van sinus, cosinus en tangens, die als volgt worden berekend voor bepaalde hoek \(x\) in een rechthoekige driehoek:

\(sin(x)=\frac{tegenover\:been}{schuine zijde}\)

\(cos(x)=\frac{aangrenzende\:been}{schuine zijde}\)

\(tan(x)=\frac{tegenover\:been}{aangrenzende\:been}=\frac{sin(x)}{cos(x)}\)

SOH-CAH-TOA is een makkelijk ezelsbruggetje voor het onthouden van die goniometrische functie komt overeen met die kant lengtes!

Cofunctionele identiteiten

\(sin ( x) = cos(90^{\circ} – x)\)

\(cos(x) = sin(90^{\circ}-x)\)

in woorden laten deze identiteiten zien dat een trig-functie van hoek \(x\) gelijk is aan de waarde van de cofunctie van het complement van \(x\). Ze worden over het algemeen gebruikt bij het omgaan met meer geavanceerde trigonometrie, waardoor eenvoudige conversies tussen sinus en cosinus.

Ratio / reciproque Trig identiteiten

soms ziet u de reciproque identiteiten van \(sin (x)\), \(cos (x)\), en \(tan (x)\), die zijn:

\(csc (x) = \ frac{1}{sin (x)}\)

\(sec (x) =\frac{1}{cos (x)}\)

\(cot (x) =\frac{1}{tan (x)}\)

Pythagorese identiteit

\(sin^2(x)+cos^2 (x))=1\)

gebaseerd op de Stelling van Pythagoras en de eenheidscirkel, wordt deze identiteit over het algemeen gebruikt naast de cofunctie-identiteiten om trig problemen op te lossen (sans calculator) waar hoek \(x\) of de waarden van deze trig functies van \(x\) onbekend zijn.

statistieken en waarschijnlijkheid

Percentages

\(n\%\: van\: M = \ frac{n}{100}\: \ times\:m\)

Percentages worden gebruikt om delen van een geheel uit te drukken, en het \(\%\) symbool betekent in het algemeen “delen door 100.”Als zodanig beantwoordt de bovenstaande vergelijking elk probleem dat vraagt om \(n\%\) van hoeveelheid \(m\).

gemiddelde, mediaan, modus en bereik

de ACT test statistische basiskennis, waarbij in het algemeen de onderstaande maten worden gebruikt:

• gemiddelde is het gemiddelde, of \(\frac{som\: van\: alle\: termen}{totaal\: aantal\: van\:voorwaarden}\)
• Mediaan is de middelste van de looptijd, of het gemiddelde van de twee middelste termen als er een even aantal voorwaarden
• Modus is de term(en) die vaak optreedt
• Bereik is het verschil tussen de grootste en kleinste voorwaarden

Waarschijnlijkheid

\(P(A) = \frac{getal\:van\:gewenste\:resultaten}{totaal\:number\:van\:mogelijk\:resultaten}\)

Waarschijnlijkheid vertegenwoordigt de waarschijnlijkheid van een gebeurtenis \(A)\) optreedt, wordt berekend door het aantal van de gewenste resultaten door het totale aantal mogelijke uitkomsten. Bijvoorbeeld, de kans om een 6 te rollen op een evenzijdige dobbelsteen is \(\frac{1}{6}\).

onafhankelijke gebeurtenissen

\(P(A\:en\:B) = P(A)\:\times\:P(B)\)

gebeurtenissen \(A\) en \(B\) zijn onafhankelijk als \(a\) optreden geen invloed heeft op de waarschijnlijkheid van \(B\) optreden. Om de waarschijnlijkheid te berekenen dat beide onafhankelijke gebeurtenissen zullen plaatsvinden, vermenigvuldigen we hun individuele waarschijnlijkheden samen. Bijvoorbeeld, de kans om koppen twee keer om te draaien is \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

het afronden

we hebben veel formules behandeld in dit bericht, maar zorg ervoor dat u ook alle wiskundige concepten door middel van Algebra II en meetkunde bekijkt! Je kunt bijvoorbeeld verwachten dat complexe getallen, vectoren, matrices, stelsels van vergelijkingen en het manipuleren van grafische functies ook op de test staan. Zie deze volledige beschrijving van de ACT math sectie voor meer info.

onthoud dat oefenen perfect is, vooral voor wiskunde! U zult veel verschillende problemen willen proberen voor de testdag, met als doel om echt te begrijpen hoe u deze concepten en formules tijdig kunt toepassen en integreren.

aangezien u een rekenmachine voor de handeling mag gebruiken, raden wij u aan er een mee te nemen, maar met een woord van voorzichtigheid. Vergeet niet dat elke ACT wiskunde probleem kan worden opgelost zonder een rekenmachine, en het is gemakkelijk om waardevolle tijd te verspillen met behulp van uw rekenmachine wanneer je eigenlijk niet nodig. Als zodanig, doe getimede praktijk secties met uw rekenmachine als u van plan bent om een te brengen, en vergeet niet dat het er alleen als een laatste redmiddel: om berekeningen te vergemakkelijken en uw snelheid te verhogen. Reach voor het zelden, en controleer of uw specifieke model is toegestaan volgens de wet calculator beleid.