Isoquant Curve: definitie, eigenschappen, typen, aannames
Wat is Isoquant Curve?
Isoquantcurve: een technische relatie die laat zien hoe inputs worden omgezet in output wordt weergegeven door een isoquantcurve. Het toont de optimale combinaties van factorinputs met behulp van de prijzen van factorinputs en hun hoeveelheden die worden gebruikt om dezelfde output te produceren.
de term ISO betekent gelijk en quant betekent hoeveelheid of output.
voor de productie van 100 kalenders worden bijvoorbeeld 90 eenheden kapitaal en 10 eenheden arbeid gebruikt.
Isoquantcurves worden ook wel gelijk productcurves of productieonafhankelijkheidscurves genoemd.
Isoquantcurve definitie
aannames van de Isoquantcurve
de aannames van een isoquantcurve zijn als volgt:
- er zijn slechts twee factoren, arbeid en kapitaal, om een bepaald product te produceren.Kapitaal, arbeid en goederen zijn van nature deelbaar.
- kapitaal en arbeid kunnen elkaar tot een bepaalde limiet vervangen.
- productietechnologie wordt over een bepaalde periode gegeven.
- productiefactoren worden met volledige efficiëntie gebruikt.
laten we isoquant leren met behulp van de volgende tabel.
Tabel 1 geeft de verschillende combinaties van twee-factor inputs, namelijk arbeid en kapitaal voor de productie van 150 ton uitvoer:
| Arbeid | Kapitaal |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
figuur 1 toont de isoquantcurve van verschillende combinaties van arbeidskapitaal die helpen bij het produceren van 150 ton productie:
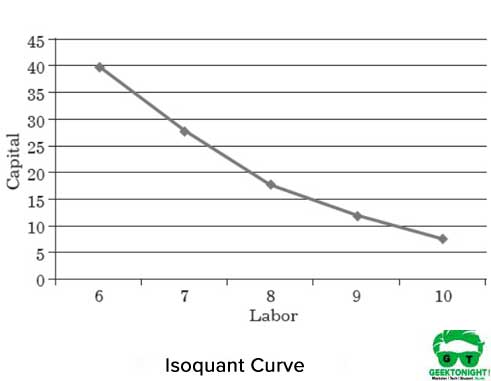
eigenschappen van de Isoquantkromme
enkele eigenschappen van de isoquantkromme zijn als volgt:
- Isoquant bochten helling naar beneden
- Isoquant curves zijn convex naar de oorsprong
- Isoquant bochten niet kruisen elkaar
- Hoger de isoquant hoe hoger de output

Isoquant bochten helling naar beneden
Het betekent dat de helling van de isoquant curve is negatief. Dit komt omdat wanneer kapitaal (K) wordt verhoogd, de hoeveelheid arbeid (L) wordt verminderd of omgekeerd, om hetzelfde productieniveau te behouden.
Isoquantkrommen zijn convex tot oorsprong
dit betekent dat factorinputs geen perfecte substituten zijn. Deze eigenschap toont de substitutie van inputs en de afnemende marginale mate van technische substitutie van isoquant. De marginale betekenis van een input (kapitaal) in termen van een andere input (arbeid) vermindert samen met de isoquant curve.
Figuur 2 toont de convexe isoquantcurve:
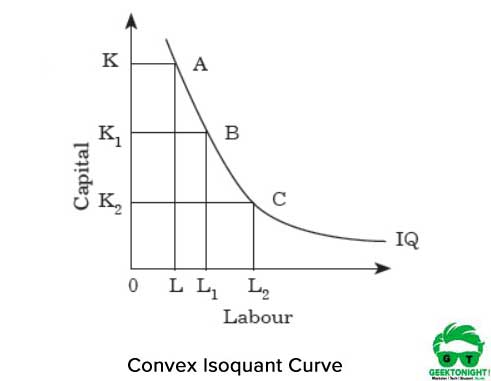
de convexiteit geeft aan dat de MRT ‘ s afnemen als we van punt A naar B en van B naar C langs de isoquant gaan. De MRT ‘ s verminderen omdat de twee inputs arbeid en kapitaal geen perfecte substituten zijn.
voor elke toename van de arbeid is er dus een daling van het kapitaal. Als de isoquant hol is, neemt de MRT ‘ s van arbeid voor kapitaal toe. Figuur 3 toont de concave isoquantcurve:
zoals weergegeven in Figuur 3, als we van punt A naar B en van B naar C langs de isoquant bewegen, neemt het MRT toe. Het toont aan dat de twee inputs arbeid en kapitaal perfecte substituten zijn. Voor elke toename van de arbeid is er dus een toename van het kapitaal.
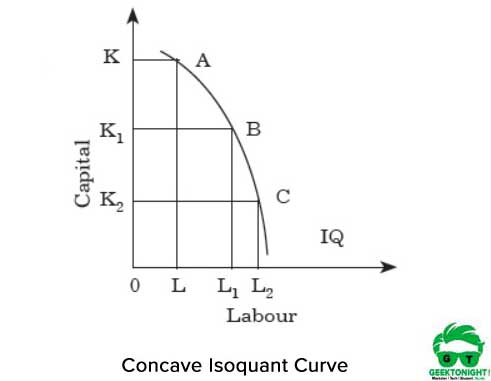
Isoquantkrommen kunnen elkaar niet snijden
een isoquant impliceert de verschillende niveaus van combinatie die verschillende niveaus van inputs produceren. Als de isoquanten elkaar snijden, betekent dit dat een enkele invoercombinatie twee uitvoerniveaus kan produceren, wat niet mogelijk is. De wet van de productie zou niet van toepassing zijn.
hoger de isoquant hoe hoger de output
het impliceert dat de hogere isoquant een hogere output vertegenwoordigt. De bovenste curve van de isoquant produceert meer output dan de curve eronder. Dit komt omdat de grotere combinatie van input resulteert in een grotere output in vergelijking met de curve die eronder is.
marginale technische Substitutiesnelheid
de helling van de isoquantcurve is de substitutiesnelheid die laat zien hoe een input kan worden vervangen door een andere terwijl de output constant wordt gehouden. Dit wordt marginal rate of technical substitution (MRTS) genoemd.
volgens Lipsey, ” kan de marginale technische substitutiesnelheid worden gedefinieerd als de snelheid waarbij een factor wordt vervangen door een andere, waarbij de output constant wordt gehouden.”
de formule voor het berekenen van MRTS is als volgt:
MRTS = – ∆K/∆L
waarbij ∆K = verandering in kapitaal
∆l= verandering in arbeid
de formule laat zien dat op een bepaald niveau van productie, MRTS van kapitaal voor arbeid de hoeveelheid arbeid zou impliceren die het bedrijf bereid zou zijn op te geven voor een extra kapitaaleenheid. Evenzo zou het MRT ‘ s van arbeid voor kapitaal de hoeveelheid kapitaal impliceren die de onderneming bereid zou zijn op te geven voor een extra eenheid arbeid.
MRTS is ook gelijk aan de verhouding tussen het marginale product van een input en het marginale product van een andere input. De output langs de isoquant is constant. Als de verandering in de Arbeid de verandering in het kapitaal vervangt, dan moet de toename van de productie als gevolg van de toename van de arbeid overeenkomen met de afname van de productie als gevolg van de afname van het kapitaal. Mathematisch
∆l X MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
aangezien de uitvoer onveranderd blijft bij een gegeven isoquant,
∆l X MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL) / MPK)
zo kunnen we zeggen dat mrt ‘ s tussen inputs gelijk zijn aan marginale producten van de inputs.
De MRTS is berekend zoals weergegeven in Tabel 2
| Arbeid | Hoofdstad | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
types of Isoquant Curve
er is een continue substitutie van een inputvariabele door de andere inputvariabele met een afnemend tempo. Perfecte aanvullingen en perfecte vervangers geven verschillende vormen van isoquanten.
de verschillende typen isoquantcurve zijn als volgt:
- Lineaire isoquant
- L-vormige isoquant

Lineaire isoquant
Het is een rechte lijn isoquant en staat voor een perfecte substitueerbaarheid tussen de ingangen, kapitaal en arbeid van de productiefunctie. Mrt ‘ s tussen ingangen blijven constant. Figuur 4 toont een lineaire isoquant:
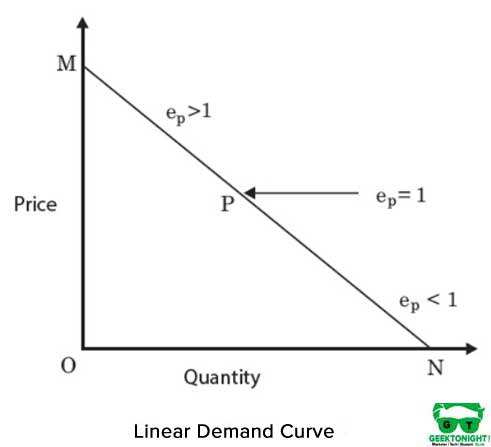
De algebraïsche vorm van de productiefunctie in het geval van lineaire isoquant is als volgt:
Q = aK + BL
Hier, Q is de gewogen som van K en L. De helling van de curve kan worden berekend met behulp van de volgende formule:
MPK = ∆Q/∆K = a
MPL = ∆Q/∆L = b
MRTS = MPL / MPK
MRTS = -b/a b/a is een constante)
Echter, lineaire isoquant niet hebben bestaan in de echte wereld.
L-vormige isoquant
dit is het geval van perfecte complementen. Daarbij is de combinatie van kapitaal en arbeid in een vaste verhouding. Slechts één combinatie van Arbeid en kapitaal is mogelijk om een product te produceren met een vast percentage van de inputs.
om de productie te verhogen, moet een organisatie beide inputs proportioneel verhogen. De grafische weergave van de vaste factor verhouding isoquant is L in vorm, weergegeven in Figuur 5:
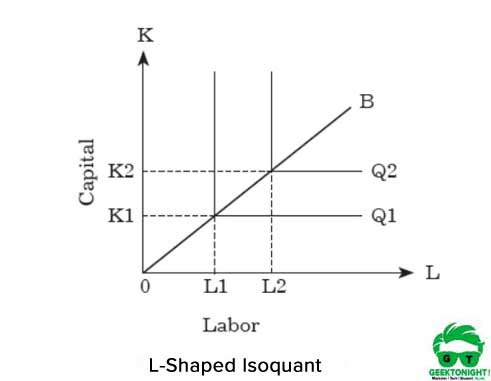
zoals blijkt uit Figuur 5, geeft de L-vormige isoquant aan dat er geen substitutie is tussen arbeid en kapitaal en wordt ervan uitgegaan dat zij complementaire goederen zijn. Men kan zien dat OK1-eenheden kapitaal en OL1-eenheden arbeid nodig zijn voor de productie van Q1.
om de productie van Q1 naar Q2 te verhogen, moet een organisatie de inputs verhogen van K1 naar K2 en L1 naar L2 beide. Deze verhouding tussen kapitaal en arbeid kan als volgt worden uitgedrukt::
Q = f (K, L) = min (aK, bL)
waarbij min betekent dat Q gelijk is aan lager van de twee termen, aK en bL
bijvoorbeeld, in geval AK > bL, Dan Q = bL en in geval AK < bL Dan Q = aK.
deze isoquant is dezelfde als de leontif-productiefunctie.
Substitutieelasticiteit tussen factoren
we weten dat MRTS de helling van de isoquant is. Het toont echter niet aan in welke mate de ene factor substitueerbaar is. Het is belangrijk om de mate van substitueerbaarheid tussen de twee inputs te meten.Daarom hebben economen een formule ontwikkeld voor het schatten van de mate van substitueerbaarheid tussen de twee inputs, kapitaal en arbeid, die bekend staat als elasticiteit van factorsubstitutie.
elasticiteit van factorsubstitutie (σ) verwijst naar de verhouding tussen de procentuele verandering in de verhouding kapitaal / arbeid en de procentuele verandering in mrt ‘ s.
het wordt wiskundig weergegeven als volgt:
σ = procentuele verandering in de verhouding kapitaal / arbeid/procentuele verandering in mrt ‘s
of,
σ = *
als ∆K/∆L = ∆mrt’ s ; σ = 1
If ∆K / ∆L > ∆MRTS; σ > 1
If ∆K / ∆L < ∆MRTS ; σ < 1
hoge elasticiteit van substitutie tussen factoren impliceert dat de factoren gemakkelijk onderling kunnen worden vervangen, terwijl een lage elasticiteit betekent dat substitutie van factoren tot op zekere hoogte mogelijk is.
in het geval van lineaire isoquant zou de substitutieelasticiteit oneindig zijn, en in het geval van L-vormige isoquanten zou deze nul zijn.
ISO-kostencurve
Iso-kostencurve is de locus van punten van alle verschillende combinaties van Arbeid en kapitaal die een organisatie kan gebruiken, gezien de prijs van deze inputs. Iso-kostenlijn vertegenwoordigt de prijs van factoren samen met de hoeveelheid geld die een organisatie bereid is te besteden aan factoren.
met andere woorden, het toont verschillende combinaties van factoren die tegen een bepaald bedrag kunnen worden gekocht. De helling van de iso-kostenlijn hangt af van de verhouding tussen de prijs van Arbeid en de prijs van kapitaal.
bijvoorbeeld, een producent heeft een totaal budget van ₹120, dat hij wil uitgeven aan de productiefactoren, namelijk X en Y. De prijs van X op de markt is ₹15 per eenheid en de prijs van Y is ₹10 per eenheid. Tabel 7.5 toont de combinaties:
| Combinaties | Eenheden van X | Eenheden van Y | Totaal uitgaven |
|---|---|---|---|
| Een | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
De iso-kosten regel is weergegeven in Figuur 7.8:
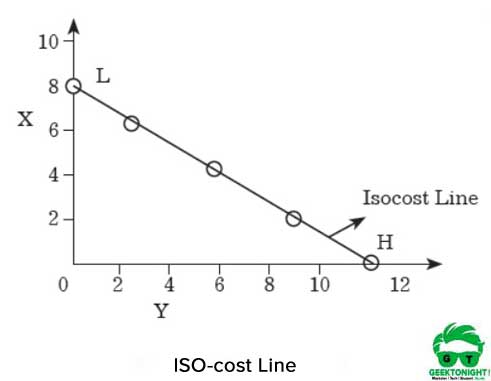
zoals blijkt uit Figuur 6, als de producent het hele bedrag uitgeeft om X te kopen, dan kan hij/zij 8 eenheden X kopen.aan de andere kant, als de producent Y koopt met het hele bedrag, dan zou hij/zij in staat zijn om 12 eenheden te krijgen.
als de punten H en L worden samengevoegd op respectievelijk de x-en de Y-as, dan wordt een rechte lijn verkregen, die iso-kostenlijn wordt genoemd. Alle combinaties van X en Y die op deze lijn liggen, zouden dezelfde kosten hebben die gelijk zijn aan ₹120.
ook andere ISO-kostenlijnen kunnen worden uitgezet door de kosten meer dan 120 te nemen, in het geval dat de producent bereid is om meer geld uit te geven aan de productiefactoren.
met behulp van isoquant-en iso-kostenlijnen kan een producent het punt bepalen waarop inputs maximale winst opleveren door minimale kosten te maken. Zo ‘ n punt wordt het evenwicht van de producent genoemd.
Ook Lezen: Hoofd-en ordinaal hulpprogramma
Bedrijfseconomie Tutorial
(klik op het onderwerp om te lezen)
Ga door, Deel artikel met vrienden
Leave a Reply