Krzywa izoquant: definicja, właściwości, typy, założenia
Co To jest krzywa Isoquant?
Krzywa Izoquant: zależność techniczna, która pokazuje, jak dane wejściowe są przekształcane w dane wyjściowe, jest przedstawiona za pomocą krzywej izoquant. Pokazuje on optymalne kombinacje czynników produkcji za pomocą cen czynników produkcji i ich ilości, które są wykorzystywane do produkcji tej samej produkcji.
termin ISO oznacza równe, a quant oznacza ilość lub wyjście.
na przykład do produkcji 100 kalendarzy wykorzystuje się 90 jednostek kapitału i 10 jednostek pracy.
krzywe Izoakustyczne nazywane są również jako krzywe równe produktowi lub krzywe obojętności produkcyjnej.
definicja krzywej Izoquant
założenia krzywej Izoquant
założenia krzywej izoquant są następujące:
- istnieją tylko dwa czynniki, praca i kapitał, aby wytworzyć konkretny produkt.
- kapitał, praca i dobra są podzielne z natury.
- kapitał i siła robocza są w stanie zastąpić się do pewnego limitu.
- technologia produkcji jest podawana w pewnym okresie czasu.
- czynniki produkcji są używane z pełną wydajnością.
poznajmy isoquant z pomocą poniższej tabeli.
Tabela 1 przedstawia różne kombinacje dwóch czynników produkcji, a mianowicie siły roboczej i kapitału do produkcji 150 ton produkcji:
| praca | kapitał |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
Rysunek 1 przedstawia krzywą izoquant różnych kombinacji kapitału pracowniczego, które pomagają w produkcji 150 ton produkcji:
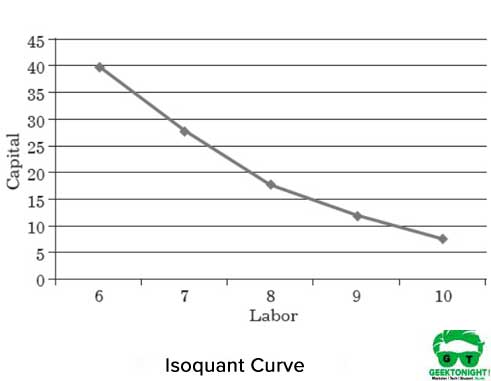
właściwości krzywej Izoquanta
niektóre właściwości krzywej izoquanta są następujące:
- krzywe Izoquanta nachylenie w dół
- krzywe Izoquanta są wypukłe do początku
- krzywe Izoquanta nie mogą się przecinać
- im wyższy izoquant tym wyższy wynik

krzywe Izoquant nachylają się w dół
oznacza to, że nachylenie krzywej izoquant jest ujemne. Dzieje się tak dlatego, że gdy kapitał (K) jest zwiększany, ilość pracy (L) jest zmniejszana lub odwrotnie, aby utrzymać ten sam poziom produkcji.
krzywe Izoukładowe są wypukłe do początkowego
oznacza to, że wejściowe współczynniki nie są doskonałymi substytutami. Ta właściwość pokazuje substytucję nakładów i malejącą krańcową stopę technicznej substytucji izoquantu. Marginalne znaczenie jednego wkładu (kapitału) w kategoriach innego wkładu (pracy) maleje wraz z krzywą izoquant.
Rysunek 2 przedstawia wypukłą krzywą izoukładu:
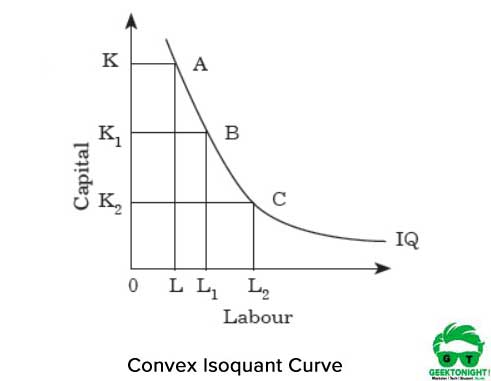
wypukłość oznacza, że MRT zmniejsza się, jeśli przejdziemy z punktu A do B i z B do C wzdłuż izoquanta. Wskaźniki MRT maleją, ponieważ oba czynniki Produkcji-Praca i kapitał-nie są doskonałymi substytutami.
Tak więc za każdy wzrost siły roboczej następuje spadek kapitału. Jeśli izoquant jest wklęsły, to MRT pracy na podwyższenie kapitału. Rysunek 3 przedstawia wklęsłą krzywą izochwantu:
jak pokazano na fig.3, jeśli przejdziemy z punktu A do B i z B do C wzdłuż izochwantu, MRT wzrośnie. Pokazuje to, że oba nakłady pracy i kapitału są doskonałymi substytutami. Tak więc, dla każdego wzrostu siły roboczej, jest wzrost kapitału.
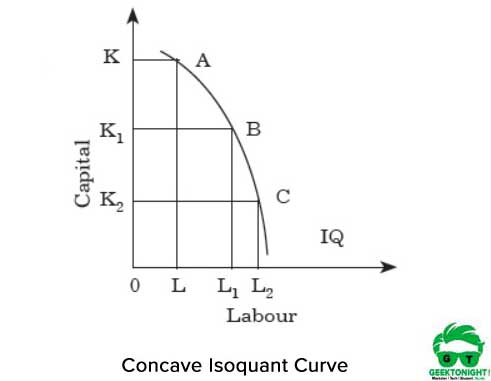
krzywe Izoquant nie mogą się przecinać
izoquant implikuje różne poziomy kombinacji wytwarzających różne poziomy wejść. Jeśli izoukanty przecinają się ze sobą, oznaczałoby to, że pojedyncza kombinacja wejściowa może wytworzyć dwa poziomy wyjściowe, co nie jest możliwe. Prawo produkcji nie miałoby zastosowania.
im wyższa wartość isoquant, tym wyższa wartość wyjściowa
, oznacza to, że im wyższa wartość isoquant, tym wyższa wartość wyjściowa. Górna krzywa izoquanta wytwarza więcej mocy niż krzywa poniżej. Dzieje się tak dlatego, że większa kombinacja danych wejściowych powoduje większą wydajność w porównaniu do krzywej znajdującej się pod nią.
krańcowa stopa podstawienia technicznego
nachylenie krzywej izoquant jest stopą podstawienia, która pokazuje, jak jedno wejście można zastąpić innym, utrzymując stałą wyjściową. Nazywa się to krańcową stopą technicznej substytucji (MRT).
według Lipseya ” krańcową stopę substytucji technicznej można zdefiniować jako szybkość, z jaką jeden czynnik jest zastępowany innym, a produkcja jest utrzymywana na stałym poziomie.”
wzór na obliczanie MRT jest następujący:
MRTS = – ∆K / ∆L
gdzie, ∆K = Zmiana kapitału
∆l= zmiana siły roboczej
wzór pokazuje, że przy danym poziomie produkcji, MRTS kapitału na pracę oznaczałoby ilość pracy, z której firma byłaby skłonna zrezygnować za dodatkową jednostkę kapitału. Podobnie, MRT pracy dla kapitału oznaczałoby ilość kapitału, którą firma byłaby skłonna poświęcić na dodatkową jednostkę pracy.
MRTS jest również równy stosunkowi produktu krańcowego z jednego wejścia do produktu krańcowego z innego wejścia. Wyjście wzdłuż izoquanta jest stałe. Jeżeli zmiana siły roboczej jest zastępowana zmianą kapitału, to wzrost produkcji spowodowany wzrostem siły roboczej powinien być zgodny ze spadkiem produkcji spowodowanym zmniejszeniem kapitału. Matematycznie
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
ponieważ wydajność pozostaje niezmieniona przy danym izoquancie,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
mrtskl = (mpl / MPK)
możemy więc powiedzieć, że MRT między wejściami jest równy marginalnym produktom wejść.
MRT oblicza się zgodnie z tabelą 2
| praca | kapitał | MRT |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
rodzaje krzywej Izoquant
istnieje ciągłe zastępowanie jednej zmiennej wejściowej przez drugą zmienną wejściową z malejącą szybkością. Doskonałe dopełnienia i doskonałe zamienniki dają różne formy izochwantów.
różne rodzaje krzywej izoquant są następujące:
- izochant liniowy
- izochant w kształcie litery L

izoquant liniowy
jest to izoquant liniowy i stanowi doskonałą substytucyjność między nakładami, kapitałem i pracą funkcji produkcyjnej. MRT między wejściami pozostaje stała. Rysunek 4 przedstawia liniowy izoquant:
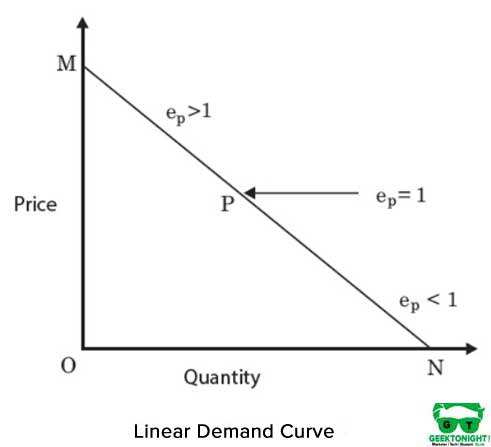
algebraiczna forma funkcji produkcyjnej w przypadku izoquanta liniowego jest następująca:
Q = aK + bl
tutaj Q jest sumą ważoną K I L. nachylenie krzywej można obliczyć za pomocą następującego wzoru:
MPK = ∆Q / ∆K = a
MPL = ∆Q/∆L = B
MRTS = MPL / MPK
MRTS = – b/A (B/A jest stała)
jednak izochant liniowy nie istnieje w świecie rzeczywistym.
L-shaped isoquant
jest to przypadek doskonałych uzupełnień. Zgodnie z tym połączenie kapitału i pracy jest w stałej proporcji. Tylko jedno połączenie siły roboczej i kapitału jest możliwe do wytworzenia produktu o ustalonej proporcji nakładów.
aby zwiększyć produkcję, organizacja musi proporcjonalnie zwiększyć oba nakłady. Graficzna reprezentacja proporcji czynnika stałego ma kształt L, pokazany na rysunku 5:
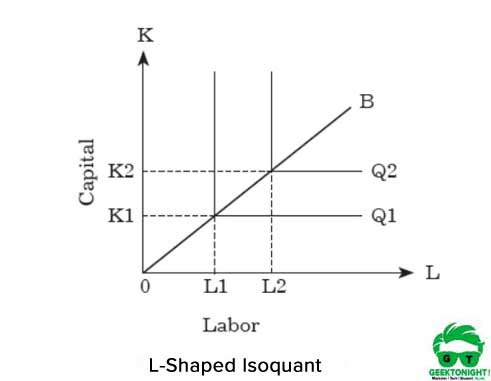
jak pokazano na rysunku 5, izoquant w kształcie litery L oznacza, że nie ma substytucji między pracą a kapitałem i zakłada się, że są to dobra komplementarne. Można zauważyć, że do produkcji Q1 potrzebne są jednostki kapitału OK1 i jednostki pracy OL1.
z drugiej strony, aby zwiększyć produkcję z Q1 do Q2, organizacja musi zwiększyć nakłady z K1 do K2 i L1 do L2. Związek między kapitałem a pracą można wyrazić następująco:
Q = f (K, L) = min(aK, bl)
gdzie, min oznacza q równe niższemu z dwóch wyrażeń, aK i bl
na przykład w przypadku aK > bl, wtedy Q = bl, a w przypadku aK < BL wtedy, Q = aK.
to jest to samo co funkcja produkcyjna leontif.
elastyczność substytucji między czynnikami
wiemy, że MRTS jest nachyleniem izoquantu. Nie ujawnia jednak stopnia substytucyjności jednego czynnika dla drugiego. Ważne jest, aby zmierzyć stopień zastępowalności między dwoma wejściami.
w związku z tym ekonomiści opracowali formułę szacowania zakresu substytucyjności między dwoma wkładami, kapitałem i pracą, znaną jako elastyczność substytucji czynnikowej.
elastyczność substytucji czynnika (σ) odnosi się do stosunku procentowej zmiany stosunku kapitału do pracy do procentowej zmiany MRT.
jest matematycznie reprezentowany w następujący sposób:
σ = procentowa zmiana wskaźnika pracy kapitału/procentowa zmiana MRT
lub,
σ = *
jeśli ∆K / ∆L = ∆MRTS ; σ = 1
jeśli ∆K/∆L > Mr MRTS ; σ >1
jeśli ∆K/∆L <Mr MRTS; σ < 1
Wysoka elastyczność substytucji między czynnikami oznacza, że czynniki mogą być łatwo podstawione do siebie, podczas gdy niska elastyczność oznacza, że substytucja czynników jest możliwa do pewnego stopnia.
w przypadku izochwanów liniowych elastyczność podstawienia byłaby nieskończona, a w przypadku izochwanów w kształcie litery L-zero.
krzywe kosztów ISO
Krzywa kosztów Iso jest miejscem punktów wszystkich różnych kombinacji pracy i kapitału, które organizacja może zatrudnić, biorąc pod uwagę cenę tych nakładów. Linia Iso – cost przedstawia cenę czynników wraz z kwotą pieniędzy, którą organizacja jest skłonna wydać na czynniki.
innymi słowy, pokazuje różne kombinacje czynników, które można kupić za określoną kwotę pieniędzy. Nachylenie linii iso-cost zależy od stosunku ceny Pracy Do ceny kapitału.
na przykład producent ma całkowity budżet ₹120, który chce wydać na czynniki produkcji, a mianowicie X i Y. Cena X na rynku wynosi ₹15 za jednostkę, a cena Y wynosi ₹10 za jednostkę. Tabela 7.5 przedstawia kombinacje:
| kombinacje | jednostki x | jednostki Y | wydatki ogółem |
|---|---|---|---|
| A | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
linia kosztu iso jest pokazana na rysunku 7.8:
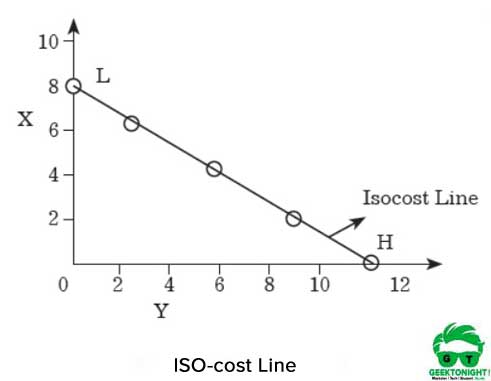
jak pokazano na rysunku 6, jeśli producent wyda całą kwotę pieniędzy na zakup X, to może kupić 8 jednostek X. Z drugiej strony, jeśli producent kupi Y z całą kwotą,wtedy będzie mógł uzyskać 12 jednostek.
jeśli punkty H I L są połączone odpowiednio na osiach X i Y, to otrzymuje się linię prostą, którą nazywa się linią iso-cost. Wszystkie kombinacje X i Y, które leżą na tej linii, będą miały tę samą kwotę kosztu, która wynosi ₹120.
podobnie, inne linie iso-cost mogą być wykreślone przez koszt ponad 120, W przypadku gdy producent jest skłonny wydać więcej pieniędzy na czynniki produkcyjne.
za pomocą linii isoquant i iso-cost producent może określić punkt, w którym nakłady przynoszą maksymalny zysk, ponosząc minimalny koszt. Taki punkt określany jest jako równowaga producenta.
Czytaj Także: Użyteczność kardynalna i porządkowa
poradnik Ekonomiki biznesu
(kliknij na temat, aby przeczytać)
dalej, podziel się artykułem ze znajomymi
Leave a Reply