Wzory matematyczne 31 aktu, które musisz znać

Geometria płaszczyzny

kąty i linie

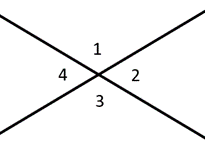
Kąty wzdłuż linii nazywane są kątami dodatkowymi, sumując się do \(180^{\circ}\). Kąty komplementarne sumują się do \(90^{\circ}\), kąta prostego. Kąty pionowe opisują kąty naprzeciwko siebie, które są zawsze przystające. Na przykład na diagramie po lewej stronie powiemy, że kąty 1 & 2 są dodatkowymi, podczas gdy kąty 1 & 3 są kątami pionowymi.

Powierzchnia trójkąta

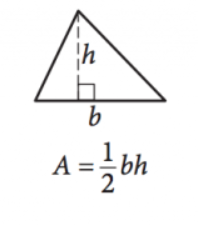
Zdjęcie dzięki uprzejmości SAT

\(\frac{1}{2}bh=a\)

to równanie przedstawia pole \((a)\) dowolnego trójkąta o długości podstawy \((b)\) i wysokości \((h)\). Zauważ, że wysokość jest długością linii rozciągającej się pod kątem dopełniającym od dowolnego boku (podstawy) do punktu/kąta bezpośrednio naprzeciwko tego boku.

dla trójkątów równobocznych, gdzie wszystkie trzy boki \((s)\) są tej samej długości, równanie pola wynosi:

\(\frac{s^2\sqrt{3}}{4} = A\)

Twierdzenie Pitagorasa

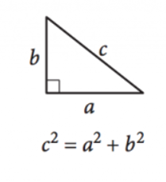
Zdjęcie dzięki uprzejmości SAT

ponieważ kąty w trójkącie zawsze sumują się do \(180^{\circ}\), trójkąt prostokątny jest zdefiniowany jako dowolny trójkąt o jednym kącie prostym, zapewniając, że pozostałe dwa kąty są komplementarne. Długości boku trójkątów prostokątnych można określić twierdzeniem Pitagorasa:

\(a^2+b^2=c^2\)

tutaj \(a\) i \(b\) są długościami nóg lub boków w poprzek kątów komplementarnych, A \(c\) jest długością przeciwprostokątnej, boku w poprzek kąta prostego.

pomocne może być również zapamiętanie następujących trójek pitagorejskich lub wartości długości boku \((a,b, c)\): 3-4-5, 5-12-13, 7-24-25, i 8-15-17. Zauważ, że przeciwprostokątna jest zawsze najdłuższym bokiem.

specjalne Trójkąty prostokątne

istnieją dwa rodzaje specjalnych trójkątów prostokątnych, które mają następujące współczynniki kątów i długości:

Zdjęcie dzięki uprzejmości SAT

obszary czworokątów

\(a = lw\)

ten wzór przedstawia powierzchnię prostokąta o długości \(l\) i szerokości \(w\).

\(a = bh\)

ten wzór podaje pole równoległoboku podanej podstawy \(b\) , Długość najdłuższych boków i wysokość \(h\), zdefiniowaną jako długość linii rozciągającej się pod komplementarnym kątem w górę od jednej podstawy do drugiej.

\(a= \ frac{b_1+b_2}{2}\: \ times\:H\)

ten wzór podaje pole trapezu o bazach \(b_1\) i \(b_2\) oraz wysokości \(h\), zdefiniowane w ten sam sposób jak dla równoległoboku.

kąty wewnętrzne wielokątów regularnych

\((n-2)\:\times\:180^{\circ}= s\)

w wielokącie regularnym, gdzie wszystkie boki i kąty są równe, wzór ten podaje sumę \(S)\) kątów wewnętrznych danego wielokąta O \(N\) bokach i kątach. Możemy również znaleźć każdy kąt wewnętrzny, obliczając \(\frac{S}{n}\).

Długość łuku w Kole

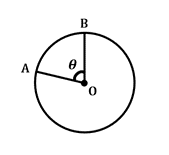
\(\frac {\theta} {360^{\circ}}\: \ times\:2\pi r=arc\: length\)

ten wzór określa długość łuku lub odcinka obwodu okręgu, pomiędzy dwoma określonymi promieniami przecinającymi się w środku okręgu z kątem centralnym \(\theta\). Zauważ, że \(2 \ pi r\) uwzględnia Obwód okręgu w tym wzorze.

obszar sektora w okręgu

\(\frac{\theta}{360^{\circ}}\:\times\:\pi R^2 = Sektor\:obszar\)

podobnie jak długość łuku, ten wzór zapewnia obszar sektora między dwoma określonymi promieniami przecinającymi się w środku okręgu z kątem centralnym . \ (\Pi R^2\) uwzględnia obszar okręgu w tym wzorze.

Kształty 3D

\(SA = 2 (lw + wh + lh)\)

\(V = lwh\)

te wzory zapewniają pole powierzchni \((SA)\) i objętość \((V)\) dla prostokątnego pryzmatu o długości \(l\), szerokości \(w\) i wysokości \(h\).

\(V=\pi r^2h\)

jest to wzór objętości dla prawego cylindra o promieniu podstawy \(r\) i wysokości \(h\).

jeśli potrzebujesz formuły powierzchni lub objętości dla innych kształtów 3D, ustawa zapewni odpowiednie formuły w samych pytaniach.

Trygonometria

SOH-CAH-TOA

większość problemów trygonometrii aktu polega na manipulowaniu sinusem, cosinusem i styczną, które są obliczane w następujący sposób dla danego kąta \(x\) w trójkącie prostokątnym:

\(sin(x)= \ frac{opposite\: leg}{przeciwprostokątna}\)

\(cos (x)=\frac{adjactive\: leg}{przeciwprostokątna}\)

\(tan (x)= \ frac{opposite\: leg}{adjactive\: leg} = \frac{sin (x)} {cos(x)}\)

SOH-CAH-TOA jest łatwym mnemonikiem do zapamiętywania, która funkcja trygonometryczna odpowiada której długości boków!

\(sin(x) = cos (90^{\circ} – x)\)

\(cos (x) = sin(90^{\circ}-x)\)

w słowach, te tożsamości pokazują, że funkcja trygonometryczna kąta \(x\) jest równa wartości współfunkcji dopełniacza \(x\). Są one powszechnie stosowane w przypadku bardziej zaawansowanej trygonometrii, pozwalając na łatwe konwersje między sinusem i cosinusem.

stosunek / wzajemne tożsamości trygonometryczne

czasami można zobaczyć wzajemne tożsamości \(sin (x)\),\ (cos (x)\) I \(tan (x)\), które są:

\(csc (x) =\frac{1}{sin (x)}\)

\(sec (x) = \ frac{1}{cos(x)}\)

\(cot (x) =\frac{1}{tan (x)}\)

tożsamość Pitagorejska

\(sin^2(x)+cos^2 (x)=1\)

na podstawie twierdzenia Pitagorasa i koła jednostkowego, tożsamość ta jest zwykle używana wraz z tożsamościami współfunkcji do rozwiązywania problemów trygonometrycznych (Kalkulator sans), gdzie kąt \(x\) lub wartości tych funkcji trygonometrycznych \(x\) są nieznane.

Statystyka i prawdopodobieństwo

procenty

\(n\%\: of\: m = \ frac{n}{100}\: \ times\:m\)

procenty są używane do wyrażania części całości, a symbol \(\%\) ogólnie oznacza ” podziel przez 100.”Jako takie, powyższe równanie odpowiada na każdy problem z pytaniem o \(n\%\) ilości \(m\).

średnia, mediana, tryb i zakres

ustawa sprawdza podstawową wiedzę statystyczną, z reguły obejmującą poniższe środki:

• Średnia to średnia, czyli \(\frac{sum\:of\:all\:terms}{total\:number\: of\:warunki}\)
• Mediana to środkowy termin, lub średnia z dwóch środkowych terminów, jeśli istnieje parzysta liczba terminów
• tryb to termin(Y), który występuje najczęściej
• zakres jest różnicą między największym i najmniejszym terminem

prawdopodobieństwo

\(P(A) = \frac{Numer\:of\:desired\:outcomes}{total\:number\:of\:possible\:outcomes}\)

prawdopodobieństwo reprezentuje prawdopodobieństwo wystąpienia zdarzenia \((a)\), obliczone przez podzielenie liczby pożądanych wyników przez liczbę całkowitych możliwych wyników. Na przykład prawdopodobieństwo wyrzucenia 6 na parzystej kości wynosi \(\frac{1}{6}\).

Niezależne zdarzenia

\(P(A\:and\:b) = P(a)\:\times\:P(B)\)

zdarzenia \(a\) i \(B\) są niezależne, Jeśli \(a\) występujące nie wpływa na prawdopodobieństwo wystąpienia \(B\). Aby obliczyć prawdopodobieństwo wystąpienia obu niezależnych zdarzeń, mnożymy ich indywidualne prawdopodobieństwa razem. Na przykład prawdopodobieństwo dwukrotnego odwrócenia reszek wynosi \(\frac{1}{2}\:\times\: \ frac{1} {2}=\frac{1} {4}\).

podsumowanie

w tym poście omówiliśmy wiele formuł, ale pamiętaj również o przejrzeniu wszystkich pojęć matematycznych poprzez algebrę II i geometrię! Na przykład, możesz oczekiwać, że liczby złożone, wektory, macierze, układy równań i manipulowanie funkcjami graficznymi również będą w teście. Zobacz pełny opis działu matematyka aktu, aby uzyskać więcej informacji.

pamiętaj, że praktyka czyni mistrza, szczególnie w matematyce! Będziesz chciał wypróbować wiele różnych problemów przed dniem testowym, aby naprawdę zrozumieć, jak zastosować i zintegrować te pojęcia i formuły w odpowiednim czasie.

skoro masz prawo do kalkulatora aktu, radzimy go zabrać, ale ze słowem ostrożności. Pamiętaj, że każdy problem matematyczny można rozwiązać bez kalkulatora i łatwo jest marnować cenny czas za pomocą kalkulatora, gdy faktycznie nie musisz. W związku z tym wykonaj sekcje ćwiczeń z czasem za pomocą kalkulatora, jeśli planujesz je przynieść, i pamiętaj, że jest to tylko ostateczność: aby ułatwić obliczenia i zwiększyć prędkość. Sięgaj po niego rzadko i sprawdź, czy twój konkretny model jest dozwolony zgodnie z Polityką kalkulatora ACT.