31 LEI de Fórmulas Matemáticas que Você Precisa Saber

Geometria plana

Ângulos e Linhas

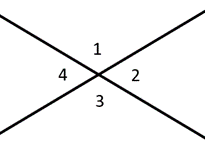
Ângulos ao longo de uma linha são chamados de ângulos suplementares, adicionando-se a \(180^{\circ}\). Ângulos complementares somam \(90^{\circ}\), um ângulo reto. Ângulos verticais descrevem ângulos diretamente um do outro, que são sempre congruentes. No diagrama à esquerda, por exemplo, diríamos que os ângulos 1 & 2 são suplementares, enquanto os ângulos 1 & 3 são ângulos verticais.

Área de um Triângulo

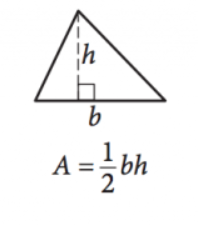
Imagem cortesia de SAT

\(\frac{1}{2}bh=A\)

Esta equação fornece a área em \((A)\) de qualquer triângulo dado comprimentos da base \((b)\) e a altura \((h)\). Observe que a altura é o comprimento da linha que se estende em um ângulo complementar de qualquer lado (a base) até o ponto/ângulo diretamente em frente a esse lado.

para triângulos equiláteros, onde todos os três lados\ ((s)\) têm o mesmo comprimento, a equação da área é:

\(\frac{s^2\sqrt{3}}{4}=A\)

o Teorema de Pitágoras

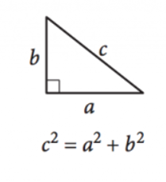
Imagem cortesia de SAT

Como ângulos de um triângulo sempre somam para \(180^{\circ}\), um triângulo é definido como qualquer triângulo com um ângulo direito, garantir os outros dois ângulos são complementares. Os comprimentos laterais dos triângulos retângulos podem ser definidos pelo teorema de Pitágoras:

\(a^2+b^2=c^2\)

Aqui, \(a\) e \(b\) são os comprimentos das pernas ou os lados através de ângulos complementares, e \(c\) é o comprimento da hipotenusa, o lado de frente para o ângulo direito.

pode ser útil também memorizar os seguintes triplos Pitagóricos, ou valores para o lado comprimentos \((a,b,c)\): 3-4-5, 5-12-13, 7-24-25, e 8-15-17. Observe que a hipotenusa é sempre o lado mais longo.

triângulos retângulos especiais

existem dois tipos de triângulos retângulos especiais, que têm os ângulos e as proporções de comprimento da seguinte forma:

Imagem cortesia de SAT

Áreas de Quadriláteros

\(A = lw\)

Esta fórmula fornece a área de um retângulo com o comprimento de \(l\) e largura \(l\).

\(A = bh\)

Esta fórmula fornece a área de um paralelogramo de base \(b\) , o comprimento dos lados maiores, e a altura de \(h\), definido como o comprimento da linha estendendo-se em um ângulo complementar para cima a partir de uma base para a outra.

\(a=\frac{b_1+b_2}{2}\:\times\:h\)

esta fórmula fornece a área de um trapézio com bases \(b_1\) e \(b_2\) e altura \(h\), definidas da mesma forma que para paralelogramas.

Interior de Ângulos de Polígonos Regulares

\((n-2)\:\times\:180^{\circ}= S\)

Em um polígono regular, onde todos os lados e ângulos são iguais, esta fórmula fornece a soma \((S)\) dos ângulos interiores dado um polígono com \(n\) os lados e ângulos. Também podemos encontrar cada ângulo interior calculando \(\frac {s} {n}\).

Comprimento do Arco de um Círculo

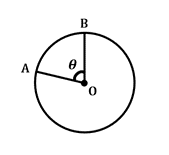
\(\frac{\theta}{360^{\circ}}\:\vezes\:2\pi r=arc\:comprimento\)

Esta fórmula define o comprimento do arco, ou a seção do círculo, circunferência, entre dois raios de interseção no centro do círculo com ângulo central \(\theta\). Observe que o\ (2 \ pi r\) incorpora a circunferência do círculo nesta fórmula.

Sector da Área de um Círculo

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = sector\:área\)

Semelhante ao comprimento de arco, esta fórmula fornece a área do setor, entre dois raios de interseção no centro do círculo com ângulo central . O\ (\pi r^2\) incorpora a área do círculo nesta fórmula.

Formas 3D

\(SA = 2(lw + wh + lh)\)

\(V= cla\)

Estas fórmulas fornecer a área de superfície \((SA)\) e o volume \((V)\) para um prisma retangular com comprimento de \(l\), largura \(m\), e altura de \(h\).

\(V=\pi r^2h\)

esta é a fórmula de volume para um cilindro direito com raio de base \(r\) e altura \(h\).

se você precisar das fórmulas de área de superfície ou volume para quaisquer outras formas 3D, O ACT fornecerá fórmulas relevantes nas próprias perguntas.

Trigonometria

SOH-CAH-TOA

Mais AGIR trigonometria problemas envolvem a manipulação de seno, co-seno e tangente, que são calculados da seguinte forma para um dado ângulo de \(x\) em um triângulo:

\(sin(x)=\frac{oposto\:perna}{hipotenusa}\)

\(cos(x)=\frac{adjacentes\:perna}{hipotenusa}\)

\(tan(x)=\frac{oposto\:perna}{adjacentes\:perna}=\frac{sin(x)}{cos(x)}\)

SOH-CAH-TOA é um fácil mnemônico para lembrar que trigonométricas função corresponde à função de que lado comprimentos!

Cofunction Identidades

\(sin(x) = cos(90^{\circ}-x)\)

\(cos(x) = sin(90^{\circ}-x)\)

Em palavras, essas identidades mostrar que uma função trigonométrica do ângulo de \(x\) é igual ao valor da cofunction do complemento de \(x\). Eles são geralmente usados ao lidar com trigonometria mais avançada, permitindo conversões fáceis entre seno e cosseno.

Ratio/Reciprocal Trig Identities

você pode ocasionalmente ver as identidades recíprocas de \(sin (x)\), \(cos (x)\) e \(tan (x)\), que são:

\(csc(x) =\frac{1}{sin(x)}\)

\(sec(x) =\frac{1}{cos(x)}\)

\(berço(x) =\frac{1}{tan(x)}\)

Pitágoras de Identidade

\(sin^2(x)+cos^2(x)=1\)

com Base no Teorema de Pitágoras e o círculo da unidade, esta identidade é geralmente utilizado juntamente com o cofunction identidades para resolver problemas de trigonometria sans (calculadora) onde o ângulo \(x\) ou os valores das funções trigonométricas de \(x\) são desconhecidos.

Estatísticas e Probabilidade

Percentagens

\(n\% \:de\:m = \frac{n}{100}\:\vezes\:m\)

porcentagens são usadas para expressar partes de um todo, e o símbolo \(\%\) geralmente significa “dividir por 100.”Como tal, a equação acima responde a qualquer problema pedindo \(n\%\) de quantidade \(m\).

Média, Mediana, modo e intervalo

o ACT testa conhecimentos estatísticos básicos, geralmente envolvendo as medidas abaixo:

• a média é a média, ou \(\frac{soma\: de\: todos\: Termos} {total\: número\: de\:termos}\)
• Mediana é o meio termo, ou a média dos dois meio termos, se houver um número par de termos

Modo-é o termo(s) que ocorre com mais freqüência

• Intervalo é a diferença entre o maior e o menor dos termos

Probabilidade

\(P(A) = \frac{número\:de\desejado\:resultados}{total\:número\:de\possíveis:\: resultados}\)

a Probabilidade representa a probabilidade de um evento \((A)\) ocorrendo, calculado dividindo-se o número de resultados desejados pelo número total de resultados possíveis. Por exemplo, a probabilidade de rolar um 6 em um dado par é \(\frac{1}{6}\).

Eventos Independentes

\(P(A\:e\B) = P(A)\:\times\:P(B)\)

Eventos de \(A\) e \(B\) são independentes se \(A\) ocorrência de não afetar a probabilidade de \(B\) ocorrendo. Para calcular a probabilidade de que ambos os eventos independentes ocorram, multiplicamos suas probabilidades individuais juntos. Por exemplo, a probabilidade de virar cabeças duas vezes é \(\frac{1} {2}\:\times\:\frac{1} {2}=\frac{1} {4}\).

encerrando

cobrimos muitas fórmulas neste post, mas não deixe de revisar todos os conceitos matemáticos por meio de Álgebra II e geometria! Por exemplo, você pode esperar que números complexos, vetores, matrizes, sistemas de equações e manipulação de funções gráficas também estejam no teste. Veja Esta descrição completa da seção ACT math para mais informações.

lembre-se que a prática faz perfeito, especialmente para a matemática! Você vai querer experimentar muitos problemas diferentes antes do dia do teste, com o objetivo de realmente entender como aplicar e integrar esses conceitos e fórmulas em tempo hábil.

como você tem permissão para uma calculadora para o ato, aconselhamos trazer um, mas com uma palavra de cautela. Lembre-se que cada problema de Matemática ACT pode ser resolvido sem uma calculadora, e é fácil perder tempo valioso usando sua calculadora quando você realmente não precisa. Como tal, faça seções de prática cronometradas com sua calculadora se você planeja trazer uma e lembre-se de que ela só está lá como último recurso: para facilitar os cálculos e aumentar sua velocidade. Alcance-o raramente e verifique se seu modelo específico é permitido de acordo com a política da calculadora ACT.