Curva isoquante: definição, propriedades, tipos, suposições
o que é a curva Isoquant?
curva Isoquant: uma relação técnica que mostra como as entradas são convertidas em saída é representada por uma curva isoquant. Ele mostra as combinações ideais de insumos fatoriais com a ajuda de preços de insumos fatoriais e suas quantidades que são usadas para produzir a mesma saída.
o termo ISO implica igual e quant significa quantidade ou saída.
por exemplo, para produzir 100 calendários, são utilizadas 90 unidades de capital e 10 unidades de trabalho.
as curvas Isoquantes também são chamadas de curvas de produto iguais ou curvas de indiferença de produção.
definição da curva Isoquante
suposições da curva Isoquante
as suposições de uma curva isoquante são as seguintes:
- existem apenas dois fatores, trabalho e capital, para produzir um determinado produto.Capital, trabalho e bens são divisíveis por natureza.
- Capital e trabalho são capazes de substituir uns aos outros até um certo limite.
- a tecnologia de produção é fornecida ao longo de um período de tempo.
- fatores de produção são usados com eficiência total.
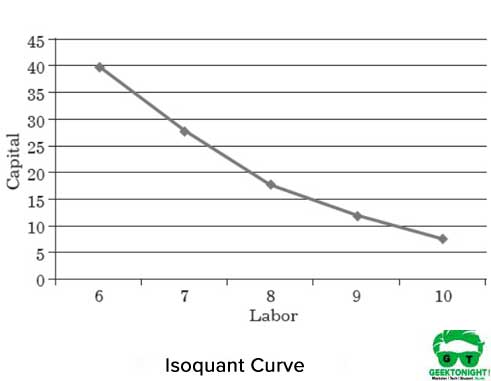
vamos aprender isoquant com a ajuda da tabela a seguir.
Tabela 1 mostra as diferentes combinações de dois fatores de inputs, ou seja, o trabalho e o capital para a produção de 150 toneladas de saída:
| de Trabalho | Capital |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
a Figura 1 mostra a isoquant curva de diferentes trabalho, o capital combinações que ajuda na produção de 150 toneladas de saída:
Propriedades de Isoquant Curva
Algumas das propriedades do isoquant curva são como segue:
- Isoquant curvas de inclinação para baixo
- Isoquant curvas são convexos a origem
- Isoquant curvas não se interceptam
- Maior o isoquant o maior saída

Isoquant curvas de inclinação para baixo
Isso implica que o declive da isoquant curva é negativa. Isso ocorre porque quando o capital (K) é aumentado, a quantidade de trabalho (L) é reduzida ou vice-versa, para manter o mesmo nível de produção.
as curvas Isoquentes são convexas à origem
isso implica que as entradas dos fatores não são substitutos perfeitos. Esta propriedade mostra a substituição de insumos e a diminuição da taxa marginal de substituição técnica do isoquante. A significância marginal de uma entrada (capital) em termos de outra entrada (trabalho) diminui junto com a curva isoquante.
a Figura 2 mostra a curva isoquante convexa:
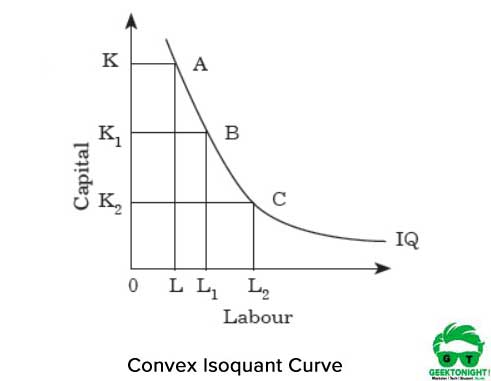
a convexidade representa que os MRTS diminuem se passarmos do ponto a para B e de B para C ao longo do isoquante. Os MRTS diminuem porque os dois insumos trabalho e capital não são substitutos perfeitos.
assim, para cada aumento do trabalho, há uma diminuição do capital. Se isoquant é côncavo, os MRTS de trabalho para o capital aumentam. A figura 3 mostra a curva isoquante côncava:
conforme mostrado na Figura 3, se nos movermos do ponto a para B e de B para C ao longo do isoquante, os MRTS aumentam. Mostra que os dois insumos trabalho e capital são substitutos perfeitos. Assim, para cada aumento de trabalho, há um aumento de capital.
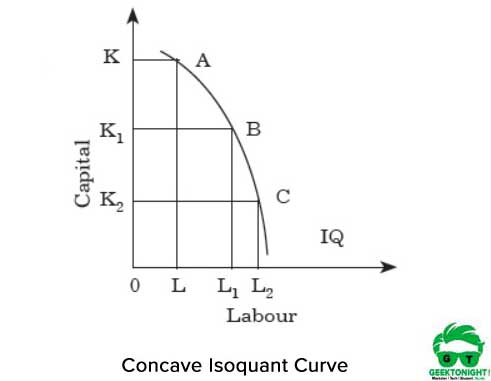
Isoquant curvas não se interceptam
Um isoquant implica diferentes níveis de combinação, produzindo diferentes níveis de inputs. Se os isoquantes se cruzarem, isso implicaria que uma única combinação de entrada pode produzir dois níveis de saída, o que não é possível. A lei da produção não seria aplicável.
quanto maior o isoquante, maior a saída
isso implica que o isoquante maior representa uma saída maior. A curva superior do isoquante produz mais saída do que a curva abaixo. Isso ocorre porque a combinação maior de entrada resulta em uma saída maior em comparação com a curva que está abaixo dela.
taxa Marginal de substituição técnica
a inclinação da curva isoquante é a taxa de substituição que mostra como uma entrada pode ser substituída por outra enquanto mantém a constante de saída. Isso é chamado de taxa marginal de substituição técnica (MRTS).
de acordo com Lipsey, ” a taxa marginal de substituição técnica pode ser definida como a taxa na qual um fator é substituído por outro com saída mantida constante.”
a fórmula para calcular MRTS é a seguinte:
MRTS = – ∆K/∆L
onde, ∆K = Mudança de capital
∆L= Mudança de trabalho
A fórmula mostra que, a um dado nível de produção, MRTS de capital para o trabalho, implica o tempo de trabalho de que a empresa estaria disposta a desistir de uma unidade adicional de capital. Da mesma forma, MRTS de trabalho para o capital implicaria a quantidade de capital que a empresa estaria disposta a desistir por uma unidade adicional de trabalho.
MRTS também é igual à razão entre o produto marginal de uma entrada e o produto marginal de outra entrada. A saída ao longo do isoquante é constante. Se a mudança no trabalho for substituída pela mudança no capital, o aumento da produção devido ao aumento do trabalho deve corresponder à diminuição da produção devido à diminuição do capital. Matematicamente
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Desde a saída permanece inalterada, em um determinado isoquant,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
Assim, podemos dizer que MRTS entre entradas é igual para produtos marginais dos insumos.
A MRTS é calculado como mostrado na Tabela 2
| de Trabalho | Capital | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
tipos de curva Isoquante
há uma substituição contínua de uma variável de entrada pela outra variável de entrada a uma taxa decrescente. Complementos perfeitos e substitutos perfeitos dão diferentes formas de isoquantes.
os diferentes tipos de curva isoquante são os seguintes:
- Linear isoquant
- em forma de L isoquant

Linear isoquant
é uma linha reta isoquant e representa uma substitutibilidade perfeita entre os insumos, capital e trabalho, de função de produção. MRTS entre entradas permanece constante. A figura 4 mostra um isoquante linear:
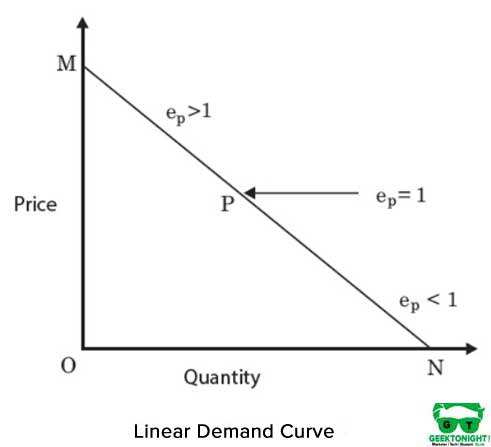
A forma algébrica da função de produção, no caso de linear isoquant é como segue:
Q = aK + BL
Aqui, Q é a soma ponderada de K e L. A inclinação da curva pode ser calculada com a ajuda da seguinte fórmula:
MPK = ∆Q/∆K = a
MPL = ∆Q/∆L = b
MRTS = MPL / MPK
MRTS = -b/a b/a é constante)
no Entanto, linear isoquant não têm existência no mundo real.
isoquant em forma de L
este é o caso de complementos perfeitos. Sob isso, a combinação entre capital e trabalho está em uma proporção fixa. Apenas uma combinação de trabalho e capital é possível produzir um produto com proporção afixada de insumos.
para aumentar a produção, uma organização precisa aumentar os dois insumos proporcionalmente. A representação gráfica do isoquante de proporção de fator fixo é L em forma, mostrada na Figura 5:
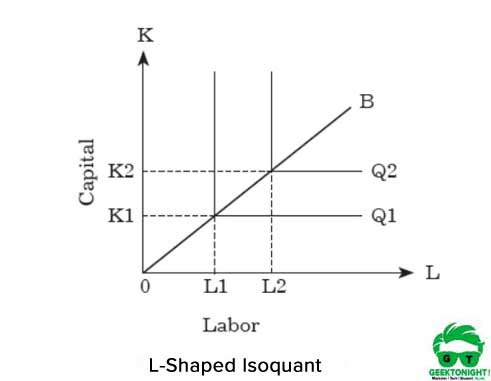
Como mostrado na Figura 5, a forma de L, isoquant representa que não há substituição entre trabalho e capital, e eles são considerados bens complementares. Pode-se ver que as unidades OK1 de capital e as unidades OL1 de trabalho são necessárias para a produção do primeiro trimestre.
por outro lado, para aumentar a produção de Q1 para Q2, uma organização precisa aumentar os insumos de K1 para K2 e L1 para L2 ambos. Essa relação entre capital e trabalho pode ser expressa da seguinte forma:
Q = f (K, L) = min (aK, bL)
onde, min implica Q é igual ao menor dos dois termos, aK e bL
Por exemplo, no caso de aK > bL, então Q = bL e, no caso de aK < bL então, Q = aK.
este isoquante é o mesmo que a função de produção leontif.
elasticidade de substituição entre fatores
sabemos que MRTS é a inclinação do isoquante. No entanto, não revela o grau de substituibilidade de um fator para outro. É importante medir o grau de substituibilidade entre as duas entradas.Portanto, os economistas desenvolveram uma fórmula para estimar a extensão da substituibilidade entre os dois insumos, capital e trabalho, que é conhecida como elasticidade da substituição de fatores.
elasticidade da substituição fatorial (σ) refere-se à razão entre variação percentual na relação capital-trabalho e a variação percentual nos MRTS.
é representado matematicamente da seguinte forma:
σ = mudança percentual no capital de trabalho taxa/porcentagem de alteração da MRTS
Ou,
σ = *
Se ∆K/∆L = ∆MRTS ; σ = 1
Se ∆K/∆L > ∆MRTS ; σ > 1
Se ∆K/∆L < ∆MRTS ; σ < 1
Alta elasticidade de substituição entre fatores implica que os fatores podem ser facilmente substituídos uns com os outros, enquanto uma baixa elasticidade representa a substituição de fatores, é possível até certo ponto.
no caso de isoquante linear, a elasticidade de substituição seria infinita e, no caso de isoquantes em forma de L, seria zero.
curvas de custo ISO
a curva de custo Iso é o locus de pontos de todas as diferentes combinações de trabalho e capital que uma organização pode empregar, dado o preço desses insumos. A linha Iso-cost representa o preço dos fatores, juntamente com a quantidade de dinheiro que uma organização está disposta a gastar em fatores.
em outras palavras, mostra diferentes combinações de fatores que podem ser comprados com uma certa quantia de dinheiro. A inclinação da linha iso-cost depende da relação entre preço do trabalho e preço do capital.
Por exemplo, um produtor que tem um orçamento total de ₹120, o que ele quer gastar com os fatores de produção, ou seja, X e Y. O preço de X no mercado é ₹15 por unidade, e o preço de Y é ₹10 por unidade. A tabela 7.5 mostra as combinações:
| Combinações | Unidades de X | Unidades de Y | Total das despesas |
|---|---|---|---|
| Um | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
A iso-custo da linha é mostrado na Figura 7.8:
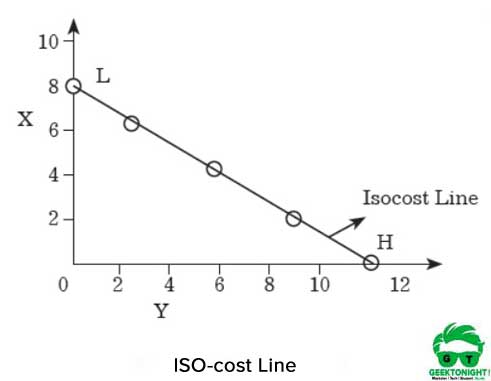
Como mostrado na Figura 6, se o produtor gasta todo o montante de dinheiro para a compra de X, então ele/ela pode comprar 8 unidades de X. por outro lado, se o produtor compras de Y com o valor total, então ele/ela seria capaz de chegar a 12 unidades.
se os pontos H E L forem unidos nos eixos X e Y, respectivamente, é obtida uma linha reta, que é chamada de linha de custo iso. Todas as combinações de X e Y que estão nesta linha, teria a mesma quantidade de custo que é ₹120.
da mesma forma, outras linhas de custo iso podem ser plotadas assumindo custos superiores a 120, caso o produtor esteja disposto a gastar mais dinheiro nos fatores de produção.
com a ajuda de linhas isoquant e iso-cost, um produtor pode determinar o ponto em que os insumos produzem lucro máximo incorrendo em custo mínimo. Tal ponto é denominado equilíbrio do produtor.
Leia Também: Cardinal e Ordinal Utilitário
Economia Empresarial Tutorial
(Clique no Tópico para Ler)
Vá, Compartilhe o artigo com os Amigos
Leave a Reply