31 formule matematice ACT trebuie să știți

geometrie plană

unghiuri și linii

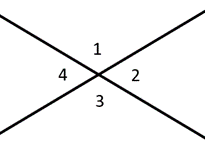
unghiurile de-a lungul unei linii se numesc unghiuri suplimentare, adunând până la \(180^{\circ}\). Unghiurile complementare se adaugă la \(90 ^ {\circ}\), un unghi drept. Unghiurile verticale descriu unghiuri direct unul față de celălalt, care sunt întotdeauna congruente. În diagrama din stânga, de exemplu, am spune că unghiurile 1 & 2 sunt suplimentare, în timp ce unghiurile 1 & 3 sunt unghiuri verticale.

aria unui triunghi

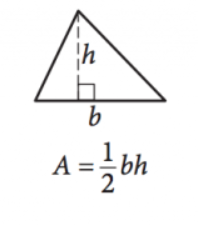
pentru imagine, multumim SAT

\(\frac{1}{2}bh=a\)

această ecuație oferă aria \((a)\) oricărui triunghi dat lungimile bazei \((b)\) și înălțimea \((h)\). Rețineți că înălțimea este lungimea liniei care se extinde la un unghi complementar din orice parte (baza) până la punctul/unghiul direct vizavi de acea parte.

pentru triunghiurile echilaterale, unde toate cele trei laturi \((s)\) au aceeași lungime, ecuația ariei este:

\ (\frac{s^2 \ sqrt{3}}{4} = A\)

Teorema lui Pitagora

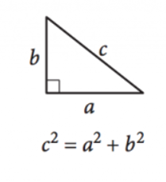
pentru imagine, multumim SAT

deoarece unghiurile dintr-un triunghi se adaugă întotdeauna la \(180^{\circ}\), un triunghi dreptunghiular este definit ca orice triunghi cu un unghi drept, asigurându-se că celelalte două unghiuri sunt complementare. Lungimile laterale ale triunghiurilor drepte pot fi definite de teorema lui Pitagora:

\ (a^2 + b^2 = c^2\)

aici, \(a\) și\ (b\) sunt lungimile picioarelor sau laturile vizavi de unghiurile complementare, iar\ (c\) este lungimea hipotenuzei, partea vizavi de unghiul drept.

poate fi util să memorați și următoarele Tripluri pitagoreice sau valori pentru lungimile laterale \((a,b, c)\): 3-4-5, 5-12-13, 7-24-25, și 8-15-17. Rețineți că hipotenuza este întotdeauna cea mai lungă parte.

triunghiuri drepte speciale

există două tipuri de triunghiuri drepte speciale, care au unghiurile și raporturile de lungime după cum urmează:

pentru imagine, multumim SAT

zone de patrulatere

\(a = lw\)

această formulă oferă aria unui dreptunghi cu lungimea \(l\) și lățimea \(w\).

\(a = bh\)

această formulă oferă aria unui paralelogram dat bază \(b\) , lungimea celor mai lungi laturi și înălțimea \(h\), definită ca lungimea liniei care se extinde la un unghi complementar de la o bază la alta.

\ (A=\frac{b_1+b_2}{2}\:\ori\:h\)

această formulă oferă aria unui trapez cu baze \(b_1\) și \(b_2\) și înălțime \(h\), definite în același mod ca și pentru paralelograme.

unghiurile interioare ale poligoanelor regulate

\((n-2)\:\times\:180^{\circ}= S\)

într-un poligon regulat, unde toate laturile și unghiurile sunt egale, această formulă oferă suma unghiurilor interioare date unui poligon cu \(n\) laturi și unghiuri. Putem găsi, de asemenea, fiecare unghi interior prin calcularea \(\frac{s}{n}\).

lungimea arcului într-un cerc

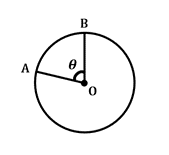
\(\frac {\theta}{360 ^ {\circ}}\: \ ori\:2 \ pi r = arc\: lungime\)

această formulă definește lungimea arcului sau secțiunea circumferinței cercului, între două raze date care se intersectează la centrul cercului cu unghiul central \(\theta\). Rețineți că \(2 \ pi r\) încorporează circumferința cercului în această formulă.

zona sectorului într-un cerc

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = sector\:zonă\)

Similar cu lungimea arcului, această formulă oferă aria sectorului între două raze date care se intersectează la centrul cercului cu unghiul central . \(\Pi r^2\) încorporează aria cercului în această formulă.

forme 3D

\(SA = 2 (lw + wh + lh)\)

\(V = lwh\)

aceste formule furnizează suprafața \((SA)\) și volumul \((V)\) pentru o prismă dreptunghiulară cu lungimea \(l\), Lățimea \(w\) și înălțimea \(h\).

\(v=\pi r^2h\)

aceasta este formula de volum pentru un cilindru drept cu raza de bază \(r\) și înălțimea \(h\).

dacă aveți nevoie de formulele de suprafață sau volum pentru orice alte forme 3D, actul va oferi formule relevante în întrebările în sine.

trigonometria

SOH-CAH-TOA

majoritatea problemelor ACT trig implică manipularea sinusului, cosinusului și tangentei, care sunt calculate după cum urmează pentru unghiul dat \(x\) într-un triunghi dreptunghiular:

\(sin(x)=\frac{opus\:picior}{hypotenuse}\)

\(cos (x) = \ frac{adiacent\: picior}{hypotenuse}\)

\(tan (x) = \ frac{opus\: picior}{adiacent\: picior}= \ frac{păcat (x)}{cos (x)}\)

SOH-CAH-TOA este un mnemonic ușor pentru amintirea funcției trig care corespunde lungimilor laterale!

identități de codificare

\(sin (x) = cos (90 ^ {\circ} – x)\)

\(cos ( x) = sin(90^{\circ}-x)\)

în cuvinte, aceste identități arată că o funcție trigonometrică a unghiului \(x\) este egală cu valoarea cofuncției complementului lui \(x\). Acestea sunt utilizate în general atunci când se ocupă de trigonometrie mai avansată, permițând conversii ușoare între sinus și cosinus.

Identități trigonometrice/reciproce

puteți vedea ocazional identitățile reciproce ale \(sin (x)\), \(cos (x)\) și \ (tan (x)\), care sunt:

\(csc(x) =\frac{1}{sin (x)}\)

\(sec (x) =\frac{1}{cos (x)}\)

\(cot (x) = \ frac{1}{tan (x)}\)

identitate pitagoreică

\(păcat^2 (x) + cos^2 (x)=1\)

pe baza teoremei pitagoreice și a cercului unitar, această identitate este folosită în general alături de identitățile cofunction pentru a rezolva probleme trigonometrice (sans calculator) unde unghiul \(x\) sau valorile acestor funcții trigonometrice ale \(x\) sunt necunoscute.

statistici și probabilitate

procente

\ (n\%\: of\: m = \ frac{n}{100}\:\times\:m\)

procentele sunt folosite pentru a exprima părți ale unui întreg, iar simbolul \(\%\) înseamnă în general “împărțiți la 100.”Ca atare, ecuația de mai sus răspunde oricărei probleme care solicită \(n\%\) din cantitate \(m\).

medie, mediană, mod și interval

ACT testează cunoștințele statistice de bază, implicând în general măsurile de mai jos:

• Media este media, sau \(\frac{sum\:of\: all\: terms}{total\:number\: of\:termeni}\)
• mediana este termenul mediu, sau media celor doi termeni medii dacă există un număr par de termeni
• modul este termenul(ele) care apare cel mai frecvent
• intervalul este diferența dintre termenii cei mai mari și cei mai mici

probabilitate

\(P(A) = \frac{număr\:de\:dorit\:rezultate}{total\:număr\:de\:posibil\:rezultate}\)

probabilitate reprezintă probabilitatea apariției unui eveniment \((a)\), calculată prin împărțirea numărului de rezultate dorite la numărul total de rezultate posibile. De exemplu, probabilitatea de rulare a unui 6 pe un zar uniform este \(\frac{1}{6}\).

evenimente independente

\(P(A\:și\:B) = P(A)\:\times\:P(B)\)

Evenimentele \(a\) și \(B\) sunt independente dacă \(a\) care apar nu afectează probabilitatea apariției \(B\). Pentru a calcula probabilitatea ca ambele evenimente independente să aibă loc, înmulțim probabilitățile lor individuale împreună. De exemplu, probabilitatea de a răsturna capetele de două ori este \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

înfășurându-l

am acoperit o mulțime de formule în acest post, dar asigurați-vă că revizuiți și toate conceptele matematice prin Algebra II și geometrie! De exemplu, vă puteți aștepta ca numerele complexe, vectorii, matricile, sistemele de ecuații și manipularea funcțiilor grafice să fie și ele la test. Consultați această descriere completă a secțiunii ACT math pentru mai multe informații.

amintiți-vă că practica face perfect, Mai ales pentru matematica! Veți dori să încercați o mulțime de probleme diferite înainte de ziua testului, cu scopul de a înțelege cu adevărat cum să aplicați și să integrați aceste concepte și formule în timp util.

pe măsură ce vi se permite un calculator pentru ACT, vă sfătuim să aduceți unul, dar cu un cuvânt de precauție. Amintiți-vă că fiecare problemă de matematică ACT poate fi rezolvată fără un calculator și este ușor să pierdeți timp prețios folosind calculatorul dvs. atunci când de fapt nu este nevoie. Ca atare, faceți secțiuni de practică temporizate cu calculatorul dvs. dacă intenționați să aduceți unul și amintiți-vă că este doar acolo în ultimă instanță: pentru a ușura calculele și de a crește viteza. Reach pentru el rar, și verificați dacă modelul dvs. specific este permis conform Politicii ACT calculator.