Curba Isoquant: definiție, proprietăți, tipuri, ipoteze
ce este curba Isoquant?
curba Izoquant: o relație tehnică care arată modul în care intrările sunt convertite în ieșire este reprezentată de o curbă izoquant. Acesta arată combinațiile optime de intrări de factori cu ajutorul prețurilor intrărilor de factori și a cantităților acestora care sunt utilizate pentru a produce aceeași ieșire.
termenul ISO implică egal și cuantic înseamnă cantitate sau ieșire.
de exemplu, pentru producerea a 100 de calendare se folosesc 90 de unități de capital și 10 unități de muncă.
curbele Isoquant sunt, de asemenea, numite curbe egale de produs sau curbe de indiferență de producție.
curba Izoquantului definiție
ipoteze ale curbei Izoquant
ipotezele unei curbe izoquant sunt după cum urmează:
- există doar doi factori de producție, forța de muncă și capitalul, pentru a produce un anumit produs.
- capitalul, munca și bunurile sunt divizibile în natură.
- capitalul și munca se pot substitui reciproc până la o anumită limită.
- tehnologia de producție este dată pe o perioadă de timp.
- factorii de producție sunt utilizați cu eficiență maximă.
să învățăm izoquant cu ajutorul tabelului următor.
Tabelul 1 prezintă diferitele combinații de doi factori de intrare, și anume forța de muncă și capitalul pentru producerea a 150 de tone de producție:
| muncă | Capital |
|---|---|
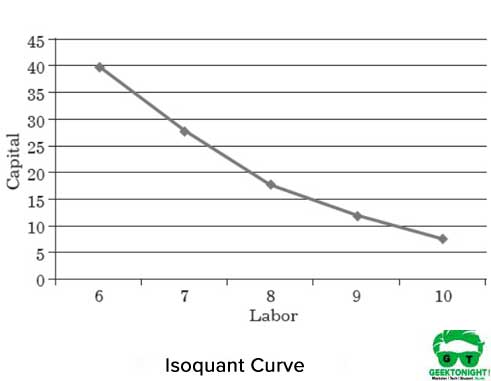
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
Figura 1 prezintă curba izoquantă a diferitelor combinații de capital de muncă care ajută la producerea a 150 de tone de producție:
proprietățile curbei Izoquant
unele dintre proprietățile curbei izoquant sunt după cum urmează:
- curbe Izoquant pantă în jos
- curbe Izoquant sunt convexe la origine
- curbe Izoquant nu se pot intersecta reciproc
- mai mare izoquant mai mare ieșire

curbele Izoquant înclină în jos
aceasta implică faptul că panta curbei izoquant este negativă. Acest lucru se datorează faptului că atunci când capitalul (K) este crescut, cantitatea de muncă (L) este redusă sau invers, pentru a menține același nivel de producție.
curbele Izoquante sunt convexe la origine
implică faptul că intrările factorilor nu sunt înlocuitori perfecți. Această proprietate arată înlocuirea intrărilor și diminuarea ratei marginale de substituție tehnică a izoquantului. Semnificația marginală a unei intrări (capital) în termeni de altă intrare (muncă) se diminuează împreună cu curba izoquant.
Figura 2 prezintă curba izoquantă convexă:
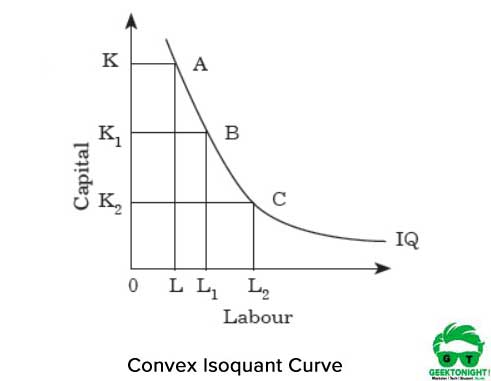
convexitatea reprezintă faptul că MRT-urile se diminuează dacă trecem de la punctul A la B și de la B la C de-a lungul izoquantului. MRTS se diminuează deoarece cele două intrări munca și capitalul nu sunt înlocuitori perfecți.
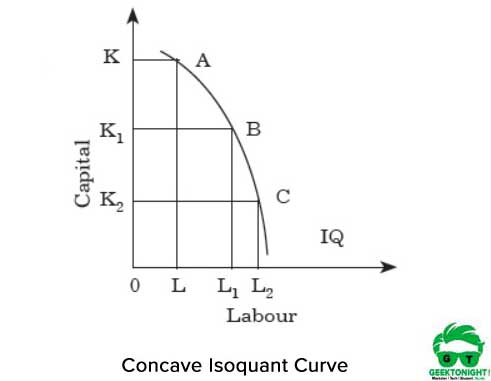
astfel, pentru fiecare creștere a forței de muncă, există o scădere a capitalului. Dacă izoquantul este concav, MRTS-ul muncii pentru capital crește. Figura 3 prezintă curba izoquantului concav:
așa cum se arată în Figura 3, dacă ne deplasăm de la punctul A la B și de la B la C de-a lungul izoquantului, MRTS crește. Acesta arată că cele două intrări munca și capitalul sunt înlocuitori perfecți. Astfel, pentru fiecare creștere a forței de muncă, există o creștere a capitalului.
curbele Izoquant nu se pot intersecta între ele
un izoquant implică diferitele niveluri de combinație care produc diferite niveluri de intrări. Dacă izoquanții se intersectează reciproc, ar implica faptul că o singură combinație de intrare poate produce două niveluri de ieșire, ceea ce nu este posibil. Legea producției nu ar fi aplicabilă.
mai mare izoquant mai mare ieșire
aceasta implică faptul că izoquant mai mare reprezintă ieșire mai mare. Curba superioară a izoquantului produce mai multă ieșire decât curba de dedesubt. Acest lucru se datorează faptului că combinația mai mare de intrare are ca rezultat o ieșire mai mare în comparație cu curba care se află sub ea.
rata marginală de substituție tehnică
panta curbei izoquant este rata de substituție care arată modul în care o intrare poate fi înlocuită cu alta în timp ce menține constanta de ieșire. Aceasta se numește rata marginală de substituție tehnică (MRTS).
potrivit lui Lipsey, “rata marginală de substituție tehnică poate fi definită ca rata la care un factor este înlocuit cu altul cu producția menținută constantă.”
formula pentru calcularea MRTS este următoarea:
MRTS = – la un anumit nivel de producție, MRTS de capital pentru muncă ar implica cantitatea de muncă la care firma ar fi dispusă să renunțe pentru o unitate suplimentară de capital. În mod similar, MRT-urile de muncă pentru capital ar implica suma de capital pe care firma ar fi dispusă să o renunțe pentru o unitate de muncă suplimentară.
MRTS este, de asemenea, egal cu raportul dintre produsul marginal al unei intrări și produsul marginal al unei alte intrări. Ieșirea de-a lungul izoquantului este constantă. Dacă schimbarea muncii este înlocuită cu schimbarea capitalului, atunci creșterea producției datorată creșterii muncii ar trebui să se potrivească cu scăderea producției datorată scăderii capitalului. Din punct de vedere matematic
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Deoarece producția rămâne neschimbată la un anumit isoquant,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
Astfel, putem spune că MRTS dintre intrări este egal cu marginal produse de intrări.
MRTS se calculează conform tabelului 2
| muncă | Capital | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
tipuri de curbe Izoquante
există o substituție continuă a unei variabile de intrare cu cealaltă variabilă de intrare la o rată de diminuare. Complementele perfecte și înlocuitorii perfecți dau diferite forme de izoquante.
diferitele tipuri de curbe izoquant sunt după cum urmează:
- Izoquant liniar
- izoquant în formă de L

Izoquant liniar
este o izoquant în linie dreaptă și reprezintă o substituibilitate perfectă între intrările, capitalul și munca funcției de producție. MRTS între intrări rămâne constantă. Figura 4 prezintă un izoquant liniar:
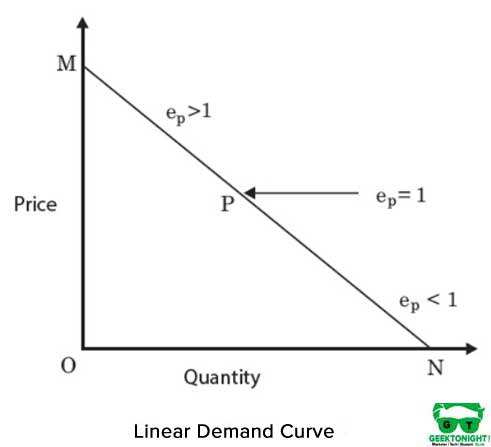
forma algebrică a funcției de producție în cazul izoquantului liniar este următoarea:
Q = Ak + BL
aici, Q este suma ponderată a K și L. panta curbei poate fi calculată cu ajutorul următoarei formule:
MPK = XQ/XQQ = a
MPL = XQQ/XQQ = B
MRTS = MPL / XQQ
MRTS = – b/a (b/a este constantă)
cu toate acestea, izoquantul liniar nu există în lumea reală.
izoquant în formă de l
acesta este cazul complementelor perfecte. În acest sens, combinația dintre capital și muncă este într-o proporție fixă. O singură combinație de muncă și capital este posibilă pentru a produce un produs cu o proporție aplicată de inputuri.
pentru creșterea producției, o organizație trebuie să crească ambele intrări proporțional. Reprezentarea grafică a proporției factorului fix isoquant este l în formă, prezentată în Figura 5:
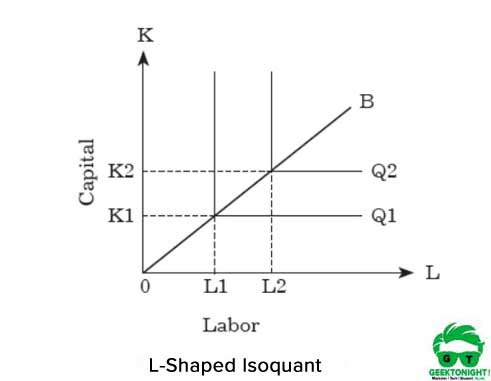
după cum se arată în Figura 5, izoquantul în formă de L reprezintă faptul că nu există nicio substituție între muncă și capital și se presupune că acestea sunt bunuri complementare. Se poate observa că unitățile de capital OK1 și unitățile de muncă OL1 sunt necesare pentru producerea Q1.
pe de altă parte, pentru a crește producția de la Q1 la Q2, o organizație trebuie să crească intrările de la K1 la K2 și L1 la L2 ambele. Această relație între capital și muncă poate fi exprimată după cum urmează:
Q = f (K, L) = min (aK, bL)
unde, min implică Q egal cu cel mai mic dintre cei doi termeni, aK și bL
de exemplu, în cazul aK > bL, atunci Q = bL și în cazul aK < bL atunci, Q = ak.
acest isoquant este la fel ca funcția de producție leontif.
elasticitatea substituției între factori
știm că MRTS este panta izoquantului. Cu toate acestea, nu dezvăluie gradul de substituibilitate a unui factor la altul. Este important să se măsoare gradul de substituibilitate între cele două intrări.
prin urmare, economiștii au dezvoltat o formulă pentru estimarea gradului de substituibilitate între cele două intrări, capital și muncă, care este cunoscută sub numele de elasticitatea substituției factorilor.
elasticitatea substituției factorului (XV) se referă la raportul dintre variația procentuală a raportului capital-muncă și variația procentuală a MRTS.
este reprezentat matematic după cum urmează:
XV = variația procentuală a raportului muncii de capital/variația procentuală a MRTS
sau,
*
dacă: * * * * * * * * * * * ; σ = 1
Dacă ∆K/∆L > ∆MRTS ; σ > 1
Dacă ∆K/∆L < ∆MRTS ; σ < 1
Mare elasticitatea de substituție între factori sugerează că factorii pot fi ușor înlocuite la fiecare alte, în timp ce o elasticitate scăzută reprezintă această substituire de factori, este posibil într-o anumită măsură.
în cazul izoquantului liniar, elasticitatea de substituție ar fi infinită, iar în cazul izoquanților în formă de L, ar fi zero.
curbe de cost ISO
curba de cost Iso este locul punctelor din toate combinațiile diferite de muncă și capital pe care o organizație le poate folosi, având în vedere prețul acestor intrări. Linia Iso-cost reprezintă prețul factorilor împreună cu suma de bani pe care o organizație este dispusă să o cheltuiască pentru factori.
cu alte cuvinte, arată diferite combinații de factori care pot fi achiziționați la o anumită sumă de bani. Panta liniei iso-cost depinde de raportul dintre prețul muncii și prețul capitalului.
de exemplu, un producător are un buget total de 120 de dolari, pe care dorește să-l cheltuiască pe factorii de producție, și anume, X și Y. prețul lui X pe piață este de 15 dolari pe unitate, iar prețul lui Y este de 10 dolari pe unitate. Tabelul 7.5 prezintă combinațiile:
| combinații | unități de X | unități de Y | cheltuieli totale |
|---|---|---|---|
| A | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
linia iso-cost este prezentată în figura 7.8:
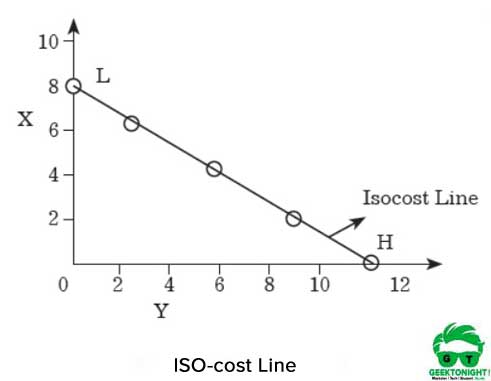
după cum se arată în Figura 6, dacă producătorul cheltuiește întreaga sumă de bani pentru a cumpăra X, atunci el/ea poate achiziționa 8 unități de X. Pe de altă parte, dacă producătorul cumpără Y cu întreaga sumă, atunci el/ea ar putea obține 12 unități.
dacă punctele H și L sunt unite pe axele X și respectiv Y, atunci se obține o linie dreaptă, care se numește linie iso-cost. Toate combinațiile de X și Y, care se află pe această linie, ar avea aceeași sumă de cost, care este de 120.
în mod similar, alte linii iso-cost pot fi reprezentate prin luarea unui cost mai mare de 120, în cazul în care producătorul este dispus să cheltuiască mai mulți bani pe factorii de producție.
cu ajutorul liniilor izoquant și iso-cost, un producător poate determina punctul în care intrările produc profit maxim prin suportarea costului minim. Un astfel de punct este denumit echilibrul producătorului.
Citește Și: Cardinal și Ordinal utilitate
Afaceri Economie Tutorial
(Click pe subiect pentru a citi)
continuați, partajați articolul cu prietenii
Leave a Reply