31 ACT matematiska formler du behöver veta

Plangeometri

vinklar och linjer

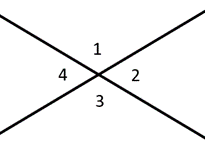
vinklar längs en linje kallas kompletterande vinklar och lägger till upp till \(180^{\circ}\). Kompletterande vinklar lägger till upp till \(90^{\circ}\), en rät vinkel. Vertikala vinklar beskriver vinklar mittemot varandra, som alltid är kongruenta. I diagrammet till vänster skulle vi till exempel säga att vinklar 1 & 2 är kompletterande, medan vinklar 1 & 3 är vertikala vinklar.

område av en triangel

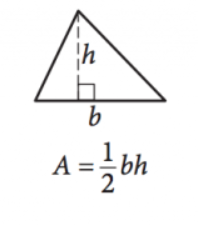
bild med tillstånd av SAT

\(\frac{1}{2}bh=a\)

denna ekvation ger området\ ((a)\) av någon triangel givna längder av basen\ ((b)\) och höjd\((h)\). Observera att höjden är längden på linjen som sträcker sig i en komplementär vinkel från vilken sida som helst (basen) upp till punkten/vinkeln mittemot den sidan.

för liksidiga trianglar, där alla tre sidor \((s)\) är lika långa, är arealekvationen:

\(\frac{s^2\sqrt{3}}{4} = A\)

Pythagoras sats

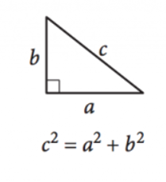
bild med tillstånd av SAT

eftersom vinklar i en triangel alltid lägger till \(180^{\circ}\) definieras en rätt triangel som vilken triangel som helst med en rätt vinkel, vilket säkerställer att de andra två vinklarna är komplementära. Sidolängderna på högra trianglar kan definieras av Pythagoras sats:

\(a^2 + b^2=c^2\)

här är\ (a\) och\ (b\) längderna på benen, eller sidorna tvärs över de komplementära vinklarna, och\ (c\) är längden på hypotenusen, sidan tvärs över från rätt vinkel.

det kan vara till hjälp att också memorera följande Pythagoras tripplar eller värden för sidlängder \((a,b, c)\): 3-4-5, 5-12-13, 7-24-25, och 8-15-17. Observera att hypotenusen alltid är den längsta sidan.

Special right Triangles

det finns två typer av special right triangles, som har vinklarna och längdförhållandena enligt följande:

bild med tillstånd av SAT

områden av Quadrilaterals

\(A = lw\)

denna formel ger området för en rektangel med Längd \(l\) och bredd \(w\).

\(a = bh\)

denna formel ger området för ett parallellogram som ges bas \(b\) , längden på de längsta sidorna och höjden \(h\), definierad som längden på linjen som sträcker sig i en komplementär vinkel upp från en bas till den andra.

\(A= \ frac{b_1 + b_2}{2}\: \ gånger\:h\)

denna formel ger området för en trapezoid med baserna\ (b_1\) och\ (b_2\) och höjd\ (h\), definierade på samma sätt som för parallellogram.

inre vinklar av vanliga polygoner

\((n-2)\:\times\:180^{\circ}= s\)

i en vanlig polygon, där alla sidor och vinklar är lika, ger denna formel summan \((S)\) av de inre vinklarna som ges en polygon med \(n\) sidor och vinklar. Vi kan också hitta varje inre vinkel genom att beräkna \(\frac{s}{n}\).

båglängd i en cirkel

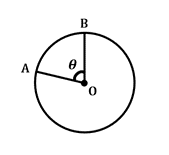
\(\frac {\theta}{360^{\circ}}\: \ gånger\:2 \ pi r=arc\: length\)

denna formel definierar längden på bågen, eller sektionen av cirkelomkretsen, mellan två givna radier som skär i cirkelcentret med central vinkel \(\theta\). Observera att \(2 \ pi r\) innehåller cirkelomkrets i denna formel.

sektorområde i en cirkel

\(\frac{\theta}{360^{\circ}}\:\times\:\pi r^2 = sektor\:area\)

i likhet med båglängd ger denna formel området för sektorn mellan två givna radier som skär varandra i cirkelcentret med central vinkel . \(\Pi r^2\) innehåller cirkelområdet i denna formel.

3D-former

\(SA = 2 (lw + wh + lh)\)

\(v= lwh\)

dessa formler ger ytan \((SA)\) och volymen \((V)\) för ett rektangulärt prisma med Längd \(l\), bredd \(w\) och höjd \(h\).

\(V=\pi r^2h\)

detta är volymformeln för en höger cylinder med basradie \(r\) och höjd \(h\).

om du behöver ytarea eller volymformler för andra 3D-former, kommer lagen att ge relevanta formler i själva frågorna.

Trigonometri

SOH-CAH-TOA

de flesta ACT trig-problem innebär att man manipulerar sinus, cosinus och tangent, som beräknas enligt följande för given vinkel \(x\) i en rätt triangel:

\(sin (x)= \ frac{motsatt\: ben}{hypotenuse}\)

\(cos (x)=\frac{angränsande\:ben}{hypotenusan}\)

\(tan (x)= \ frac{motsatt\: ben}{angränsande\:ben}=\frac{sin(x)}{cos (x)}\)

SOH-CAH-TOA är en lätt mnemonic för att komma ihåg vilken trig-funktion som motsvarar vilka sidlängder!

Kofunktionsidentiteter

\(sin (x) = cos (90^{\circ} – x)\)

\(cos (x) = sin(90^{\circ}-x)\)

i ord visar dessa identiteter att en trig-funktion av vinkel \(x\) är lika med värdet av kofunktionen för komplementet av \(x\). De används vanligtvis när man hanterar mer avancerad trigonometri, vilket möjliggör enkla omvandlingar mellan sinus och cosinus.

Ratio / Reciprocal Trig identiteter

du kan ibland se de ömsesidiga identiteterna för \(sin (x)\), \(cos (x)\) och \(tan (x)\), som är:

\(csc (x) = \ frac{1}{sin (x)}\)

\(sek (x) = \ frac{1}{cos (x)}\)

\(cot (x) = \ frac{1}{tan (x)}\)

Pythagoras identitet

\(synd^2 (x) + cos^2 (x)=1\)

baserat på Pythagoras sats och enhetscirkeln används denna identitet vanligtvis tillsammans med kofunktionsidentiteterna för att lösa trig-problem (sans calculator) där vinkel \(x\) eller värdena för dessa trig-funktioner av \(x\) är okända.

statistik och sannolikhet

procentsatser

\(n\%\: av\: m = \ frac{n}{100}\: \ gånger\:m\)

procentsatser används för att uttrycka delar av en helhet, och symbolen \ ( \ % \ ) betyder i allmänhet “dividera med 100.”Som sådan svarar ovanstående ekvation alla problem som ber om\ (n\%\) av kvantitet\(m\).

medelvärde, Median, läge och intervall

lagen testar grundläggande statistisk kunskap, som i allmänhet involverar åtgärderna nedan:

• medelvärdet är medelvärdet, eller \(\frac{sum\: of\: all\: terms}{total\: number\: of\:termer}\)
• Median är mellantermen, eller medelvärdet av de två mellantermerna om det finns ett jämnt antal termer
• läge är termen(erna) som förekommer oftast
• intervall är skillnaden mellan de största och minsta termerna

Sannolikhet

\(P(A) = \frac{number\:of\:desired\:outcomes}{total\:number\:of\:possible\:outcomes}\)

Sannolikhet representerar sannolikheten för att en händelse \((a)\) inträffar, beräknad genom att dividera antalet önskade resultat med antalet totala möjliga resultat. Till exempel är sannolikheten att rulla en 6 på en jämn tärning \(\frac{1}{6}\).

oberoende händelser

\(P(A\:och\:B) = P(A)\:\gånger\:P(B)\)

händelser \(A\) och \(B\) är oberoende om \(A\) inträffar inte påverkar sannolikheten för \(B\) inträffar. För att beräkna sannolikheten för att båda oberoende händelserna kommer att inträffa multiplicerar vi deras individuella sannolikheter tillsammans. Till exempel är sannolikheten att vända huvuden två gånger \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).

Linda upp det

vi har täckt massor av formler i det här inlägget, men se till att också granska alla matematiska begrepp genom Algebra II och geometri! Till exempel kan du förvänta dig komplexa tal, vektorer, matriser, ekvationssystem och manipulera grafiska funktioner för att vara på testet också. Se den här fullständiga beskrivningen av ACT math-avsnittet för mer info.

kom ihåg att övning ger färdighet, särskilt för matematik! Du vill prova många olika problem före testdagen, med målet att verkligen förstå hur man tillämpar och integrerar dessa begrepp och formler i tid.

eftersom du får en kalkylator för lagen, rekommenderar vi att du tar med en, men med ett varningens ord. Kom ihåg att varje ACT math-problem kan lösas utan en räknare, och det är lätt att slösa bort värdefull tid genom att använda din räknare när du faktiskt inte behöver. Som sådan, gör tidsinställda övningsavsnitt med din räknare om du planerar att ta med en, och kom ihåg att det bara är där som en sista utväg: för att underlätta beräkningar och öka din hastighet. Nå för det sällan, och kontrollera att din specifika modell är tillåten enligt ACT calculator policy.