Isoquant kurva: Definition, egenskaper, typer, antaganden
Vad är Isoquant Curve?
Isoquant Curve: en teknisk relation som visar hur ingångar omvandlas till utgång avbildas av en isoquant kurva. Den visar de optimala kombinationerna av faktoringångar med hjälp av priser på faktoringångar och deras kvantiteter som används för att producera samma produktion.
termen ISO innebär lika och quant betyder kvantitet eller utgång.
till exempel, för att producera 100 kalendrar, 90 enheter kapital och 10 enheter arbete används.
Isoquant kurvor kallas också som lika produktkurvor eller produktion likgiltighetskurvor.
Isoquant Curve Definition
antaganden om Isoquantkurva
antagandena för en isoquantkurva är följande:
- det finns bara två faktorer, arbete och kapital, för att producera en viss produkt.
- kapital, arbete och varor är delbara till sin natur.
- kapital och arbete kan ersätta varandra upp till en viss gräns.
- produktionsteknik ges under en tidsperiod.
- produktionsfaktorer används med full effektivitet.
Låt oss lära oss isoquant med hjälp av följande tabell.
Tabell 1 visar de olika kombinationerna av tvåfaktorinsatser, nämligen arbete och kapital för att producera 150 ton produktion:
| arbete | kapital |
|---|---|
| 6 | 40 |
| 7 | 28 |
| 8 | 18 |
| 9 | 12 |
| 10 | 8 |
Figur 1 visar isoquantkurvan för olika arbetskapitalkombinationer som hjälper till att producera 150 ton produktion:
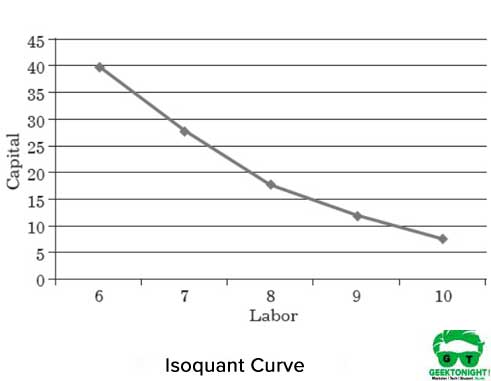
egenskaper hos Isoquant Curve
några av egenskaperna hos isoquant curve är följande:
- Isoquant kurvor lutning nedåt
- Isoquant kurvor är konvexa till Ursprung
- Isoquant kurvor kan inte korsa varandra
- högre isoquant ju högre utgång

Isoquant kurvor lutning nedåt
det innebär att lutningen på isoquant kurvan är negativ. Detta beror på att när kapitalet (K) ökas, minskas arbetsmängden (L) eller vice versa för att hålla samma produktionsnivå.
Isoquant kurvor är konvexa till Ursprung
det innebär att faktoringångar inte är perfekta substitut. Den här egenskapen visar substitutionen av ingångar och minskande marginalhastighet för teknisk substitution av isoquant. Den marginella betydelsen av en ingång (kapital) i termer av en annan ingång (arbete) minskar tillsammans med isoquantkurvan.
Figur 2 visar den konvexa isoquantkurvan:
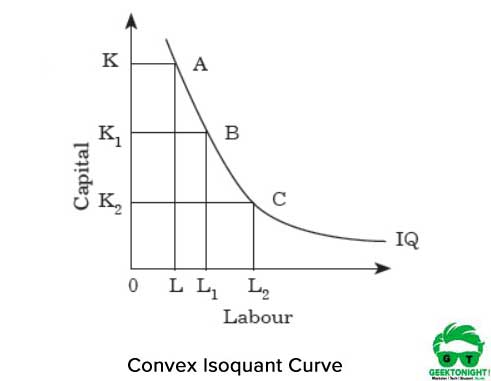
konvexiteten representerar att MRTS minskar om vi flyttar från punkt A till B och från B till C längs isoquanten. MRTS minskar eftersom de två insatserna arbete och kapital inte är perfekta substitut.
för varje ökning av arbetet sker således en minskning av kapitalet. Om isokvanten är konkav, ökar arbetets MRTS för kapitalet. Figur 3 visar den konkava isoquantkurvan:
som visas i Figur 3, Om vi flyttar från punkt A till B och från B till C längs isoquanten, ökar MRTS. Det visar att de två insatserna arbete och kapital är perfekta substitut. För varje ökning av arbetet sker alltså en ökning av kapitalet.
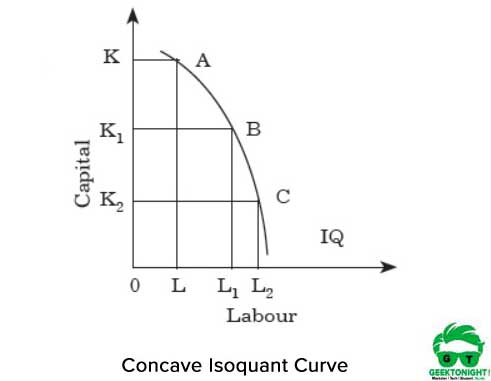
Isoquantkurvor kan inte korsa varandra
en isoquant innebär olika nivåer av kombination som producerar olika nivåer av ingångar. Om isoquanterna skär varandra skulle det innebära att en enda ingångskombination kan producera två utgångsnivåer, vilket inte är möjligt. Produktionslagen skulle inte vara tillämplig.
högre isoquant ju högre output
det innebär att den högre isoquant representerar högre output. Den övre kurvan för isoquanten ger mer effekt än kurvan under. Detta beror på att den större kombinationen av ingång resulterar i en större utgång jämfört med kurvan som ligger under den.
Marginalhastighet för teknisk Substitution
lutningen på isoquantkurvan är substitutionshastigheten som visar hur en ingång kan ersättas med en annan medan du håller utmatningen konstant. Detta kallas marginal rate of technical substitution (MRTS).
enligt Lipsey kan “marginalhastigheten för teknisk substitution definieras som den hastighet med vilken en faktor ersätts med en annan med en konstant produktion.”
formeln för beräkning av MRTS är som följer:
MRTS = – C / C L
där, c k = förändring i kapital
C L= förändring i arbete
formeln visar att vid en given produktionsnivå skulle MRTS av kapital för arbete innebära den mängd arbete som företaget skulle vara villigt att ge upp för en ytterligare kapitalenhet. På samma sätt skulle MRTS av arbete för kapital innebära den mängd kapital som företaget skulle vara villigt att ge upp för en ytterligare arbetsenhet.
MRTS är också lika med förhållandet mellan marginalprodukt från en ingång och marginalprodukten från en annan ingång. Utgången längs isoquanten är konstant. Om förändringen av arbetet ersätts med förändringen av kapitalet, då bör ökningen av produktionen på grund av ökningen av arbetet motsvara minskningen av produktionen på grund av minskningen av kapitalet. Matematiskt
∆L x MPL= ∆K x MPk
∆Q= ∆L x MPL + ∆K x MPk
Eftersom produktionen är oförändrad vid en given isoquant,
∆L x MPL + ∆K x MPk = 0
(MPL / MPK)= (- ∆K / ∆L)
MRTSKL = (MPL / MPK)
vi kan Alltså säga att MRTS mellan ingångarna är lika med marginell produkter av ingångarna.
MRTS beräknas enligt Tabell 2
| arbetskraft | kapital | MRTS |
|---|---|---|
| 6 | 40 | |
| 7 | 28 | 12:1 |
| 8 | 18 | 10:1 |
| 9 | 12 | 6:1 |
| 10 | 8 | 4:1 |
typer av Isoquantkurva
det finns en kontinuerlig substitution av en ingångsvariabel med den andra ingångsvariabeln vid en minskande hastighet. Perfekta komplement och perfekta ersättare ger olika former av isoquants.
de olika typerna av isoquantkurva är följande:
- linjär isoquant
- L-formad isoquant

linjär isoquant
det är en rak linje isoquant och representerar en perfekt substituerbarhet mellan produktionsfunktionens ingångar, kapital och arbete. MRTS mellan ingångar förblir konstant. Figur 4 visar en linjär isoquant:
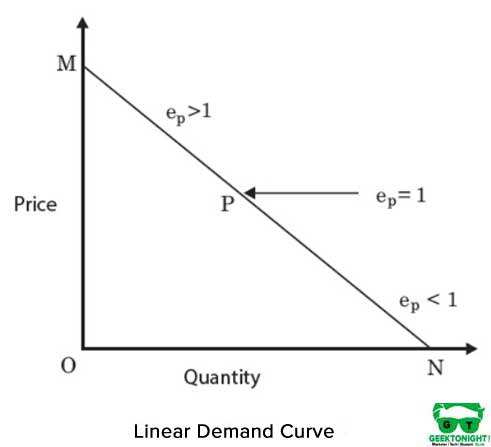
den algebraiska formen av produktionsfunktion vid linjär isoquant är följande:
Q = ak + BL
här är Q den viktade summan av K och L. kurvens lutning kan beräknas med hjälp av följande formel:
MPK = ug Q / ug K = a
MPL = ug Q / ug L = B
MRTS = ug/MPK
MRTS = -B/a (b / A är konstant)
linjär isoquant har emellertid inte existens i den verkliga världen.
L-formad isoquant
detta är fallet med perfekta komplement. Däri ligger kombinationen mellan kapital och arbete i en fast proportion. Endast en kombination av arbete och kapital är möjlig att producera en produkt med anbringad andel insatsvaror.
för att öka produktionen måste en organisation öka båda insatserna proportionellt. Den grafiska representationen av isoquant med fast faktorandel är L i form, visas i Figur 5:
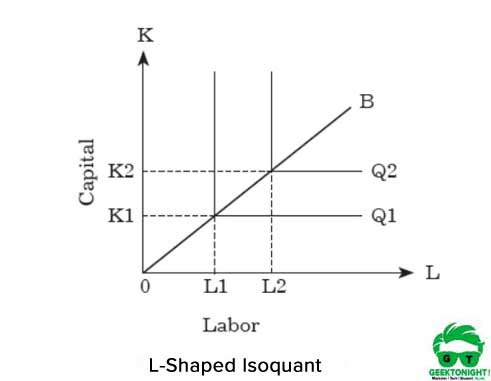
som visas i Figur 5 representerar den L-formade isoquanten att det inte finns någon substitution mellan arbete och kapital och de antas vara kompletterande varor. Det kan ses att OK1 kapitalaggregat och OL1 arbetsenheter krävs för produktion av Q1.
å andra sidan, för att öka produktionen från Q1 till Q2, behöver en organisation öka insatserna från K1 till K2 och L1 till L2 båda. Detta förhållande mellan kapital och arbete kan uttryckas enligt följande:
Q = f (K, L) = min (aK, bL)
var, min innebär Q lika med lägre av de två termerna, aK och bL
till exempel, i fall aK > bL, då Q = bL och i fall ak < bL då, Q = ak.
denna isoquant är samma som leontif produktionsfunktion.
elasticitet av Substitution mellan faktorer
vi vet att MRTS är isoquantens lutning. Det avslöjar emellertid inte graden av substituerbarhet av en faktor till en annan. Det är viktigt att mäta graden av substituerbarhet mellan de två ingångarna.
därför har ekonomer utvecklat en formel för att uppskatta omfattningen av substituerbarhet mellan de två insatserna, kapital och arbete, som kallas elasticitet för faktorsubstitution.
elasticiteten hos faktorsubstitutionen (IC) avser förhållandet mellan procentuell förändring av kapital-arbetsförhållandet och procentuell förändring av MRTS.
den representeras matematiskt på följande sätt:
Brasilien = procentuell förändring av kapitalarbetsförhållandet / procentuell förändring av MRTS
eller,
*
om K / 2075 ; σ = 1
Om ∆K/∆L > ∆MRTS ; σ > 1
Om ∆K/∆L < ∆MRTS ; σ < 1
Hög elasticitet av substitution mellan faktorer innebär att de faktorer som lätt kan ersätta varandra, medan en låg elasticitet innebär att ett utbyte av faktorer är möjligt att i viss utsträckning.
vid linjär isoquant skulle substitutionselasticiteten vara oändlig, och vid L-formade isoquants skulle den vara noll.
ISO-Kostnadskurvor
Iso-kostnadskurva är platsen för punkter för alla olika kombinationer av arbete och kapital som en organisation kan använda, med tanke på priset på dessa ingångar. Iso-cost line representerar priset på faktorer tillsammans med hur mycket pengar en organisation är villig att spendera på faktorer.
med andra ord visar det olika kombinationer av faktorer som kan köpas till en viss summa pengar. Isokostnadslinjens lutning beror på förhållandet mellan arbetets pris och kapitalets pris.
till exempel, en producent har en total budget på 120 x, som han vill spendera på produktionsfaktorer, nämligen X och Y. priset på x på marknaden är 15 x per enhet och priset på Y är 10 x per enhet. Tabell 7.5 visar kombinationerna:
| kombinationer | enheter av X | enheter av Y | totala utgifter |
|---|---|---|---|
| A | 8 | 0 | 120 |
| B | 6 | 3 | 120 |
| C | 4 | 6 | 120 |
| D | 2 | 9 | 120 |
| E | 0 | 12 | 120 |
ISO-kostnadslinjen visas i Figur 7.8:
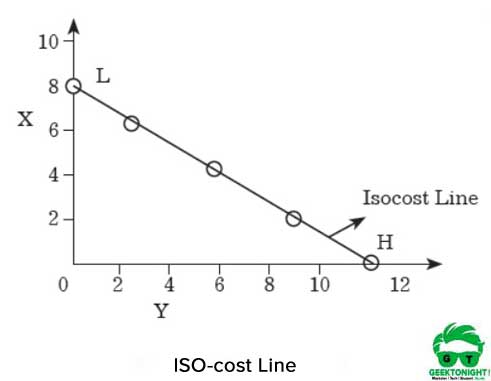
som visas i Figur 6, om producenten spenderar hela summan av pengar för att köpa X, kan han/hon köpa 8 enheter av X. å andra sidan, om producenten köper Y med hela beloppet, skulle han/hon kunna få 12 enheter.
om punkterna H och L förenas på X-respektive Y-axlarna erhålls en rak linje, som kallas iso-kostnadslinje. Alla kombinationer av X och Y som ligger på denna linje, skulle ha samma mängd kostnad som är 120.
på samma sätt kan andra iso-kostnadslinjer ritas genom att kosta mer än 120, om Producenten är villig att spendera mer pengar på produktionsfaktorerna.
med hjälp av isoquant-och iso-kostnadslinjer kan en producent bestämma den punkt där insatsvaror ger maximal vinst genom att ådra sig minimikostnader. En sådan punkt kallas producentens jämvikt.
Läs Också: Kardinal och ordinär nytta
Företagsekonomi handledning
(klicka på ämnet för att läsa)
Fortsätt, Dela artikel med vänner
Leave a Reply