topp 3 Vanligaste Inventory Control Policies

den här bloggen definierar och jämför de tre vanligaste inventory control policies. Det bör vara till hjälp både för de nya på fältet och även för erfarna personer som överväger en eventuell förändring av företagets policy. Bloggen överväger också hur efterfrågeprognoser stöder lagerhantering, val av vilken policy som ska användas och beräkning av de ingångar som driver dessa policyer. Tänk på det som en förkortad inventering 101.

Scenario

du hanterar ett visst objekt. Objektet är tillräckligt viktigt för dina kunder att du vill ha tillräckligt med lager för att undvika att lagra ut. Objektet är dock också dyrt nog att du också vill minimera mängden kontanter som är bundna i lager. Processen att beställa påfyllningslager är tillräckligt dyr och besvärlig att du också vill minimera antalet inköpsorder du måste generera. Efterfrågan på objektet är oförutsägbar. Så är påfyllningstiden mellan när du upptäcker behovet av mer och när det kommer på hyllan redo för användning eller leverans.

din fråga är ” hur hanterar jag det här objektet? Hur bestämmer jag när jag ska beställa mer och hur mycket jag ska beställa?”När du fattar detta beslut finns det olika tillvägagångssätt du kan använda. Den här bloggen beskriver de vanligaste lagerplaneringspolicyerna: periodisk ordning upp till (T, S), Ombeställ punkt/orderkvantitet (R, Q) och Min/Max (s, S). Dessa tillvägagångssätt är ofta inbäddade i ERP-system och gör det möjligt för företag att generera automatiska förslag på vad och när de ska beställa. För att fatta rätt beslut måste du veta hur var och en av dessa tillvägagångssätt är utformade för att fungera och fördelarna och begränsningarna för varje tillvägagångssätt.

periodisk granskning, order-up-to policy

den korta notationen för denna policy är (T, S), där T är den fasta tiden mellan order och S är order-up-to-level.

när man beställer: beställningar placeras som urverk varje t-dag. Användningen av ett fast omordningsintervall är till hjälp för företag som inte kan hålla reda på sin lagernivå i realtid eller som föredrar att utfärda order till leverantörer med schemalagda intervall.

hur mycket att beställa: lagernivån mäts och gapet beräknas mellan den nivån och order-upp-till nivå S. Om lagernivån är 7 enheter och S = 10, beställs 3 enheter.

kommentar: Detta är den enklaste policyn att genomföra men också den minst smidiga för att svara på fluktuationer i efterfrågan och/eller ledtid. Observera också att även om orderstorleken skulle vara tillräcklig för att returnera lagernivån till S om påfyllning var omedelbar, kommer det i praktiken att finnas en viss påfyllningsfördröjning under vilken tid inventeringen fortsätter att sjunka, så lagernivån kommer sällan att nå hela vägen upp S.

kontinuerlig granskning, fast orderkvantitetspolicy (Omordningspunkt, orderkvantitet)

stenografi notationen för denna policy är (R, Q), där R är omordningspunkten och Q är den fasta orderkvantiteten.

när ska man beställa: Beställningar placeras så snart inventeringen sjunker till eller under omordningspunkten, R. i teorin kontrolleras lagernivån ständigt, men i praktiken kontrolleras den vanligtvis regelbundet i början eller slutet av varje arbetsdag.

hur mycket att beställa: orderstorleken är alltid fast vid Q-enheter.

kommentar: (R, Q) är mer lyhörd än (S, T) eftersom det reagerar snabbare på tecken på överhängande stockout. Värdet på den fasta orderkvantiteten Q kanske inte är helt upp till dig. Ofta kan leverantörer diktera villkor som begränsar ditt val av Q till värden som är kompatibla med minima och multiplar. Till exempel kan en leverantör insistera på en order på minst 20 enheter och alltid vara en multipel av 5. Således order storlekar måste vara antingen 20, 25, 30, 35, etc. (Denna kommentar gällde också de två andra inventeringspolicyerna.)

kontinuerlig granskning, order-up-to-policy (Min/Max)

stenografi notationen för denna policy är (s, S), ibland kallad “little s, big s” där s är omordningspunkten och S är order-up-to-level. Denna policy kallas oftare (Min, Max).

när ska man beställa: beställningar placeras så snart inventeringen sjunker till eller under Min. Som med (R, Q) övervakas lagernivån ständigt, men i praktiken kontrolleras den vanligtvis i slutet av varje arbetsdag.

hur mycket att beställa: Orderstorleken varierar. Det är lika med klyftan mellan Max och den aktuella inventeringen i det ögonblick som Min uppnås eller bryts.

kommentar: (Min, Max) är ännu mer lyhörd än (R, Q) eftersom den justerar orderstorleken för att ta hänsyn till hur mycket inventeringen har fallit under Min. När efterfrågan är antingen noll eller en enhet, en gemensam variation sätter Min = Max -1; detta kallas ” base stock policy.”

ett annat policyval: vad händer om jag lagrar ut?

som du kan föreställa dig kommer varje policy sannolikt att leda till en annan tidssekvens av lagernivåer (se Figur 1 nedan). Det finns en annan faktor som påverkar hur händelser spelar ut över tiden: den policy du väljer för att hantera stockouts. I stort sett finns det två huvudmetoder.

restorder policy :om du lager ut, du hålla reda på ordern och fylla den senare. Enligt denna politik är det förnuftigt att tala om negativ inventering. Den negativa inventeringen representerar antalet restorder som behöver fyllas. Förmodligen får alla kunder som tvingas vänta första dibs när påfyllning anländer. Du kommer sannolikt att ha en restorder policy på objekt som är unika för ditt företag som din kund inte kan köpa någon annanstans.

Förlustpolicy: om du lagrar ut, vänder kunden till en annan källa för att fylla sin beställning. När påfyllning anländer kommer någon ny kund att få de nya enheterna. Lager kan aldrig gå under noll. Välj denna policy för varor som enkelt kan köpas från en konkurrent. Om du inte har det i lager kommer din kund säkert att gå någon annanstans.

rollen för efterfrågeprognoser i lagerstyrning

val av Kontrollparametrar, såsom värdena Min och Max, kräver ingångar från någon form av efterfrågeprognosprocess.

traditionellt har detta inneburit att bestämma sannolikhetsfördelningen för antalet enheter som kommer att krävas över ett fast tidsintervall, antingen ledtiden i (R, Q) och (Min, Max) system eller T + ledtid i (T, S) system. Denna fördelning har antagits vara Normal (den berömda “klockformade kurvan”). Traditionella metoder har utökats där efterfrågefördelningen inte antas vara normal utan någon annan distribution (dvs. Poisson, negativ binomial, etc.)

dessa traditionella metoder har flera brister.

• för det första ignorerar det vanligtvis problemet med undershoot, där efterfrågan sjunker lager Inte bara till omordningspunkten utan under den. Om man antar att ingen underskott leder till överskattningar av servicenivåer och fyllningshastigheter.

• för det andra är sannolikhetsfördelningen av efterfrågan Mycket ofta inte ens nära “klockformad” eller vad som helst antagen fördelning valdes-särskilt för artiklar med intermittent efterfrågan som reservdelar och servicedelar.

• för det tredje kräver exakta uppskattningar av lager driftskostnader analys av hela påfyllningscykeln (från en påfyllning till nästa), inte bara den del av cykeln som börjar med inventering som träffar omordningspunkten.

• slutligen, påfyllning ledtider är typiskt oförutsägbara eller slumpmässiga, inte fast. Många modeller antar en fast ledtid baserad på en genomsnittlig, leverantör citerad ledtid eller genomsnittlig ledtid + säkerhetstid.

lyckligtvis finns det bättre lagerplanering och lageroptimeringsprogramvara baserat på att generera ett komplett utbud av slumpmässiga efterfrågescenarier, tillsammans med slumpmässiga ledtider. Dessa scenarier “stresstest” alla föreslagna par parametrar lagerstyrning och bedöma deras förväntade prestanda. Användare kan inte bara välja mellan policyer (dvs. Min, Max vs. R, Q) men också bestämma vilken variation av den föreslagna politiken är bäst (dvs Min, Max 10,20 vs. 15, 25, etc.) Exempel på dessa scenarier ges nedan.

processen att beställa påfyllningslager är tillräckligt dyr och besvärlig att du också vill minimera antalet inköpsorder du måste generera

välja bland lagerkontrollpolicyer

vilken policy är rätt för dig? Det finns en tydlig hackningsordning när det gäller artikeltillgänglighet, med (Min, Max) första, (R, Q) andra och (T, s) sista. Denna ordning härrör från Politikens lyhördhet för fluktuationer i slumpmässigheten i efterfrågan och påfyllning. Ordern vänder när man överväger enkel implementering.

Hur gör du “poäng” resultatet av en lagerpolicy? Det finns två motsatta krafter som måste balanseras: kostnad och service.

lagerkostnad kan uttryckas antingen som lagerinvesteringar eller lager driftskostnad. Den förstnämnda är dollarvärdet för de objekt som väntar på att användas. Den senare är summan av tre komponenter: innehavskostnad (kostnaden för “vård och utfodring av saker på hyllan”), beställningskostnad (i princip kostnaden för att skära en inköpsorder och ta emot den ordern) och bristkostnad (straffet du betalar när du antingen förlorar en försäljning eller tvingar en kund att vänta på vad de vill).

tjänsten mäts vanligtvis med servicenivå och fyllningshastighet. Servicenivå är sannolikheten att ett objekt som begärs skickas omedelbart från lager. Fyllningshastighet är andelen enheter som krävs som skickas omedelbart från lager. Som tidigare professor tänker jag på servicenivån som en allt-eller-ingenting-betyg: om en kund behöver 10 enheter och du bara kan ge 9, är det en F. fyllningsgrad är en partiell kreditbetyg: 9 av 10 är 90%.

när du bestämmer dig för värdena för lagerstyrningspolicyer, hittar du en balans mellan kostnad och service. Du kan ge perfekt service genom att hålla en oändlig inventering. Du kan hålla kostnaderna till noll genom att hålla ingen inventering. Du måste hitta en förnuftig plats att arbeta mellan dessa två löjliga ytterligheter. Generera och analysera efterfrågan scenarier kan kvantifiera konsekvenserna av dina val.

en demonstration av skillnaderna mellan två lagerstyrningspolicyer

vi visar nu hur lager på plats utvecklas annorlunda under två policyer. De två policyerna är (R, Q) och (Min, Max) med restorders tillåtna. För att hålla jämförelsen rättvis ställer vi in Min = r och Max = R+Q, använder en fast ledtid på fem dagar och utsätter båda policyerna för samma sekvens av dagliga krav över 365 simulerade driftsdagar.

Figur 1 visar daglig inventering enligt de två policyerna som utsätts för samma mönster av daglig efterfrågan. I det här exemplet har policyn (Min, Max) endast två perioder med negativ inventering under året, medan policyn (R, Q) har tre. Policyn (Min, Max) fungerar också med ett mindre genomsnittligt antal enheter till hands. Olika efterfrågesekvenser kommer att ge olika resultat, men i allmänhet fungerar (Min, Max) – politiken bättre.

Observera att tomterna i lager på sidan innehåller information som behövs för att beräkna både kostnads-och tillgänglighetsmått.

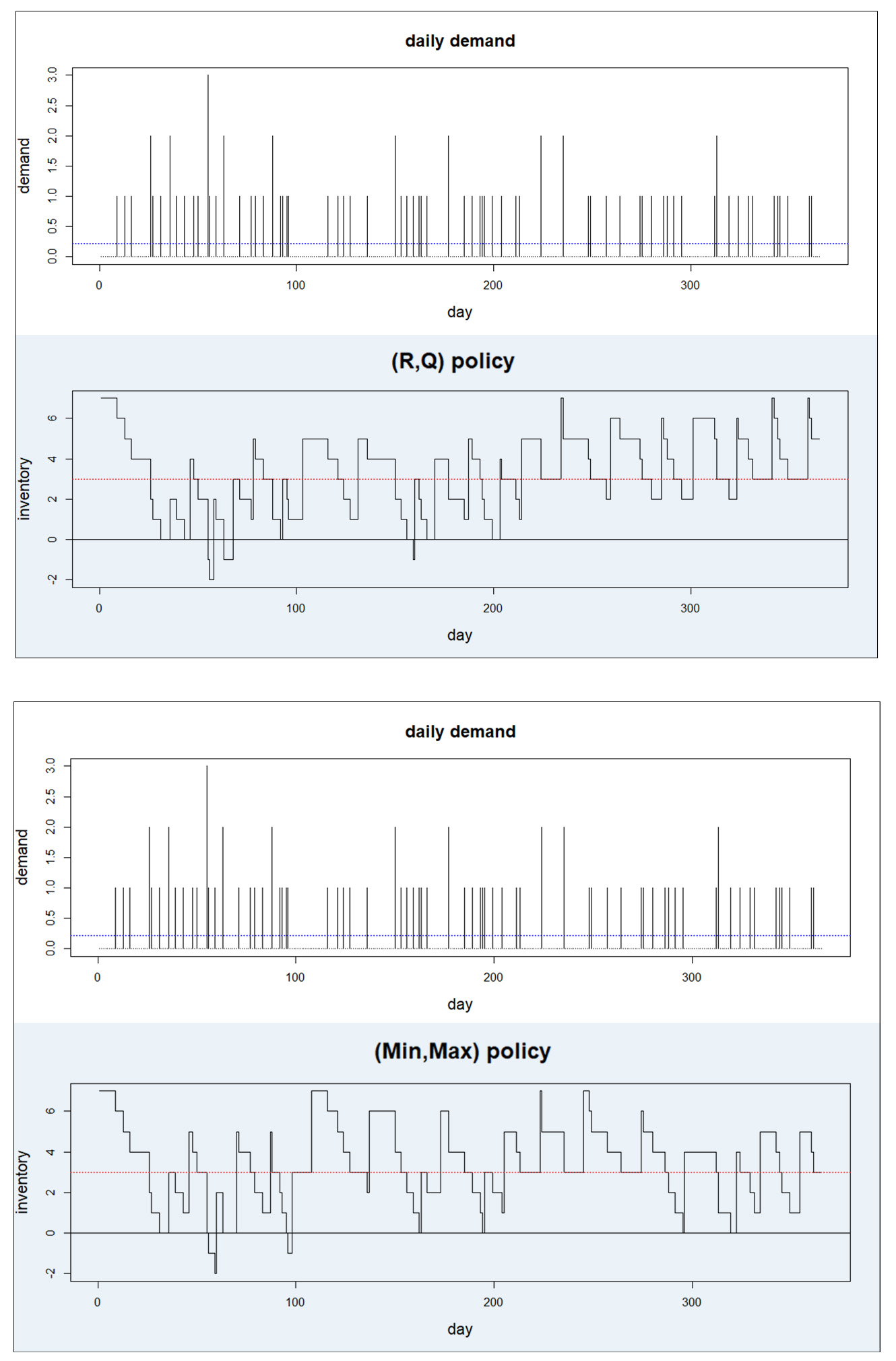
Figur 1: Jämförelse av daglig inventering under två lagerpolicyer

roll av Lagerplaneringsprogramvara

bästa av rasens lagerplanering, prognoser och optimeringssystem kan hjälpa dig att bestämma vilken typ av policy (är det bättre att använda Min/Max över R, Q) och vilka uppsättningar ingångar är optimala (dvs. vad ska jag ange för Min och Max). Best of breed inventory planning and demand forecasting systems kan hjälpa dig att utveckla dessa optimerade ingångar så att du regelbundet kan fylla i och uppdatera dina ERP-system med exakta påfyllningsdrivrutiner.

sammanfattning

vi definierade och beskrev de tre vanligaste lagerstyrningspolicyerna: (T, S), (R, Q) och (Min, Max), tillsammans med de två vanligaste svaren på stockouts: restorders eller lost orders. Vi noterade att denna politik kräver successivt större ansträngningar för att genomföra men också har successivt bättre genomsnittliga resultat. Vi lyfte fram efterfrågeprognosernas roll vid bedömningen av lagerstyrningspolitiken. Slutligen illustrerade vi hur valet av politik påverkar den dagliga nivån på inventeringen.