Univerzitní fyzika svazek 1
8 potenciální energie a úspora energie
cíle učení
na konci této části budete moci:
- charakterizujte konzervativní sílu několika různými způsoby
- specifikujte matematické podmínky, které musí být splněny konzervativní silou a jejími složkami
- vztahujte konzervativní sílu mezi částicemi systému k potenciální energii systému
- Vypočítejte složky konzervativní síly v různých případech
v potenciální energii a zachování energie, jakýkoli přechod mezi kinetickou a potenciální energií zachoval celkovou energii systému. To byla cesta nezávislá, což znamená, že můžeme začít a zastavit v jakýchkoli dvou bodech problému a celková energie systému-kinetická plus potenciál-v těchto bodech jsou si navzájem rovny. To je charakteristické pro konzervativní sílu. V předchozí části jsme se zabývali konzervativními silami, jako je gravitační síla a síla pružiny. Při porovnání pohybu fotbalu v (Obrázek) se celková energie systému nikdy nezmění, i když gravitační potenciální energie fotbalu se zvyšuje, protože míč stoupá vzhledem k zemi a klesá zpět k počáteční gravitační potenciální energii, když fotbalista chytí míč. Nekonzervativní síly jsou disipativní síly, jako je tření nebo odpor vzduchu. Tyto síly odebírají energii ze systému, jak systém postupuje, energii, kterou nemůžete získat zpět. Tyto síly jsou závislé na cestě; proto záleží na tom, kde objekt začíná a končí.
konzervativní síla
práce vykonaná konzervativní silou je nezávislá na cestě; jinými slovy, práce vykonaná konzervativní silou je stejná pro jakoukoli cestu spojující dva body:
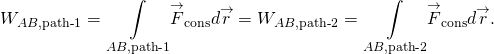
práce nekonzervativní síly závisí na zvolené cestě.
ekvivalentně, síla je konzervativní, pokud práce, kterou dělá kolem jakékoli uzavřené cesty, je nulová:
![]()
(obrázek) a (obrázek) jsou ekvivalentní, protože každá uzavřená cesta je součtem dvou cest: první jde Z A do B, a druhý jde z B do a. práce provedená podél cesty z B do A je negativní práce provedené podél stejné cesty z A do B, kde A A B jsou jakékoli dva body na uzavřené cestě:
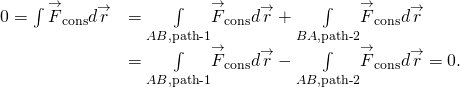
můžete se zeptat, jak jdeme o prokazování, zda síla je konzervativní, protože definice zahrnují všechny cesty od A do B, nebo všechny uzavřené cesty, ale udělat integrál pro práci, musíte si vybrat konkrétní cestu. Jednou z odpovědí je, že vykonaná práce je nezávislá na cestě, pokud nekonečně malá práce
![]()
je přesný diferenciál, způsob, jakým byla nekonečně malá čistá práce rovna přesnému diferenciálu kinetické energie,
![]()
když jsme odvodili větu práce-energie v teorému práce-energie. Existují matematické podmínky, které můžete použít k testování, zda nekonečně malá práce prováděná silou je přesný diferenciál a síla je konzervativní. Tyto podmínky zahrnují pouze diferenciaci, a proto jsou relativně snadno použitelné. Ve dvou rozměrech je podmínka pro
![]()
být přesný rozdíl je
![]()
možná si vzpomenete, že práce vykonaná silou v (Obrázek) závisela na cestě. Pro tuto sílu,
![]()
proto,
![]()
což naznačuje, že jde o nekonzervativní sílu. Vidíte, co byste mohli změnit, aby se z ní stala konzervativní síla?

příklad
konzervativní nebo ne?
která z následujících dvourozměrných sil je konzervativní a která ne? Předpokládejme, že A A b jsou konstanty s příslušnými jednotkami:
(a)
![]()
(b)
![]()
(c)
![]()
strategie
použijte podmínku uvedenou v (obrázek), a to pomocí derivátů složek každé uvedené síly. Pokud je derivace y-složky síly vzhledem k x rovna derivaci x-složky síly vzhledem k y, síla je konzervativní síla, což znamená, že cesta pro potenciální energii nebo pracovní výpočty vždy přináší stejné výsledky.
řešení
-
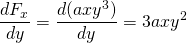
a
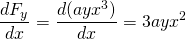
, tato síla je tedy nekonzervativní.
-
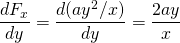
a
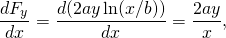
takže tato síla je konzervativní.
-
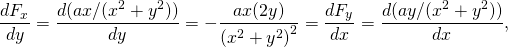
opět konzervativní.
význam
podmínky v (Obrázek) jsou deriváty jako funkce jedné proměnné; ve třech rozměrech existují podobné podmínky, které zahrnují více derivátů.
Zkontrolujte své porozumění
dvourozměrná konzervativní síla je nulová na osách x a y a splňuje podmínku
![]()
. Jaká je velikost síly v bodě
![]()
Zobrazit řešení
2.83 N
než opustíme tuto sekci, poznamenáváme, že nekonzervativní síly nemají s nimi spojenou potenciální energii, protože energie je ztracena v systému a nemůže být později přeměněna na užitečnou práci. Takže vždy existuje konzervativní síla spojená s každou potenciální energií. Viděli jsme, že potenciální energie je definována ve vztahu k práci konzervativních sil. Tento vztah (obrázek) zahrnoval integrál pro práci; počínaje silou a posunem, integrovali jste se, abyste získali práci a změnu potenciální energie. Integrace je však inverzní operací diferenciace; mohli byste stejně dobře začít s potenciální energií a vzít její derivaci s ohledem na posunutí, abyste získali sílu. Infinitezimální přírůstek potenciální energie je bodový součin síly a infinitezimální posunutí,
![]()
zde jsme se rozhodli reprezentovat posun v libovolném směru
![]()
aby nebyla omezena na konkrétní směr souřadnic. Také jsme vyjádřili bodový produkt z hlediska velikosti nekonečně malého posunu a složky síly v jeho směru. Obě tyto veličiny jsou skaláry, takže můžete vydělit dl, abyste získali
![]()
tato rovnice udává vztah mezi silou a potenciální energií s ní spojenou. Slovy, složka konzervativní síly v určitém směru se rovná negativu derivátu odpovídající potenciální energie s ohledem na posun v tomto směru. Pro jednorozměrný pohyb, řekněme podél osy x, (obrázek) dejte celou vektorovou sílu,
![]()
ve dvou rozměrech,
![]()
z této rovnice můžete vidět, proč (obrázek) je podmínkou pro to, aby práce byla přesným diferenciálem, pokud jde o derivace složek síly. Obecně se používá parciální derivační notace. Pokud má funkce v sobě mnoho proměnných, derivace se bere pouze z proměnné, kterou parciální derivace určuje. Ostatní proměnné jsou konstantní. Ve třech rozměrech přidáte další výraz pro z-složku a výsledkem je, že síla je záporná gradientu potenciální energie. Na trojrozměrné příklady se však zatím nebudeme dívat.
příklad
síla působící na Kvartickou potenciální energii
potenciální energie pro částici procházející jednorozměrným pohybem podél osy x je
![]()
kde
![]()
jeho celková energie na
![]()
a nepodléhá žádným nekonzervativním silám. Najděte (a) polohy, kde je jeho kinetická energie nulová, a (b) síly v těchto polohách.
strategie
(a) můžeme najít pozice, kde
![]()
potenciální energie se tedy rovná celkové energii daného systému. (b) pomocí (obrázek) můžeme najít sílu vyhodnocenou v polohách nalezených z předchozí části, protože mechanická energie je zachována.
řešení
- celková energie systému 2 J se rovná kvartické elastické energii, jak je uvedeno v problému,

řešení pro
výsledky v
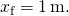
- od (obrázek),
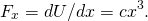
hodnocení síly na
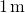
, dostaneme
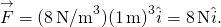
v obou polohách je velikost sil 8 N a směry směřují k původu, protože to je potenciál energie pro obnovení síly.
význam
nalezení síly z potenciální energie je matematicky jednodušší než nalezení potenciální energie ze síly, protože diferenciace funkce je obecně jednodušší než integrace.
Zkontrolujte své porozumění
Najděte síly na částici v (obrázek), když je její kinetická energie 1.0 V
![]()
Zobrazit řešení
![]()
směřuje k původu
shrnutí
- konzervativní síla je síla, pro kterou je vykonaná práce nezávislá na cestě. Ekvivalentně, síla je konzervativní, pokud je práce vykonaná na jakékoli uzavřené cestě nulová.
- nekonzervativní síla je síla, pro kterou práce závisí na cestě.
- pro konzervativní sílu je nekonečná práce přesným diferenciálem. To znamená podmínky pro deriváty složek síly.
- složka konzervativní síly v určitém směru se rovná záporu derivace potenciální energie pro tuto sílu s ohledem na posun v tomto směru.
koncepční otázky
jaký je fyzický význam nekonzervativní síly?
Zobrazit řešení
síla, která odebírá energii ze systému, kterou nelze obnovit, pokud bychom akci zvrátili.
láhev raketa je vystřelena přímo do vzduchu s rychlostí
![]()
. Pokud je odpor vzduchu ignorován, láhev by stoupala do výšky přibližně
![]()
. Raketa však stoupá pouze na
![]()
před návratem na zem. Co se stalo? Vysvětlete a poskytněte pouze kvalitativní odpověď.
vnější síla působí na částici během cesty z jednoho bodu do druhého a zpět do stejného bodu. Tato částice je prováděna pouze konzervativními silami. Mění se kinetická energie a potenciální energie této částice v důsledku této cesty?
Zobrazit řešení
změna kinetické energie je čistá práce. Protože konzervativní síly jsou nezávislé na cestě, když se vrátíte do stejného bodu, kinetické a potenciální energie jsou přesně stejné jako začátek. Během cesty je zachována celková energie, ale mění se potenciální i kinetická energie.
problémy
síla
![]()
působí na částici, jak se pohybuje podél kladné osy x. (a) kolik práce dělá síla na částici, když se pohybuje od
![]()
k
![]()
(b) výběr vhodného referenčního bodu potenciální energie na nulu
![]()
najděte potenciální energii pro tuto sílu.
síla
![]()
působí na částici. (a) kolik práce dělá síla na částici, když se pohybuje od
![]()
k
![]()
(b) výběr vhodného referenčního bodu potenciální energie na nulu
![]()
najděte potenciální energii pro tuto sílu.
Zobrazit řešení
![]()
najděte sílu odpovídající potenciální energii
![]()
funkce potenciální energie pro jeden ze dvou atomů v diatomické molekule je často aproximována
![]()
kde x je vzdálenost mezi atomy. a) v jaké vzdálenosti má potenciální energie lokální minimum (ne na
![]()
(b) jaká je síla na atom při této separaci? c) Jak se síla mění s oddělovací vzdáleností?
Zobrazit řešení
a.
![]()
; b.
![]()
; c.
![]()
částice hmoty
![]()
pohybuje se pod vlivem síly
![]()
pokud je jeho rychlost na
![]()
je
![]()
jaká je jeho rychlost
![]()
částice hmoty
![]()
pohybuje se pod vlivem síly
![]()
pokud je jeho rychlost na
![]()
je
![]()
jaká je jeho rychlost
![]()
Zobrazit řešení
![]()
přepravka na válcích je tlačena bez třecí ztráty energie přes podlahu nákladního automobilu (viz následující obrázek). Auto se pohybuje doprava konstantní rychlostí
![]()
pokud bedna začíná v klidu vzhledem k nákladnímu vozu, pak z věty o pracovní energii,
![]()
kde d, vzdálenost, kterou se přepravka pohybuje, a v, Rychlost přepravky, se měří vzhledem k nákladnímu vozu. a) pozorovateli v klidu vedle kolejí, jakou vzdálenost
![]()
je přepravka tlačena, když pohybuje vzdáleností d v autě? (b) jaké jsou počáteční a konečné rychlosti přepravky
![]()
a
![]()
měřeno pozorovatelem vedle kolejí? c) prokázat, že
![]()
a v důsledku toho se tato práce rovná změně kinetické energie v obou referenčních systémech.
Glosář
konzervativní síla, která funguje nezávisle na cestě přesný diferenciál je celkový diferenciál funkce a vyžaduje použití parciálních derivátů, pokud funkce zahrnuje více než jednu dimenzi nekonzervativní síla síly, která funguje, která závisí na cestě
Leave a Reply