Universitetsfysik Volumen 1
8 potentiel energi og bevarelse af energi
læringsmål
ved udgangen af dette afsnit vil du være i stand til at:
- karakterisere en konservativ kraft på flere forskellige måder
- Angiv matematiske betingelser, der skal opfyldes af en konservativ kraft og dens komponenter
- relatere den konservative kraft mellem partikler i et system til systemets potentielle energi
- Beregn komponenterne i en konservativ kraft i forskellige tilfælde
i potentiel energi og bevarelse af energi bevarede enhver overgang mellem kinetisk og potentiel energi systemets samlede energi. Dette var sti uafhængig, hvilket betyder, at vi kan starte og stoppe på to punkter i problemet, og den samlede energi af systemet—kinetic plus potentiale—på disse punkter er lig med hinanden. Dette er karakteristisk for en konservativ kraft. Vi behandlede konservative kræfter i det foregående afsnit, såsom tyngdekraften og fjederkraften. Når man sammenligner fodboldens bevægelse i (figur), ændres systemets samlede energi aldrig, selvom fodboldens tyngdepotentielle energi øges, da bolden stiger i forhold til jorden og falder tilbage til den oprindelige tyngdepotentielle energi, når fodboldspilleren fanger bolden. Ikke-konservative kræfter er dissipative kræfter såsom friktion eller luftmodstand. Disse kræfter tager energi væk fra systemet, når systemet skrider frem, energi, som du ikke kan få tilbage. Disse kræfter er stiafhængige; derfor betyder det noget, hvor objektet starter og stopper.
konservativ kraft
arbejdet udført af en konservativ styrke er uafhængigt af stien; med andre ord er arbejdet udført af en konservativ styrke det samme for enhver sti, der forbinder to punkter:
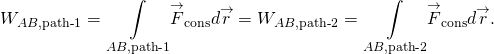
arbejdet udført af en ikke-konservativ styrke afhænger af den vej, der er taget.
tilsvarende er en kraft konservativ, hvis det arbejde, den udfører omkring en lukket sti, er nul:
![]()
(figur) og (figur) er ækvivalente, fordi enhver lukket sti er summen af to stier: den første går fra A til B, og den anden går fra B til A. arbejdet, der udføres ad en sti fra B til A, er det negative ved det udførte arbejde, der går langs den samme sti fra A til B, hvor A og B er to punkter på den lukkede sti:
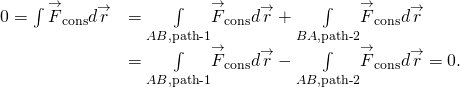
du kan spørge, hvordan vi går om at bevise, om en kraft er konservativ eller ej, da definitionerne involverer alle stier fra A til B eller alle lukkede stier, men for at gøre integralet til arbejdet skal du vælge en bestemt sti. Et svar er, at det udførte arbejde er uafhængigt af stien, hvis det uendelige arbejde
![]()
er en nøjagtig forskel, den måde, hvorpå det uendelige netarbejde var lig med den nøjagtige forskel på den kinetiske energi,
![]()
da vi afledte arbejdsenergisætningen i Arbejdsenergisætningen. Der er matematiske forhold, som du kan bruge til at teste, om det uendelige arbejde, der udføres af en kraft, er en nøjagtig forskel, og kraften er konservativ. Disse betingelser involverer kun differentiering og er således relativt lette at anvende. I to dimensioner er betingelsen for
![]()
at være en nøjagtig forskel er
![]()
du kan huske, at arbejdet udført af kraften i (figur) afhang af stien. For den kraft,
![]()
derfor,
![]()
hvilket indikerer, at det er en ikke-konservativ styrke. Kan du se, hvad du kan ændre for at gøre det til en konservativ styrke?

eksempel
konservativ eller ej?
hvilke af følgende todimensionale kræfter er konservative, og hvilke er det ikke? Antag A og b er konstanter med passende enheder:
(a)
![]()
(b)
![]()
(c)
![]()
strategi
Anvend betingelsen angivet i (figur), nemlig ved hjælp af derivaterne af komponenterne i hver angivet kraft. Hvis derivatet af Y-komponenten af kraften i forhold til Y er lig med derivatet af kraftens komponent i forhold til y, er kraften en konservativ kraft, hvilket betyder, at stien, der tages for potentiel energi eller arbejdsberegninger, altid giver de samme resultater.
opløsning
-
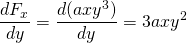
og
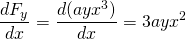
, så denne styrke er ikke-konservativ.
-
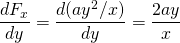
og
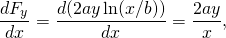
så denne styrke er konservativ.
-
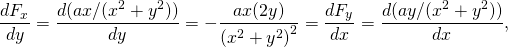
igen konservativ.
Betydning
betingelserne i (figur) er derivater som funktioner af en enkelt variabel; i tre dimensioner findes der lignende betingelser, der involverer flere derivater.
Tjek din forståelse
en todimensionel, konservativ kraft er nul på H-og y-akserne og opfylder betingelsen
![]()
. Hvad er størrelsen af kraften på det punkt
![]()
Vis opløsning
2, 83 N
før vi forlader dette afsnit, bemærker vi, at ikke-konservative kræfter ikke har potentiel energi forbundet med dem, fordi energien går tabt i systemet og ikke kan omdannes til nyttigt arbejde senere. Så der er altid en konservativ kraft forbundet med enhver potentiel energi. Vi har set, at potentiel energi defineres i forhold til det arbejde, der udføres af konservative kræfter. Denne relation (figur) involverede en integreret del af arbejdet; startende med kraften og forskydningen integrerede du for at få arbejdet og ændringen i potentiel energi. Imidlertid er integration den omvendte funktion af differentiering; du kunne lige så godt have startet med den potentielle energi og taget dens derivat med hensyn til forskydning for at få kraften. Den uendelige stigning i potentiel energi er kraftens prikprodukt og den uendelige forskydning,
![]()
her valgte vi at repræsentere forskydningen i en vilkårlig retning ved
![]()
for ikke at være begrænset til nogen bestemt koordinatretning. Vi udtrykte også dot-produktet med hensyn til størrelsen af den uendelige forskydning og komponenten af kraften i dens retning. Begge disse mængder er skalarer, så du kan dividere med dl for at få
![]()
denne ligning giver forholdet mellem kraft og den potentielle energi, der er forbundet med den. I ord er komponenten af en konservativ kraft i en bestemt retning lig med det negative af derivatet af den tilsvarende potentielle energi med hensyn til en forskydning i den retning. For endimensionel bevægelse, sig langs h-aksen, (figur) giv hele vektorkraften,
![]()
i to dimensioner,
![]()
fra denne ligning kan du se, hvorfor (figur) er betingelsen for, at arbejdet skal være en nøjagtig forskel, hvad angår derivaterne af kraftens komponenter. Generelt anvendes en delvis afledt notation. Hvis en funktion har mange variabler i sig, tages derivatet kun af variablen, som det delvise derivat angiver. De andre variabler holdes konstant. I tre dimensioner tilføjer du et andet udtryk for å-komponenten, og resultatet er, at kraften er den negative af gradienten af den potentielle energi. Vi vil dog ikke se på tredimensionelle eksempler endnu.
eksempel
kraft på grund af en Kvartisk potentiel energi
den potentielle energi for en partikel, der gennemgår en-dimensionel bevægelse langs h-aksen, er
![]()
hvor
![]()
dens samlede energi på
![]()
og det er ikke underlagt nogen ikke-konservative kræfter. Find (a) de positioner, hvor dens kinetiske energi er nul, og (b) kræfterne i disse positioner.
strategi
(A) Vi kan finde de positioner, hvor
![]()
så den potentielle energi svarer til den samlede energi i det givne system. (B) ved hjælp af (figur) kan vi finde den kraft, der evalueres på de positioner, der findes fra den foregående del, da den mekaniske energi bevares.
løsning
- systemets samlede energi på 2 J svarer til den kvartiske elastiske energi som angivet i problemet,

løsning for
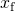
resultater i
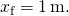
- fra (Figur),
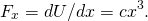
således vurderer styrken ved
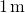
, vi får
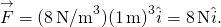
i begge positioner er styrkenes størrelse 8 N, og retningerne er mod oprindelsen, da dette er potentialet energi til en genoprettende kraft.
Betydning
at finde kraften fra den potentielle energi er matematisk lettere end at finde den potentielle energi fra kraften, fordi differentiering af en funktion generelt er lettere end at integrere en.
Tjek din forståelse
Find kræfterne på partiklen i (figur), når dens kinetiske energi er 1.0 J at
![]()
Vis løsning
![]()
rettet mod oprindelsen
Resume
- en konservativ kraft er en, for hvilken det udførte arbejde er uafhængigt af STI. Tilsvarende er en kraft konservativ, hvis arbejdet udført over en lukket sti er nul.
- en ikke-konservativ kraft er en, for hvilken arbejdet afhænger af stien.
- for en konservativ kraft er det uendelige arbejde en nøjagtig forskel. Dette indebærer betingelser for derivaterne af kraftens komponenter.
- komponenten af en konservativ kraft i en bestemt retning er lig med det negative af derivatet af den potentielle energi for den kraft med hensyn til en forskydning i den retning.
konceptuelle spørgsmål
Hvad er den fysiske betydning af en ikke-konservativ kraft?
Vis løsning
en kraft, der tager energi væk fra systemet, der ikke kan gendannes, hvis vi skulle vende handlingen.
en flaske raket er skudt lige op i luften med en hastighed
![]()
. Hvis luftmodstanden ignoreres, flasken ville gå op til en højde på ca
![]()
. Raketten går dog kun op til
![]()
før du vender tilbage til jorden. Hvad skete der? Forklar, giver kun et kvalitativt svar.
en ekstern kraft virker på en partikel under en tur fra et punkt til et andet og tilbage til det samme punkt. Denne partikel udføres kun af konservative kræfter. Ændrer denne partikels kinetiske energi og potentielle energi som følge af denne rejse?
Vis løsning
ændringen i kinetisk energi er nettoarbejdet. Da konservative kræfter er stiuafhængige, når du er tilbage til det samme punkt, er de kinetiske og potentielle energier nøjagtigt de samme som begyndelsen. Under rejsen bevares den samlede energi, men både den potentielle og kinetiske energi ændres.
problemer
en kraft
![]()
virker på en partikel, når den bevæger sig langs den positive h-akse. (a) Hvor meget arbejde gør kraften på partiklen, når den bevæger sig fra
![]()
til
![]()
(B) at vælge et praktisk referencepunkt for den potentielle energi til at være nul ved
![]()
find den potentielle energi til denne kraft.
en kraft
![]()
virker på en partikel. (a) Hvor meget arbejde gør kraften på partiklen, når den bevæger sig fra
![]()
til
![]()
(B) at vælge et praktisk referencepunkt for den potentielle energi til at være nul ved
![]()
find den potentielle energi til denne kraft.
Vis løsning
![]()
Find den kraft, der svarer til den potentielle energi
![]()
den potentielle energifunktion for et af de to atomer i et diatomisk molekyle tilnærmes ofte af
![]()
hvor er afstanden mellem atomerne. (A) på hvilken afstand af adskillelse har den potentielle energi et lokalt minimum (ikke ved
![]()
(b) Hvad er kraften på et atom ved denne adskillelse? (c) hvordan varierer kraften med adskillelsesafstanden?
Vis opløsning
a.
![]()
; b.
![]()
; c.
![]()
en partikel af masse
![]()
bevæger sig under kraftens indflydelse
![]()
hvis dens hastighed ved
![]()
er
![]()
hvad er dens hastighed ved
![]()
en partikel af masse
![]()
bevæger sig under kraftens indflydelse
![]()
hvis dens hastighed ved
![]()
er
![]()
hvad er dens hastighed ved
![]()
Vis løsning
![]()
en kasse på ruller skubbes uden friktionstab af energi over gulvet i en godsvogn (se følgende figur). Bilen bevæger sig til højre med en konstant hastighed
![]()
hvis kassen starter i ro i forhold til godsvognen, så fra arbejdsenergiens sætning,
![]()
hvor d, afstanden kassen bevæger sig, og v, kassens hastighed, måles begge i forhold til godsvognen. (A) til en observatør i hvile ved siden af sporene, hvilken afstand
![]()
skubbes kassen, når den bevæger afstanden d i bilen? (B) Hvad er kassens indledende og endelige hastigheder
![]()
og
![]()
som målt af observatøren ved siden af sporene? C) vise, at
![]()
og derfor er dette arbejde lig med ændringen i kinetisk energi i begge referencesystemer.

ordliste
konservativ kraftkraft, der fungerer uafhængigt af STI nøjagtig forskel er den samlede forskel for en funktion og kræver brug af partielle derivater, hvis funktionen involverer mere end en dimension ikke-konservativ kraftkraft, der fungerer, der afhænger af STI
Leave a Reply