Universitätsphysik Band 1
8 Potenzielle Energie und Energieeinsparung
Lernziele
Am Ende dieses Abschnitts können Sie:
- Charakterisieren Sie eine konservative Kraft auf verschiedene Arten
- Geben Sie mathematische Bedingungen an, die von einer konservativen Kraft und ihren Komponenten erfüllt sein müssen
- Beziehen Sie die konservative Kraft zwischen Teilchen eines Systems auf die potentielle Energie des Systems
- Berechnen Sie die Komponenten einer konservativen Kraft
Bei der potentiellen Energie und Energieeinsparung konservierte jeder Übergang zwischen kinetischer und potentieller Energie die Gesamtenergie des Systems. Dies war pfadunabhängig, was bedeutet, dass wir an zwei beliebigen Punkten des Problems starten und stoppen können und die Gesamtenergie des Systems — Kinetik plus Potential — an diesen Punkten gleich ist. Dies ist charakteristisch für eine konservative Kraft. Wir haben uns im vorhergehenden Abschnitt mit konservativen Kräften wie der Schwerkraft und der Federkraft befasst. Beim Vergleich der Bewegung des Fußballs in (Abbildung) ändert sich die Gesamtenergie des Systems nie, obwohl die potentielle Gravitationsenergie des Fußballs zunimmt, wenn der Ball relativ zum Boden ansteigt und auf die anfängliche potentielle Gravitationsenergie zurückfällt, wenn der Fußballspieler den Ball fängt. Nichtkonservative Kräfte sind dissipative Kräfte wie Reibung oder Luftwiderstand. Diese Kräfte nehmen dem System Energie weg, während das System fortschreitet, Energie, die Sie nicht zurückbekommen können. Diese Kräfte sind pfadabhängig; Daher kommt es darauf an, wo das Objekt beginnt und stoppt.
Konservative Kraft
Die Arbeit einer konservativen Kraft ist unabhängig vom Pfad; mit anderen Worten, die Arbeit einer konservativen Kraft ist für jeden Pfad, der zwei Punkte verbindet, gleich:
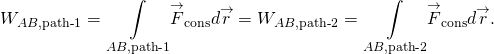
Die Arbeit einer nicht konservativen Kraft hängt vom eingeschlagenen Weg ab.
Äquivalent ist eine Kraft konservativ, wenn die Arbeit, die sie um einen geschlossenen Pfad ausführt, Null ist:
![]()
( Abbildung) und (Abbildung) sind äquivalent, da jeder geschlossene Pfad die Summe zweier Pfade ist: die erste geht von A nach B und die zweite von B nach A. Die geleistete Arbeit auf einem Pfad von B nach A ist das Negativ der geleisteten Arbeit auf demselben Pfad von A nach B, wobei A und B zwei beliebige Punkte auf dem geschlossenen Pfad sind:
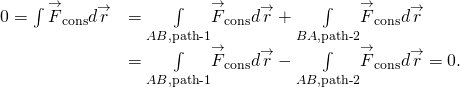
Sie könnten fragen, wie wir beweisen, ob eine Kraft konservativ ist oder nicht, da die Definitionen alle Pfade von A nach B oder alle geschlossenen Pfade beinhalten, aber um das Integral für die Arbeit zu tun, müssen Sie einen bestimmten Pfad wählen. Eine Antwort ist, dass die geleistete Arbeit unabhängig vom Pfad ist, wenn die infinitesimale Arbeit
![]()
ist ein exaktes Differential, die Art und Weise, wie das infinitesimale Netz gleich dem exakten Differential der kinetischen Energie war,
![]()
wenn wir den Arbeitsenergiesatz im Arbeitsenergiesatz abgeleitet haben. Es gibt mathematische Bedingungen, mit denen Sie testen können, ob die infinitesimale Arbeit einer Kraft ein genaues Differential ist und die Kraft konservativ ist. Diese Bedingungen beinhalten nur eine Differenzierung und sind daher relativ einfach anzuwenden. In zwei Dimensionen, die Bedingung für
![]()
um ein genaues Differential zu sein, ist
![]()
Sie erinnern sich vielleicht, dass die Arbeit der Kraft in (Abbildung) vom Pfad abhing. Für diese Kraft,
![]()
Daher,
![]()
was darauf hindeutet, dass es sich um eine nicht konservative Kraft handelt. Können Sie sehen, was Sie ändern könnten, um es zu einer konservativen Kraft zu machen?

Beispiel
Konservativ oder nicht?
Welche der folgenden zweidimensionalen Kräfte sind konservativ und welche nicht? Angenommen, a und b sind Konstanten mit entsprechenden Einheiten:
(a)
![]()
( b)
![]()
( c)
![]()
Strategie
Wenden Sie die in (Abbildung) angegebene Bedingung an, nämlich unter Verwendung der Ableitungen der Komponenten jeder angegebenen Kraft. Wenn die Ableitung der y-Komponente der Kraft in Bezug auf x gleich der Ableitung der x-Komponente der Kraft in Bezug auf y ist, ist die Kraft eine konservative Kraft, was bedeutet, dass der Weg, der für potentielle Energie- oder Arbeitsberechnungen genommen wird, immer die gleichen Ergebnisse liefert.
Lösung
-
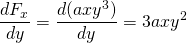
und
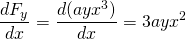
, diese Kraft ist also nicht konservativ.
-
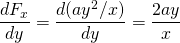
und
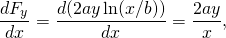
diese Kraft ist also konservativ.
-
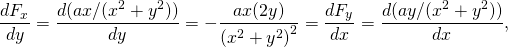
wieder konservativ.
Signifikanz
Die Bedingungen in (Abbildung) sind Ableitungen als Funktionen einer einzelnen Variablen; In drei Dimensionen existieren ähnliche Bedingungen, die mehr Ableitungen beinhalten.
Überprüfen Sie Ihr Verständnis
Eine zweidimensionale, konservative Kraft ist auf der x– und y-Achse Null und erfüllt die Bedingung
![]()
. Was ist die Größe der Kraft an dem Punkt
![]()
Lösung anzeigen
2,83 N
Bevor wir diesen Abschnitt verlassen, stellen wir fest, dass nichtkonservativen Kräften keine potentielle Energie zugeordnet ist, da die Energie für das System verloren geht und später nicht in nützliche Arbeit umgewandelt werden kann. Mit jeder potentiellen Energie ist also immer eine konservative Kraft verbunden. Wir haben gesehen, dass potentielle Energie in Bezug auf die Arbeit konservativer Kräfte definiert wird. Diese Beziehung (Abbildung) beinhaltete ein Integral für die Arbeit; Beginnend mit der Kraft und der Verschiebung müssen Sie die Arbeit und die Änderung der potentiellen Energie erhalten. Integration ist jedoch die umgekehrte Operation der Differenzierung; Sie hätten genauso gut mit der potentiellen Energie beginnen und ihre Ableitung in Bezug auf die Verschiebung nehmen können, um die Kraft zu erhalten. Das infinitesimale Inkrement der potentiellen Energie ist das Punktprodukt der Kraft und der infinitesimalen Verschiebung,
![]()
Hier haben wir uns entschieden, die Verschiebung in eine beliebige Richtung darzustellen, indem wir
![]()
um nicht auf eine bestimmte Koordinatenrichtung beschränkt zu sein. Wir haben das Punktprodukt auch in Bezug auf die Größe der infinitesimalen Verschiebung und die Komponente der Kraft in ihrer Richtung ausgedrückt. Beide Größen sind Skalare, so dass Sie durch dl dividieren können, um zu erhalten
![]()
Diese Gleichung gibt die Beziehung zwischen Kraft und der damit verbundenen potentiellen Energie an. Mit anderen Worten, die Komponente einer konservativen Kraft in einer bestimmten Richtung ist gleich dem Negativ der Ableitung der entsprechenden potentiellen Energie in Bezug auf eine Verschiebung in dieser Richtung. Für eine eindimensionale Bewegung, sagen wir entlang der x-Achse, (Abbildung) geben Sie die gesamte Vektorkraft an,
![]()
In zwei Dimensionen,
![]()
Aus dieser Gleichung können Sie sehen, warum (Abbildung) die Bedingung für die Arbeit ist, ein genaues Differential zu sein, in Bezug auf die Ableitungen der Komponenten der Kraft. Im Allgemeinen wird eine partielle Ableitungsnotation verwendet. Wenn eine Funktion viele Variablen enthält, wird die Ableitung nur von der Variablen genommen, die die partielle Ableitung angibt. Die anderen Variablen werden konstant gehalten. In drei Dimensionen fügen Sie einen weiteren Begriff für die Z-Komponente hinzu, und das Ergebnis ist, dass die Kraft das Negative des Gradienten der potentiellen Energie ist. Wir werden uns jedoch noch keine dreidimensionalen Beispiele ansehen.
Beispiel
Kraft aufgrund einer quartischen potentiellen Energie
Die potentielle Energie für ein Teilchen, das sich entlang der x-Achse eindimensional bewegt, beträgt
![]()
wo
![]()
Seine Gesamtenergie bei
![]()
und es unterliegt keinen nicht-konservativen Kräften. Finden Sie (a) die Positionen, an denen seine kinetische Energie Null ist, und (b) die Kräfte an diesen Positionen.
Strategie
(a) Wir können die Positionen finden, an denen
![]()
die potentielle Energie entspricht also der Gesamtenergie des gegebenen Systems. (b) Mit (Abbildung) können wir die an den Positionen des vorherigen Teils ausgewertete Kraft ermitteln, da die mechanische Energie erhalten bleibt.
Lösung
- Die Gesamtenergie des Systems von 2 J entspricht der im Problem angegebenen quartischen elastischen Energie,

Lösung für
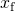
ergebnisse in
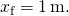
- Von (Abbildung),
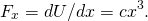
Somit wird die Bewertung der Kraft bei
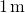
, wir bekommen
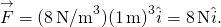
An beiden Positionen beträgt die Größe der Kräfte 8 N und die Richtungen sind zum Ursprung gerichtet, da dies das Potential ist energie für eine Rückstellkraft.
Bedeutung
Das Finden der Kraft aus der potentiellen Energie ist mathematisch einfacher als das Finden der potentiellen Energie aus der Kraft, da das Differenzieren einer Funktion im Allgemeinen einfacher ist als das Integrieren einer Funktion.
Überprüfen Sie Ihr Verständnis
Finden Sie die Kräfte auf das Teilchen in (Abbildung), wenn seine kinetische Energie 1 ist.0 J bei
![]()
Lösung anzeigen
![]()
auf den Ursprung gerichtet
Zusammenfassung
- Eine konservative Kraft ist eine, für die die geleistete Arbeit unabhängig vom Pfad ist. Äquivalent ist eine Kraft konservativ, wenn die über einen geschlossenen Pfad geleistete Arbeit Null ist.
- Eine nichtkonservative Kraft ist eine Kraft, deren geleistete Arbeit vom Pfad abhängt.
- Für eine konservative Kraft ist die infinitesimale Arbeit ein genaues Differential. Dies impliziert Bedingungen für die Ableitungen der Komponenten der Kraft.
- Die Komponente einer konservativen Kraft in einer bestimmten Richtung ist gleich dem Negativ der Ableitung der potentiellen Energie für diese Kraft in Bezug auf eine Verschiebung in dieser Richtung.
Konzeptionelle Fragen
Was ist die physikalische Bedeutung einer nicht-konservativen Kraft?
Lösung anzeigen
Eine Kraft, die dem System Energie entzieht, die nicht zurückgewonnen werden kann, wenn wir die Aktion umkehren.
Eine Flaschenrakete wird mit einer Geschwindigkeit direkt in die Luft geschossen
![]()
. Wenn der Luftwiderstand ignoriert wird, würde die Flasche bis zu einer Höhe von ungefähr gehen
![]()
. Allerdings geht die Rakete bis zu nur
![]()
vor der Rückkehr auf den Boden. Was passierte? Erklären Sie, geben Sie nur eine qualitative Antwort.
Eine äußere Kraft wirkt auf ein Teilchen während einer Reise von einem Punkt zum anderen und zurück zu demselben Punkt. Dieses Teilchen wird nur durch konservative Kräfte bewirkt. Ändert sich die kinetische Energie und die potentielle Energie dieses Teilchens infolge dieser Reise?
Lösung anzeigen
Die Änderung der kinetischen Energie ist das Netzwerk. Da konservative Kräfte pfadunabhängig sind, sind die kinetischen und potentiellen Energien genau die gleichen wie am Anfang, wenn Sie wieder am selben Punkt sind. Während der Fahrt bleibt die Gesamtenergie erhalten, aber sowohl die potentielle als auch die kinetische Energie ändern sich.
Probleme
Eine Kraft
![]()
wirkt auf ein Teilchen, wenn es sich entlang der positiven x-Achse bewegt. (a) Wie viel Arbeit leistet die Kraft auf das Teilchen, wenn es sich von
![]()
zu
![]()
( b) Auswahl eines geeigneten Bezugspunkts der potentiellen Energie, um bei Null zu sein
![]()
finde die potentielle Energie für diese Kraft.
Eine Kraft
![]()
wirkt auf ein Teilchen. (a) Wie viel Arbeit leistet die Kraft auf das Teilchen, wenn es sich von
![]()
zu
![]()
( b) Auswahl eines geeigneten Bezugspunkts der potentiellen Energie, um bei Null zu sein
![]()
finde die potentielle Energie für diese Kraft.
Lösung anzeigen
![]()
Finde die Kraft, die der potentiellen Energie entspricht
![]()
Die potentielle Energiefunktion für eines der beiden Atome in einem zweiatomigen Molekül wird oft angenähert durch
![]()
wobei x der Abstand zwischen den Atomen ist. (a) In welchem Abstand der Trennung hat die potentielle Energie ein lokales Minimum (nicht bei
![]()
( b) Was ist die Kraft auf ein Atom bei dieser Trennung? (c) Wie ändert sich die Kraft mit dem Abstand?
Lösung anzeigen
a.
![]()
; b.
![]()
; c.
![]()
Ein Teilchen der Masse
![]()
bewegt sich unter dem Einfluss der Kraft
![]()
Wenn seine Geschwindigkeit bei
![]()
ist
![]()
was ist seine Geschwindigkeit bei
![]()
Ein Teilchen der Masse
![]()
bewegt sich unter dem Einfluss der Kraft
![]()
Wenn seine Geschwindigkeit bei
![]()
ist
![]()
was ist seine Geschwindigkeit bei
![]()
Lösung anzeigen
![]()
Eine Kiste auf Rollen wird ohne Kraftverlust über den Boden eines Güterwagens geschoben (siehe folgende Abbildung). Das Auto bewegt sich mit konstanter Geschwindigkeit nach rechts
![]()
Wenn die Kiste relativ zum Güterwagen in Ruhe beginnt, dann aus dem Arbeitsenergiesatz,
![]()
wobei d, der Abstand, den die Kiste bewegt, und v, die Geschwindigkeit der Kiste, beide relativ zum Güterwagen gemessen werden. (a) Zu einem Beobachter in Ruhe neben den Gleisen, welche Entfernung
![]()
wird die Kiste geschoben, wenn sie sich im Auto um die Strecke d bewegt? (b) Was sind die Anfangs- und Endgeschwindigkeiten der Kiste
![]()
und
![]()
wie vom Beobachter neben den Gleisen gemessen? c) Zeigen, dass
![]()
und folglich ist diese Arbeit gleich der Änderung der kinetischen Energie in beiden Bezugssystemen.
Glossar
konservative Kraft Kraft, die pfadunabhängig arbeitet exaktes Differential ist das Gesamtdifferential einer Funktion und erfordert die Verwendung partieller Ableitungen, wenn die Funktion mehr als eine Dimension umfasst nichtkonservative Kraft Kraft, die pfadunabhängig arbeitet
Leave a Reply