yliopiston fysiikka Volume 1
8 potentiaalienergia ja energian säästö
oppimistavoitteet
tämän jakson loppuun mennessä voit:
- luonnehtii konservatiivista voimaa useilla eri tavoilla
- Määritä matemaattiset ehdot, jotka konservatiivisen voiman on täytettävä ja sen komponentit
- suhteuta systeemin hiukkasten välinen konservatiivinen voima systeemin potentiaalienergiaan
- laske konservatiivisen voiman komponentit eri tapauksissa
Potentiaalienergiassa ja energian säilymisessä kaikki siirtymät kineettisen ja potentiaalienergian välillä säilyttivät systeemin kokonaisenergian. Tämä oli polusta riippumaton, mikä tarkoittaa, että voimme aloittaa ja pysähtyä missä tahansa ongelman kahdessa pisteessä, ja systeemin kokonaisenergia—kineettinen plus potentiaali—näissä pisteissä ovat yhtä suuret keskenään. Tämä on tyypillistä konservatiiviselle voimalle. Käsittelimme edellisessä osassa konservatiivisia voimia, kuten painovoimaa ja jousivoimaa. Verrattaessa jalkapallon liikettä (Kuva), systeemin kokonaisenergia ei koskaan muutu, vaikka jalkapallon gravitaatiopotentiaalienergia kasvaa, koska pallo nousee suhteessa maahan ja putoaa takaisin alkuperäiseen gravitaatiopotentiaalienergiaan, kun jalkapalloilija nappaa pallon. Ei-konservatiiviset voimat ovat hajottavia voimia, kuten kitkaa tai ilmanvastusta. Nämä voimat vievät järjestelmän edetessä energiaa, jota ei voi saada takaisin. Nämä voimat ovat polkuriippuvaisia, joten sillä on merkitystä, mistä kappale alkaa ja pysähtyy.
konservatiivinen voima
konservatiivisen voiman tekemä työ on polusta riippumaton; toisin sanoen konservatiivisen voiman tekemä työ on sama mille tahansa kahta pistettä yhdistävälle polulle:
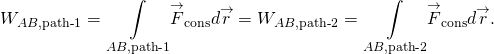
ei-konservatiivisen voiman tekemä työ riippuu siitä, mihin suuntaan mennään.
vastaavasti voima on konservatiivinen, jos sen minkä tahansa suljetun polun ympärillä tekemä työ on nolla:
![]()
(kuva) ja (kuva) ovat ekvivalentteja, koska mikä tahansa suljettu polku on kahden polun summa: ensimmäinen menee A: sta B: hen ja toinen menee B: stä A: han. tehty työ, joka kulkee polkua B: stä A: han, on negatiivinen työ, joka kulkee samaa polkua A: sta B: hen, missä A ja B ovat mikä tahansa kaksi pistettä suljetulla polulla:
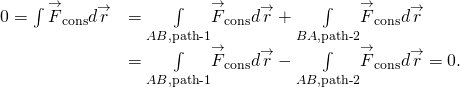
saatat kysyä, miten me mennä noin todistaa, onko voima on konservatiivinen, koska määritelmät sisältävät kaikki polut A: sta B: hen, tai kaikki ja kaikki suljetut polut, mutta tehdä olennainen työ, sinun täytyy valita tietty polku. Yksi vastaus on, että tehty työ on polusta riippumaton, jos äärettömän pieni työ
![]()
on tarkka differentiaali, miten äärettömän pieni nettotyö oli yhtä suuri kuin kineettisen energian eksaktinen differentiaali,
![]()
kun johdimme työenergialauseen Työenergialauseeseen. On olemassa matemaattisia ehtoja, joiden avulla voidaan testata, onko voiman tekemä äärettömän pieni työ tarkka differentiaali, ja voima on konservatiivinen. Näihin ehtoihin sisältyy vain eriyttämistä, joten niitä on suhteellisen helppo soveltaa. Kahdessa ulottuvuudessa edellytyksenä
![]()
olla tarkka ero on
![]()
saatat muistaa, että työn voima (Kuva) riippui polusta. For that force,
![]()
siksi,
![]()
mikä osoittaa, että se on ei-konservatiivinen voima. Näetkö, mitä voisit muuttaa tehdäksesi siitä konservatiivisen voiman?

esimerkki
konservatiivinen vai ei?
Mitkä seuraavista kaksiulotteisista joukoista ovat konservatiivisia ja mitkä eivät? Oletetaan, että a ja b ovat vakioita, joilla on asianmukaiset yksiköt:
(a)
![]()
(b)
![]()
(c)
![]()
strategia
sovelletaan (kuvassa) esitettyä ehtoa, nimittäin käyttämällä kunkin ilmoitetun voiman komponenttien johdannaisia. Jos voiman y-komponentin derivaatta suhteessa x: ään on yhtä suuri kuin voiman x-komponentin derivaatta suhteessa y: hen, voima on konservatiivinen voima, eli potentiaalienergia-tai työlaskelmiin valittu polku tuottaa aina samat tulokset.
liuos
-
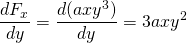
ja
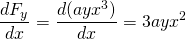
, tämä voima ei siis ole konservatiivinen.
-
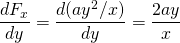
ja
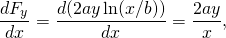
tämä voima on siis konservatiivinen.
-
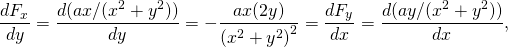
jälleen konservatiivinen.
merkitsevyys
(Kuvan) ehdot ovat derivaatat yhden muuttujan funktioina; kolmessa ulottuvuudessa esiintyy samanlaisia ehtoja, jotka sisältävät useampia derivaattoja.
Tarkista ymmärryksesi
kaksiulotteinen, konservatiivinen voima on nolla x-ja y-akseleilla, ja täyttää ehdon
![]()
. Mikä on voiman suuruus pisteessä
![]()
Näytä liuos
2, 83 N
ennen kuin poistumme tästä osiosta, huomaamme, että ei-konservatiivisilla voimilla ei ole niihin liittyvää potentiaalienergiaa, koska energia katoaa systeemiin eikä sitä voida myöhemmin muuttaa hyödylliseksi työksi. Jokaiseen potentiaalienergiaan liittyy siis aina konservatiivinen voima. Olemme nähneet, että potentiaalienergia määritellään suhteessa konservatiivisten voimien tekemään työhön. Tämä suhde, (kuva), mukana integraali työtä; alkaen voima ja siirtymä, olet integroitu saada työtä ja muutos potentiaalienergian. Integraatio on kuitenkin erilaistumisen käänteistä toimintaa; yhtä hyvin olisi voinut aloittaa potentiaalienergiasta ja ottaa sen derivaatan, suhteessa siirtymiseen, voiman saamiseksi. Potentiaalienergian infinitesimaalinen lisäys on voiman ja infinitesimaalisen siirtymän pistetulo,
![]()
täällä päätimme edustaa Siirtymä mielivaltaiseen suuntaan
![]()
jotta se ei rajoittuisi mihinkään tiettyyn koordinointisuuntaan. Ilmaisimme myös pistetulon infinitesimaalisen siirtymän suuruuden ja sen suuntaisen voiman komponentin suhteen. Molemmat määrät ovat skalaareja, joten voit jakaa dl saada
![]()
tämä yhtälö antaa voiman ja siihen liittyvän potentiaalienergian suhteen. Sanalla sanoen konservatiivisen voiman komponentti tietyssä suunnassa on yhtä suuri kuin vastaavan potentiaalienergian derivaatan negatiivinen suhteessa siirtymiseen tähän suuntaan. Yksiulotteisessa liikkeessä sanotaan X-akselin suuntaisesti, (kuva) annetaan koko vektorivoima,
![]()
kahdessa ulottuvuudessa,
![]()
tästä yhtälöstä voit nähdä, miksi (Kuva) on ehto sille, että työ on tarkka differentiaali, mitä tulee voiman komponenttien johdannaisiin. Yleensä käytetään osittaisderivaattamerkintää. Jos funktiossa on useita muuttujia, derivaatta otetaan vain siitä muuttujasta, jonka osittaisderivaatta määrittelee. Muut muuttujat pysyvät vakiona. Kolmessa ulottuvuudessa Z-komponentille lisätään toinen termi, ja tuloksena on, että voima on potentiaalienergian gradientin negatiivinen. Emme kuitenkaan katso vielä kolmiulotteisia esimerkkejä.
esimerkki
Kvartisen potentiaalienergian aiheuttama voima
yksiulotteisen liikkeen x-akselilla käyvän hiukkasen potentiaalienergia on
![]()
jossa
![]()
sen kokonaisenergia at
![]()
eikä siihen kohdistu mitään ei-konservatiivisia voimia. Etsi (a) kannat, joissa sen kineettinen energia on nolla ja (b) voimat näissä asemissa.
strategia
(a) voimme löytää paikat, joissa
![]()
potentiaalienergia on siis yhtä suuri kuin annetun systeemin kokonaisenergia. (B) käyttämällä (kuva), voimme löytää voima arvioidaan kantoja löytyy edellisestä osasta, koska mekaaninen energia on säilytetty.
ratkaisu
- systeemin kokonaisenergia 2 J on yhtä suuri kuin ongelmassa annettu kvarttinen kimmoenergia,

Solving for
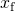
tulokset
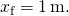
- alkaen (Kuva),
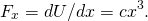
näin arvioidaan voimassa
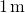
, saamme
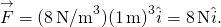
molemmissa kohdissa voimien magnitudi on 8 N ja suunnat ovat kohti alkuperää, koska tämä on potentiaali energiaa palauttavaan voimaan.
merkitsevyys
voiman löytäminen potentiaalienergiasta on matemaattisesti helpompaa kuin potentiaalienergian löytäminen voimasta, koska funktion differentioiminen on yleensä helpompaa kuin yhden integroiminen.
Tarkista ymmärryksesi
Etsi voimia hiukkasen (Kuva), kun sen kineettinen energia on 1.0 J
![]()
Näytä ratkaisu
![]()
suunnattu kohti alkuperää
Yhteenveto
- konservatiivinen voima on sellainen, jolle tehty työ on polusta riippumaton. Vastaavasti voima on konservatiivinen, jos minkä tahansa suljetun polun yli tehty työ on nolla.
- Ei-Konservatiivinen voima on sellainen, jolle tehty työ riippuu polusta.
- konservatiiviselle voimalle äärettömän pieni teos on tarkka differentiaali. Tämä merkitsee ehtoja voiman komponenttien johdannaisille.
- konservatiivisen voiman komponentti tietyssä suunnassa on yhtä suuri kuin kyseisen voiman potentiaalienergian derivaatta negatiivinen suhteessa siirtymiseen tähän suuntaan.
käsitteelliset kysymykset
mikä on ei-konservatiivisen voiman fyysinen merkitys?
Näytä ratkaisu
voima, joka vie energiaa pois systeemistä, jota ei voida ottaa takaisin, jos kumoaisimme toiminnan.
pulloraketti ammutaan suoraan ilmaan vauhdilla
![]()
. Jos ilmanvastusta ei huomioida, pullo nousisi noin korkeaksi
![]()
. Raketti nousee kuitenkin vain
![]()
ennen paluutaan maahan. Mitä kävi? Selitä, antaa vain laadullisen vastauksen.
ulkoinen voima vaikuttaa hiukkaseen matkan aikana pisteestä toiseen ja takaisin samaan pisteeseen. Tätä hiukkasta saavat aikaan vain konservatiiviset voimat. Muuttuuko hiukkasen liike-energia ja potentiaalienergia tämän matkan seurauksena?
Näytä ratkaisu
liike-energian muutos on nettotyö. Koska konservatiiviset voimat ovat polusta riippumattomia, palatessasi samaan pisteeseen kineettiset ja potentiaaliset energiat ovat täsmälleen samat kuin alussa. Matkan aikana kokonaisenergia säilyy, mutta sekä potentiaali-että liike-energia muuttuvat.
ongelmat
voima
![]()
vaikuttaa hiukkaseen sen liikkuessa positiivista X-akselia pitkin. (a) Kuinka paljon työtä tekee voima tehdä hiukkanen kun se siirtyy
![]()
voit
![]()
(b) Poiminta kätevä viittaus pisteen potentiaalienergia olisi nolla
![]()
löytää potentiaalienergia tämä voima.
voima
![]()
vaikuttaa hiukkaseen. (a) Kuinka paljon työtä tekee voima tehdä hiukkanen kun se siirtyy
![]()
voit
![]()
(b) Poiminta kätevä viittaus pisteen potentiaalienergia olisi nolla
![]()
löytää potentiaalienergia tämä voima.
Näytä ratkaisu
![]()
Etsi voima, joka vastaa potentiaalienergiaa
![]()
diatomisen molekyylin jommankumman atomin potentiaalienergiafunktiota approksimoidaan usein
![]()
missä x on atomien välinen etäisyys. (a) millä etäisyydellä erotuksesta potentiaalienergialla on paikallinen minimi (Ei at
![]()
(b) mikä on atomiin kohdistuva voima tässä erossa? c) miten voima vaihtelee erotusetäisyyden mukaan?
Näytä liuos
a.
![]()
; b.
![]()
; n.
![]()
massahiukkanen
![]()
liikkuu voiman vaikutuksen alaisena
![]()
jos sen nopeus
![]()
on
![]()
mikä on sen nopeus
![]()
massahiukkanen
![]()
liikkuu voiman vaikutuksen alaisena
![]()
jos sen nopeus
![]()
m
![]()
mikä on sen nopeus
![]()
Näytä ratkaisu
![]()
rullissa olevaa laatikkoa työnnetään ilman kitkaista energiahäviötä tavaravaunun lattian poikki (katso seuraava kuva). Auto siirtyy oikealle vakionopeudella
![]()
jos laatikko alkaa levossa suhteessa tavaravaunuun, niin työenergialauseesta,
![]()
missä D, Etäisyys laatikon liikkuu, ja v, nopeus laatikon, molemmat mitataan suhteessa tavaravaunu. (a) tarkkailijalle levossa raiteiden vieressä, mikä etäisyys
![]()
työnnetäänkö laatikkoa, kun se liikkuu matkan d autossa? (B) mitkä ovat laatikon alku-ja loppunopeudet
![]()
ja
![]()
mitattuna raiteiden vieressä olevan tarkkailijan avulla? (C) Näytä, että
![]()
ja näin ollen tämä työ on yhtä suuri kuin liike-energian muutos molemmissa vertailujärjestelmissä.
Sanasto
konservatiivinen voimavoima, joka toimii polkutarkasta differentiaalista riippumatta, on funktion kokonaisdifferentiaali ja vaatii osittaisderivaatan käyttöä, jos funktioon liittyy useampi kuin yksi ulottuvuus ei-konservatiivinen voimavoima, joka toimii polusta riippuvana
Leave a Reply