Volume de Physique Universitaire 1
8 Énergie potentielle et Conservation de l’énergie
Objectifs d’apprentissage
À la fin de cette section, vous pourrez ::
- Caractériser une force conservatrice de plusieurs manières différentes
- Spécifier les conditions mathématiques qui doivent être satisfaites par une force conservatrice et ses composantes
- Relier la force conservatrice entre les particules d’un système à l’énergie potentielle du système
- Calculer les composantes d’une force conservatrice dans divers cas
Dans l’énergie potentielle et la conservation de l’énergie, toute transition entre l’énergie cinétique et l’énergie potentielle conservait l’énergie totale du système. C’était indépendant du chemin, ce qui signifie que nous pouvons commencer et nous arrêter à deux points quelconques du problème, et l’énergie totale du système — cinétique plus potentiel — à ces points sont égales l’une à l’autre. Ceci est caractéristique d’une force conservatrice. Nous avons traité des forces conservatrices dans la section précédente, telles que la force gravitationnelle et la force du ressort. En comparant le mouvement du football dans (Figure), l’énergie totale du système ne change jamais, même si l’énergie potentielle gravitationnelle du football augmente, car la balle monte par rapport au sol et retombe à l’énergie potentielle gravitationnelle initiale lorsque le joueur de football attrape la balle. Les forces non conservatrices sont des forces dissipatives telles que le frottement ou la résistance à l’air. Ces forces enlèvent de l’énergie au système à mesure que le système progresse, énergie que vous ne pouvez pas récupérer. Ces forces dépendent du chemin; il importe donc où l’objet commence et s’arrête.
Force conservatrice
Le travail effectué par une force conservatrice est indépendant du chemin; en d’autres termes, le travail effectué par une force conservatrice est le même pour tout chemin reliant deux points:
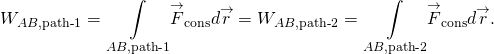
Le travail effectué par une force non conservatrice dépend du chemin emprunté.
De manière équivalente, une force est conservatrice si le travail qu’elle effectue autour d’un chemin fermé est nul:
![]()
( Figure) et (Figure) sont équivalentes car tout chemin fermé est la somme de deux chemins: le premier va de A à B, et le second va de B à A. Le travail effectué suivant un chemin de B à A est le négatif du travail effectué suivant le même chemin de A à B, où A et B sont deux points quelconques sur le chemin fermé:
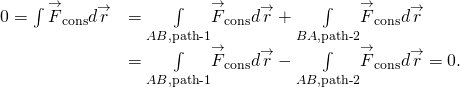
Vous pourriez vous demander comment nous allons prouver si une force est conservatrice ou non, puisque les définitions impliquent tous les chemins de A à B, ou tous les chemins fermés, mais pour faire l’intégrale pour le travail, vous devez choisir un chemin particulier. Une réponse est que le travail effectué est indépendant du chemin si le travail infinitésimal
![]()
est un différentiel exact, la façon dont le travail net infinitésimal était égal au différentiel exact de l’énergie cinétique,
![]()
lorsque nous avons dérivé le théorème de l’énergie de travail dans le Théorème de l’énergie de travail. Il existe des conditions mathématiques que vous pouvez utiliser pour tester si le travail infinitésimal effectué par une force est un différentiel exact, et la force est conservatrice. Ces conditions n’impliquent qu’une différenciation et sont donc relativement faciles à appliquer. En deux dimensions, la condition pour
![]()
pour être un différentiel exact est
![]()
Vous vous souvenez peut-être que le travail effectué par la force dans (Figure) dépendait du chemin. Pour cette force,
![]()
Par conséquent,
![]()
ce qui indique qu’il s’agit d’une force non conservatrice. Pouvez-vous voir ce que vous pourriez changer pour en faire une force conservatrice?

Exemple
Conservateur ou non?
Lesquelles des forces bidimensionnelles suivantes sont conservatrices et lesquelles ne le sont pas ? Supposons que a et b sont des constantes avec des unités appropriées:
(d)
![]()
( d)
![]()
( c)
![]()
Stratégie
Appliquer la condition indiquée dans (Figure), à savoir utiliser les dérivées des composantes de chaque force indiquée. Si la dérivée de la composante y de la force par rapport à x est égale à la dérivée de la composante x de la force par rapport à y, la force est une force conservatrice, ce qui signifie que le chemin emprunté pour les calculs d’énergie potentielle ou de travail donne toujours les mêmes résultats.
Solution
-
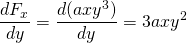
et
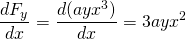
, cette force n’est donc pas conservatrice.
-
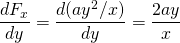
et
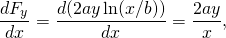
cette force est donc conservatrice.
-
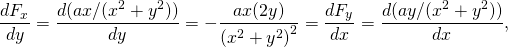
encore une fois conservateur.
Signification
Les conditions de (Figure) sont des dérivées en tant que fonctions d’une seule variable; en trois dimensions, des conditions similaires existent qui impliquent plus de dérivées.
Vérifiez Votre Compréhension
Une force conservatrice bidimensionnelle est nulle sur les axes x et y et satisfait la condition
![]()
. Quelle est l’ampleur de la force au point
![]()
Afficher la solution
2,83 N
Avant de quitter cette section, nous notons que les forces non conservatrices n’ont pas d’énergie potentielle qui leur est associée car l’énergie est perdue pour le système et ne peut pas être transformée en travail utile plus tard. Il y a donc toujours une force conservatrice associée à chaque énergie potentielle. Nous avons vu que l’énergie potentielle est définie par rapport au travail effectué par les forces conservatrices. Cette relation, (Figure), impliquait une intégrale pour le travail; en commençant par la force et le déplacement, vous avez intégré pour obtenir le travail et le changement d’énergie potentielle. Cependant, l’intégration est l’opération inverse de la différenciation; vous auriez tout aussi bien pu commencer avec l’énergie potentielle et prendre sa dérivée, par rapport au déplacement, pour obtenir la force. L’incrément infinitésimal d’énergie potentielle est le produit scalaire de la force et du déplacement infinitésimal,
![]()
Ici, nous avons choisi de représenter le déplacement dans une direction arbitraire par
![]()
afin de ne pas être limité à une direction de coordonnées particulière. Nous avons également exprimé le produit scalaire en termes d’amplitude du déplacement infinitésimal et de la composante de la force dans sa direction. Ces deux quantités sont des scalaires, vous pouvez donc diviser par dl pour obtenir
![]()
Cette équation donne la relation entre la force et l’énergie potentielle qui lui est associée. En termes, la composante d’une force conservatrice, dans une direction particulière, est égale au négatif de la dérivée de l’énergie potentielle correspondante, par rapport à un déplacement dans cette direction. Pour un mouvement unidimensionnel, disons le long de l’axe des abscisses, (Figure) donne la force vectorielle entière,
![]()
En deux dimensions,
![]()
À partir de cette équation, vous pouvez voir pourquoi (Figure) est la condition pour que le travail soit un différentiel exact, en termes de dérivées des composantes de la force. En général, une notation dérivée partielle est utilisée. Si une fonction contient de nombreuses variables, la dérivée n’est prise que de la variable spécifiée par la dérivée partielle. Les autres variables sont maintenues constantes. En trois dimensions, vous ajoutez un autre terme pour la composante z, et le résultat est que la force est le négatif du gradient de l’énergie potentielle. Cependant, nous ne regarderons pas encore d’exemples en trois dimensions.
Exemple
Force due à une Énergie potentielle quartique
L’énergie potentielle pour une particule subissant un mouvement unidimensionnel le long de l’axe des abscisses est
![]()
où
![]()
Son énergie totale à
![]()
et il n’est soumis à aucune force non conservatrice. Trouvez (a) les positions où son énergie cinétique est nulle et (b) les forces à ces positions.
Stratégie
(a) Nous pouvons trouver les positions où
![]()
l’énergie potentielle est donc égale à l’énergie totale du système donné. (b) En utilisant (Figure), on peut trouver la force évaluée aux positions trouvées dans la partie précédente, puisque l’énergie mécanique est conservée.
Solution
- L’énergie totale du système de 2 J est égale à l’énergie élastique quartique donnée dans le problème,

Résoudre pour
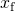
résultats en
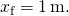
- De (Figure),
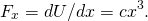
Ainsi, l’évaluation de la force à
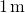
, nous obtenons
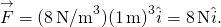
Aux deux positions, l’amplitude des forces est de 8 N et les directions sont vers l’origine, car il s’agit du potentiel énergie pour une force de restauration.
Signification
Trouver la force à partir de l’énergie potentielle est mathématiquement plus facile que de trouver l’énergie potentielle à partir de la force, car différencier une fonction est généralement plus facile que d’en intégrer une.
Vérifiez Votre Compréhension
Trouvez les forces sur la particule dans (Figure) lorsque son énergie cinétique est de 1.0 J au
![]()
Afficher La Solution
![]()
dirigé vers l’origine
Résumé
- Une force conservatrice est une force pour laquelle le travail effectué est indépendant du chemin. De manière équivalente, une force est conservatrice si le travail effectué sur un chemin fermé est nul.
- Une force non conservatrice est une force pour laquelle le travail effectué dépend du chemin.
- Pour une force conservatrice, le travail infinitésimal est un différentiel exact. Cela implique des conditions sur les dérivées des composantes de la force.
- La composante d’une force conservatrice, dans une direction particulière, est égale au négatif de la dérivée de l’énergie potentielle pour cette force, par rapport à un déplacement dans cette direction.
Questions Conceptuelles
Quelle est la signification physique d’une force non conservatrice?
Afficher la solution
Une force qui enlève de l’énergie au système qui ne peut pas être récupérée si nous devions inverser l’action.
Une fusée de bouteille est tirée directement en l’air avec une vitesse
![]()
. Si la résistance à l’air est ignorée, la bouteille atteindrait une hauteur d’environ
![]()
. Cependant, la fusée monte à seulement
![]()
avant de retourner au sol. Qu’est-ce qui s’est passé? Expliquez, en ne donnant qu’une réponse qualitative.
Une force externe agit sur une particule lors d’un voyage d’un point à un autre et de retour à ce même point. Cette particule n’est effectuée que par des forces conservatrices. L’énergie cinétique et l’énergie potentielle de cette particule changent-elles à la suite de ce voyage?
Afficher la solution
Le changement d’énergie cinétique est le travail net. Puisque les forces conservatrices sont indépendantes du chemin, lorsque vous êtes de retour au même point, les énergies cinétique et potentielle sont exactement les mêmes qu’au début. Pendant le voyage, l’énergie totale est conservée, mais l’énergie potentielle et cinétique change.
Problèmes
Une force
![]()
agit sur une particule lorsqu’elle se déplace le long de l’axe des abscisses positives. (a) Combien de travail la force exerce-t-elle sur la particule lorsqu’elle se déplace de
![]()
à
![]()
( b) Choisir un point de référence commode pour que l’énergie potentielle soit nulle à
![]()
trouvez l’énergie potentielle pour cette force.
Une force
![]()
agit sur une particule. (a) Combien de travail la force exerce-t-elle sur la particule lorsqu’elle se déplace de
![]()
à
![]()
( b) Choisir un point de référence commode pour que l’énergie potentielle soit nulle à
![]()
trouvez l’énergie potentielle pour cette force.
Afficher La Solution
![]()
Trouver la force correspondant à l’énergie potentielle
![]()
La fonction d’énergie potentielle pour l’un des deux atomes d’une molécule diatomique est souvent approximée par
![]()
où x est la distance entre les atomes. a) À quelle distance de séparation l’énergie potentielle a-t-elle un minimum local (pas à
![]()
( b) Quelle est la force sur un atome à cette séparation ? c) Comment la force varie-t-elle avec la distance de séparation?
Afficher la solution
a.
![]()
; d.
![]()
; c.
![]()
Une particule de masse
![]()
se déplace sous l’influence de la force
![]()
Si sa vitesse à
![]()
est
![]()
quelle est sa vitesse à
![]()
Une particule de masse
![]()
se déplace sous l’influence de la force
![]()
Si sa vitesse à
![]()
est
![]()
quelle est sa vitesse à
![]()
Afficher La Solution
![]()
Une caisse sur rouleaux est poussée sans perte d’énergie par frottement sur le plancher d’un wagon de marchandises (voir la figure suivante). La voiture se déplace vers la droite avec une vitesse constante
![]()
Si la caisse démarre au repos par rapport au wagon de marchandises, alors à partir du théorème de l’énergie de travail,
![]()
où d, la distance parcourue par la caisse, et v, la vitesse de la caisse, sont toutes deux mesurées par rapport au wagon de marchandises. a) À un observateur au repos près des voies, à quelle distance
![]()
la caisse est-elle poussée lorsqu’elle déplace la distance d dans la voiture? (b) Quelles sont les vitesses initiale et finale de la caisse
![]()
et
![]()
comme mesuré par l’observateur à côté des pistes? c) Montrer que
![]()
et, par conséquent, ce travail est égal au changement d’énergie cinétique dans les deux systèmes de référence.

Glossaire
force conservatrice la force qui fonctionne indépendamment du chemin la différentielle exacte est la différentielle totale d’une fonction et nécessite l’utilisation de dérivées partielles si la fonction implique plus d’une dimension force non conservatrice force qui fonctionne qui dépend du chemin
Leave a Reply