egyetemi fizika kötet 1
8 potenciális energia és energiamegmaradás
tanulási célok
e szakasz végére képes lesz arra, hogy:
- a konzervatív erő jellemzése többféle módon
- adja meg azokat a matematikai feltételeket, amelyeket a konzervatív erőnek és összetevőinek teljesítenie kell
- kapcsolja össze a rendszer részecskéi közötti konzervatív erőt a rendszer potenciális energiájával
- Számítsa ki a konzervatív erő összetevőit különböző esetekben
a potenciális energiában és az Energiamegmaradásban a kinetikus és a potenciális energia közötti átmenet megőrizte a rendszer teljes energiáját. Ez útfüggetlen volt, ami azt jelenti, hogy a probléma bármely két pontján elindulhatunk és megállhatunk, és a rendszer teljes energiája—kinetikus plusz potenciál—ezeken a pontokon egyenlő egymással. Ez egy konzervatív erőre jellemző. Az előző részben a konzervatív erőkkel foglalkoztunk, mint például a gravitációs erő és a rugóerő. A futball mozgásának (ábra) összehasonlításakor a rendszer teljes energiája soha nem változik, annak ellenére, hogy a futball gravitációs potenciális energiája növekszik, amikor a labda a talajhoz képest emelkedik, és visszaesik a kezdeti gravitációs potenciális energiához, amikor a futballista elkapja a labdát. A nem konzervatív erők disszipatív erők, például súrlódás vagy légellenállás. Ezek az erők elveszik az energiát a rendszertől, ahogy a rendszer fejlődik, olyan energiát, amelyet nem tudsz visszaszerezni. Ezek az erők útfüggőek, ezért fontos, hogy az objektum hol kezdődik és hol áll meg.
konzervatív erő
a konzervatív erő által végzett munka független az úttól; más szavakkal, a konzervatív erő által végzett munka ugyanaz minden két pontot összekötő út esetében:
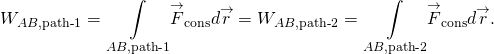
a nem konzervatív erő által végzett munka a megtett úttól függ.
Ekvivalensen egy erő konzervatív, ha bármely zárt út körül végzett munka nulla:
![]()
(Ábra) és (ábra) ekvivalensek, mert bármely zárt út két út összege: az első A-ból B-be, a második pedig B-ből A. A B-ből A-ba vezető út mentén végzett munka negatívja annak a munkának, amely ugyanazon az úton halad A-tól B-ig, ahol A és B a zárt út bármely két pontja:
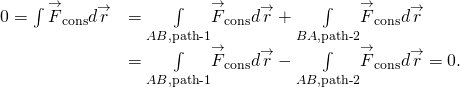
megkérdezheti, hogyan bizonyítjuk, hogy egy erő konzervatív-e vagy sem, mivel a definíciók magukban foglalják az A-tól B-ig terjedő összes utat, vagy az összes zárt utat, de a munka integráljának elvégzéséhez egy adott utat kell választania. Az egyik válasz az, hogy az elvégzett munka független az úttól, ha a végtelenül kis munka
![]()
pontos különbség, ahogyan a végtelenül kis nettó munka megegyezett a kinetikus energia pontos különbségével,
![]()
amikor levezetjük a munka-energia tételt a munka-energia tételben. Vannak matematikai feltételek, amelyek segítségével tesztelheti, hogy az erő által végzett végtelen kis munka pontos differenciál-e, és az erő konzervatív. Ezek a feltételek csak differenciálást jelentenek, ezért viszonylag könnyen alkalmazhatók. Két dimenzióban a feltétel
![]()
ahhoz, hogy pontos különbség legyen, az
![]()
emlékeztethet arra, hogy az erő (ábra) által végzett munka az úttól függött. Erre az erőre,
![]()
ezért,
![]()
ami azt jelzi, hogy nem konzervatív erő. Látod, mit lehetne változtatni, hogy ez egy konzervatív erő?

példa
konzervatív vagy nem?
az alábbi kétdimenziós erők közül melyik konzervatív és melyik nem? Tegyük fel, hogy a és b konstansok megfelelő egységekkel:
(a)
![]()
(b)
![]()
(c)
![]()
stratégia
alkalmazza az (ábrán) megadott feltételt,nevezetesen az egyes jelzett erők összetevőinek származékait. Ha az erő y-komponensének X-hez viszonyított deriváltja megegyezik az erő x-komponensének y-hez viszonyított deriváltjával, akkor az erő konzervatív erő, ami azt jelenti, hogy a potenciális energia vagy a munka számításaihoz megtett út mindig ugyanazokat az eredményeket adja.
megoldás
-
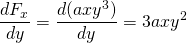
és
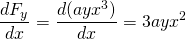
, tehát ez az erő nem konzervatív.
-
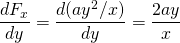
és
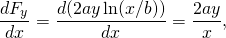
tehát ez az erő konzervatív.
-
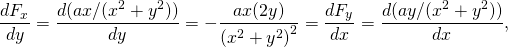
ismét konzervatív.
jelentőség
az (ábra) feltételei származékok, mint egyetlen változó függvényei; három dimenzióban léteznek hasonló feltételek, amelyek több származékot tartalmaznak.
ellenőrizze a megértését
a kétdimenziós, konzervatív erő nulla az x-és y-tengelyen, és kielégíti a feltételt
![]()
. Mekkora az erő nagysága a ponton
![]()
oldat megjelenítése
2,83 N
mielőtt elhagynánk ezt a részt, megjegyezzük, hogy a nem konzervatív erőknek nincs potenciális energiájuk, mert az energia elveszik a rendszer számára, és később nem alakítható hasznos munkává. Tehát mindig van egy konzervatív erő, amely minden potenciális energiához kapcsolódik. Láttuk, hogy a potenciális energiát a konzervatív erők által végzett munkához viszonyítva határozzák meg. Ez a kapcsolat (ábra) magában foglalta a munka integrálját; kezdve az erővel és az elmozdulással, integrálódtál, hogy megkapd a munkát és a potenciális energia változását. Az integráció azonban a differenciálódás fordított művelete; ugyanúgy jól kezdhettük volna a potenciális energiával, és a származékát, az elmozdulás tekintetében, megkaphattuk volna az erőt. A potenciális energia végtelen kis növekedése az erő pontterméke és a végtelen kis elmozdulás,
![]()
itt, úgy döntöttünk, hogy az elmozdulást tetszőleges irányban ábrázoljuk
![]()
annak érdekében, hogy ne korlátozódjon egy adott koordináta-irányra. A dot szorzatot a végtelen kis elmozdulás nagyságával és az erő irányának összetevőjével is kifejeztük. Mindkét mennyiség skalár, így eloszthatja dl-vel, hogy megkapja
![]()
ez az egyenlet adja meg az erő és a hozzá kapcsolódó potenciális energia közötti kapcsolatot. Szavakkal, a konzervatív erő komponense egy adott irányban megegyezik a megfelelő potenciális energia deriváltjának negatívjával, az ebbe az irányba történő elmozdulás tekintetében. Egydimenziós mozgáshoz mondjuk az x tengely mentén (ábra) adja meg a teljes vektorerőt,
![]()
két dimenzióban,
![]()
ebből az egyenletből láthatja, hogy miért (ábra) az a feltétel, hogy a munka pontos különbség legyen, az erő összetevőinek származékai szempontjából. Általában részleges származékos jelölést használnak. Ha egy függvényben sok változó van, akkor a derivált csak a parciális derivált által meghatározott változóból származik. A többi változó állandó. Három dimenzióban hozzáadunk egy másik kifejezést A z-komponenshez, és az eredmény az, hogy az erő a potenciális energia gradiensének negatívja. A háromdimenziós példákat azonban még nem fogjuk megvizsgálni.
példa
kvartikus potenciális energia által okozott erő
az X tengely mentén egydimenziós mozgáson áteső részecske potenciális energiája
![]()
ahol
![]()
a teljes energia
![]()
nem tartozik semmilyen nem konzervatív erő alá. Keresse meg (a) azokat a pozíciókat, ahol mozgási energiája nulla, és (b) az ezen pozíciókban lévő erőket.
stratégia
(a) megtaláljuk azokat a pozíciókat, ahol
![]()
tehát a potenciális energia megegyezik az adott rendszer teljes energiájával. (b) az (ábra) segítségével megtalálhatjuk az előző részből talált pozíciókban értékelt erőt, mivel a mechanikai energia konzerválódik.
megoldás
- a 2 J rendszer teljes energiája megegyezik a problémában megadott kvartikus rugalmas energiával,

megoldás a
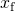
eredmények
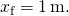
- tól től (ábra),
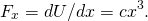
így az erő értékelése a
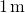
, kapunk
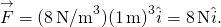
mindkét helyzetben az erők nagysága 8 N, az irányok pedig az eredet felé mutatnak, mivel ez a potenciál energia egy helyreállító erő.
jelentőség
matematikailag könnyebb megtalálni az erőt a potenciális energiából, mint megtalálni a potenciális energiát az erőből, mert egy függvény megkülönböztetése általában könnyebb, mint egy integrálása.
ellenőrizze a megértését
keresse meg a részecskére ható erőket (ábra), ha kinetikus energiája 1.0 J at
![]()
megoldás megjelenítése
![]()
a származás felé irányul
Összegzés
- a konzervatív erő az, amelynél az elvégzett munka független az úttól. Ekvivalensen egy erő konzervatív, ha bármely zárt úton végzett munka nulla.
- a nem konzervatív erő az, amelynél az elvégzett munka az úttól függ.
- egy konzervatív erő esetében a végtelenül kis munka pontos különbség. Ez magában foglalja az erő összetevőinek származékainak feltételeit.
- a konzervatív erő komponense egy adott irányban megegyezik az adott erő potenciális energiájának deriváltjának negatívjával az adott irányú elmozdulás tekintetében.
fogalmi kérdések
mi a nem konzervatív erő fizikai jelentése?
Show Solution
olyan erő, amely energiát vesz el a rendszerből, amelyet nem lehet visszanyerni, ha megfordítjuk a műveletet.
egy palack rakétát sebességgel egyenesen a levegőbe lőnek
![]()
. Ha a légellenállást figyelmen kívül hagyja, a palack körülbelül magasságba emelkedik
![]()
. A rakéta azonban csak
![]()
mielőtt visszatérne a földre. Mi történt? Magyarázza el, csak minőségi választ adva.
egy külső erő hat a részecskére az egyik pontról a másikra való utazás során, majd vissza ugyanabba a pontba. Ezt a részecskét csak konzervatív erők hajtják végre. Változik-e ennek a részecskének a mozgási energiája és potenciális energiája az utazás eredményeként?
megoldás megjelenítése
a kinetikus energia változása a nettó munka. Mivel a konzervatív erők útfüggetlenek, amikor visszatérünk ugyanabba a pontba, a kinetikus és potenciális energiák pontosan ugyanazok, mint a kezdet. Az utazás során a teljes energia megmarad, de mind a potenciális, mind a kinetikus energia megváltozik.
problémák
egy erő
![]()
egy részecskére hat, amikor a pozitív x tengely mentén mozog. (a) mennyi munkát végez az erő a részecskén, amikor mozog
![]()
hogy
![]()
(b) a potenciális energia kényelmes referenciapontjának kiválasztása nulla
![]()
keresse meg ennek az erőnek a potenciális energiáját.
egy erő
![]()
egy részecskére hat. (a) mennyi munkát végez az erő a részecskén, amikor mozog
![]()
hogy
![]()
(b) a potenciális energia kényelmes referenciapontjának kiválasztása nulla
![]()
keresse meg ennek az erőnek a potenciális energiáját.
megoldás megjelenítése
![]()
keresse meg a potenciális energiának megfelelő erőt
![]()
a kétatomos molekula két atomjának bármelyikének potenciális energiafunkcióját gyakran megközelíti
![]()
ahol x az atomok közötti távolság. (a) milyen távolságra van a potenciális energia helyi minimum (nem a
![]()
(b) mekkora erő van egy atomon ebben az elválasztásban? c) hogyan változik az erő az elválasztási távolsággal?
megoldás megjelenítése
a.
![]()
; b.
![]()
; c.
![]()
a tömeg részecske
![]()
az erő hatása alatt mozog
![]()
ha a sebesség
![]()
van
![]()
mi a sebessége
![]()
a tömeg részecske
![]()
az erő hatása alatt mozog
![]()
ha a sebesség
![]()
is
![]()
mi a sebessége
![]()
megoldás megjelenítése
![]()
a görgőkön lévő ládát súrlódási energiaveszteség nélkül tolják át a teherkocsi padlóján (lásd az alábbi ábrát). Az autó állandó sebességgel jobbra mozog
![]()
ha a láda nyugalomban kezdődik a teherkocsihoz képest, akkor a munka-energia tételből,
![]()
ahol d, a láda mozgásának távolsága, és v, a láda sebessége, mind a teherkocsihoz viszonyítva mérjük. (a) A pálya mellett nyugvó megfigyelőnek, milyen távolságra
![]()
a ládát tolják, amikor a D távolságot mozgatja az autóban? (b) mik a láda kezdeti és végső sebességei
![]()
és
![]()
ahogy a megfigyelő a sínek mellett méri? c) mutassa be, hogy
![]()
következésképpen ez a munka megegyezik a kinetikus energia változásával mindkét referenciarendszerben.
szószedet
konzervatív erő az út pontos különbségétől függetlenül működő erő egy függvény teljes különbsége, és parciális deriváltak használatát igényli, ha a függvény egynél több dimenziót tartalmaz nem konzervatív erő erő, amely az úttól függ
Leave a Reply