Volume di fisica universitaria 1
8 Energia potenziale e conservazione dell’energia
Obiettivi formativi
Alla fine di questa sezione, si sarà in grado di:
- Caratterizzare una forza conservatrice in diversi modi
- Specificare matematica condizioni che devono essere soddisfatte da una forza conservatrice e dei suoi componenti
- Riguardano la forza conservatrice tra le particelle di un sistema per l’energia potenziale del sistema
- Calcolare le componenti di una forza conservatrice in vari casi
In Energia Potenziale e Conservazione dell’Energia, transizione tra cinetica e di energia potenziale conservata l’energia totale del sistema. Questo è stato percorso indipendente, il che significa che possiamo iniziare e fermarsi in qualsiasi due punti del problema, e l’energia totale del sistema—cinetica più potenziale—in questi punti sono uguali tra loro. Questo è caratteristico di una forza conservatrice. Abbiamo affrontato le forze conservative nella sezione precedente, come la forza gravitazionale e la forza della molla. Quando si confronta il movimento del calcio in (Figura), l’energia totale del sistema non cambia mai, anche se l’energia potenziale gravitazionale del calcio aumenta, poiché la palla sale rispetto al suolo e ricade all’energia potenziale gravitazionale iniziale quando il giocatore di calcio cattura la palla. Le forze non conservative sono forze dissipative come l’attrito o la resistenza dell’aria. Queste forze portano via energia dal sistema mentre il sistema progredisce, energia che non puoi recuperare. Queste forze dipendono dal percorso; quindi è importante dove l’oggetto inizia e si ferma.
Forza Conservatrice
Il lavoro fatto da una forza conservatrice è indipendente dal percorso; in altre parole, il lavoro compiuto da una forza conservatrice è la stessa per qualsiasi percorso che collega due punti:
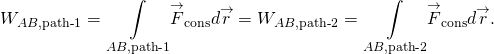
Il lavoro fatto da un non-conservatore forza dipende dal percorso intrapreso.
Equivalentemente, una forza è conservativa se il lavoro che fa attorno a qualsiasi percorso chiuso è zero:
![]()
(Figura) e (Figura) sono equivalenti perché ogni percorso chiuso è la somma di due percorsi: prima di andare da a a B, e la seconda che va da B ad A. Il lavoro svolto percorrendo un sentiero da B ad a è il negativo del lavoro svolto percorrendo lo stesso percorso da a a B, dove A e B sono due punti qualsiasi del tracciato chiuso:
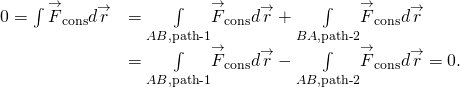
Si potrebbe chiedere come possiamo dimostrare se o non una forza è conservativa, dal momento che le definizioni di coinvolgere qualsiasi e tutti i percorsi da a a B, o qualsiasi e tutti i tracciati chiusi, ma per fare l’integrale per il lavoro, è necessario scegliere un determinato percorso. Una risposta è che il lavoro fatto è indipendente dal percorso, se infinitesimale di lavoro
![]()
è un differenziale esatto, il modo infinitesimale lavoro netto è stato pari al differenziale esatta dell’energia cinetica,
![]()
quando abbiamo derivato il lavoro-energia teorema Lavoro-Energia Teorema. Esistono condizioni matematiche che è possibile utilizzare per verificare se il lavoro infinitesimale svolto da una forza è un differenziale esatto e la forza è conservativa. Queste condizioni comportano solo differenziazione e sono quindi relativamente facili da applicare. In due dimensioni, la condizione per
![]()
per essere un differenziale esatto è
![]()
Si può ricordare che il lavoro svolto dalla forza in (Figura) dipendeva dal percorso. Per quella forza,
![]()
Pertanto,
![]()
il che indica che è una forza non conservatrice. Riesci a vedere cosa potresti cambiare per renderlo una forza conservatrice?

Esempio
Conservatore o no?
Quali delle seguenti forze bidimensionali sono conservative e quali no? Supponiamo che a e b siano costanti con unità appropriate:
(a)
![]()
(b)
![]()
(c)
![]()
Strategia
Applicare la condizione di cui al paragrafo (Figura), vale a dire, utilizzando i derivati dei componenti di ciascuna forza indicata. Se la derivata della componente y della forza rispetto a x è uguale alla derivata della componente x della forza rispetto a y, la forza è una forza conservativa, il che significa che il percorso intrapreso per i calcoli di energia potenziale o di lavoro produce sempre gli stessi risultati.
Soluzione
-
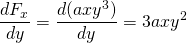
e
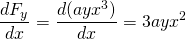
, quindi questa forza non è conservativa.
-
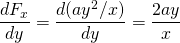
e
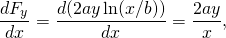
quindi questa forza è conservatrice.
-
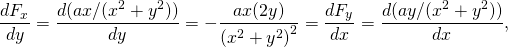
di nuovo conservatore.
Significato
Le condizioni in (Figura) sono derivate come funzioni di una singola variabile; in tre dimensioni, esistono condizioni simili che coinvolgono più derivate.
Controlla la tua comprensione
Una forza bidimensionale e conservativa è zero sugli assi x e y e soddisfa la condizione
![]()
. Che cosa è l’ordine di grandezza della forza di cui al punto
![]()
Soluzione Spettacolo
2.83 N
Prima di lasciare questa sezione, si nota che i non-forze conservative non hanno energia potenziale associata con loro, perché l’energia viene persa dal sistema e non può essere trasformata in lavoro utile in seguito. Quindi c’è sempre una forza conservativa associata ad ogni energia potenziale. Abbiamo visto che l’energia potenziale è definita in relazione al lavoro svolto dalle forze conservatrici. Quella relazione, (Figura), implicava un integrale per il lavoro; partendo dalla forza e dallo spostamento, si integrava per ottenere il lavoro e il cambiamento di energia potenziale. Tuttavia, l’integrazione è l’operazione inversa della differenziazione; si potrebbe ugualmente iniziare con l’energia potenziale e prendere la sua derivata, rispetto allo spostamento, per ottenere la forza. L’incremento infinitesimale dell’energia potenziale è il prodotto dot della forza e dello spostamento infinitesimale,
![]()
Qui, abbiamo scelto di rappresentare lo spostamento in una direzione arbitraria di
![]()
in modo da non essere limitato a una particolare direzione coordinata. Abbiamo anche espresso il prodotto dot in termini di grandezza dello spostamento infinitesimale e della componente della forza nella sua direzione. Entrambe queste quantità sono scalari, quindi puoi dividere per dl per ottenere
![]()
Questa equazione fornisce la relazione tra la forza e l’energia potenziale ad essa associata. In parole, la componente di una forza conservativa, in una particolare direzione, è uguale al negativo della derivata dell’energia potenziale corrispondente, rispetto a uno spostamento in quella direzione. Per uno-dimensionale di movimento, dire lungo l’asse x (Figura) dare l’intero vettore di forza,
![]()
In due dimensioni,
![]()
Da questa equazione si può vedere perché (Figura) è la condizione per il lavoro per essere un differenziale esatta, in termini di derivate delle componenti della forza. In generale, viene utilizzata una notazione derivata parziale. Se una funzione ha molte variabili in essa, la derivata viene presa solo dalla variabile specificata dalla derivata parziale. Le altre variabili sono mantenute costanti. In tre dimensioni, si aggiunge un altro termine per il componente z e il risultato è che la forza è il negativo del gradiente dell’energia potenziale. Tuttavia, non vedremo ancora esempi tridimensionali.
Esempio
Forza a causa di una Quartica Energia Potenziale
L’energia potenziale di una particella in fase uno-dimensionale moto lungo l’asse x è
![]()
dove
![]()
la Sua energia totale al
![]()
e non è soggetto a qualsiasi non-forze conservative. Trova (a) le posizioni in cui la sua energia cinetica è zero e (b) le forze in quelle posizioni.
Strategia
(a) Possiamo trovare le posizioni in cui
![]()
quindi l’energia potenziale è uguale all’energia totale del sistema dato. (b) Utilizzando (Figura), possiamo trovare la forza valutata nelle posizioni trovate dalla parte precedente, poiché l’energia meccanica è conservata.
Soluzione
- energia totale di un sistema di 2 J è uguale alla quartica energia elastica come dato del problema,

la Risoluzione per
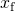
risultati in
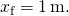
- Da (Figura),
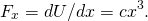
Quindi, valutare la forza
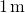
, abbiamo
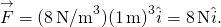
In entrambe le posizioni, la grandezza delle forze è di 8 N e le indicazioni verso l’origine, poiché questo è il potenziale energia per una forza di ripristino.
Significato
Trovare la forza dall’energia potenziale è matematicamente più facile che trovare l’energia potenziale dalla forza, perché differenziare una funzione è generalmente più facile che integrarne una.
Controlla la tua comprensione
Trova le forze sulla particella in (Figura) quando la sua energia cinetica è 1.0 J a
![]()
Soluzione Spettacolo
![]()
diretto verso l’origine
Sommario
- Una forza conservatrice è quello per il quale il lavoro fatto è indipendente dal percorso. Equivalentemente, una forza è conservativa se il lavoro svolto su qualsiasi percorso chiuso è zero.
- Una forza non conservativa è quella per la quale il lavoro svolto dipende dal percorso.
- Per una forza conservativa, il lavoro infinitesimale è un differenziale esatto. Ciò implica condizioni sulle derivate dei componenti della forza.
- La componente di una forza conservativa, in una particolare direzione, è uguale al negativo della derivata dell’energia potenziale per quella forza, rispetto a uno spostamento in quella direzione.
Domande concettuali
Qual è il significato fisico di una forza non conservatrice?
Mostra Soluzione
Una forza che toglie energia al sistema che non può essere recuperata se dovessimo invertire l’azione.
Un razzo bottiglia viene sparato verso l’alto in aria con una velocità
![]()
. Se la resistenza dell’aria viene ignorata, la bottiglia salirebbe ad un’altezza di circa
![]()
. Tuttavia, il razzo va fino a solo
![]()
prima di tornare a terra. Che cos’è successo? Spiega, dando solo una risposta qualitativa.
Una forza esterna agisce su una particella durante un viaggio da un punto all’altro e di nuovo a quello stesso punto. Questa particella è effettuata solo da forze conservative. L’energia cinetica e l’energia potenziale di questa particella cambiano come risultato di questo viaggio?
Mostra Soluzione
La variazione di energia cinetica è il lavoro netto. Poiché le forze conservative sono indipendenti dal percorso, quando si torna allo stesso punto le energie cinetiche e potenziali sono esattamente le stesse dell’inizio. Durante il viaggio l’energia totale viene conservata, ma cambiano sia l’energia potenziale che quella cinetica.
Problemi
Una forza
![]()
agisce su una particella mentre si muove lungo l’asse x positivo. (a) Quanto lavoro fa la forza sulla particella mentre si muove da
![]()
a
![]()
(b) Scegliere un punto di riferimento conveniente dell’energia potenziale da azzerare
![]()
trova l’energia potenziale per questa forza.
Una forza
![]()
agisce su una particella. (a) Quanto lavoro fa la forza sulla particella mentre si muove da
![]()
a
![]()
(b) Scegliere un punto di riferimento conveniente dell’energia potenziale da azzerare
![]()
trova l’energia potenziale per questa forza.
Soluzione Spettacolo
![]()
Trovare la forza corrispondente all’energia potenziale
![]()
L’energia potenziale funzione per uno dei due atomi in una molecola biatomica è spesso approssimata da
![]()
dove x è la distanza tra gli atomi. (a) A quale distanza di separazione l’energia potenziale ha un minimo locale (non a
![]()
(b) Qual è la forza su un atomo a questa separazione? (c) Come varia la forza con la distanza di separazione?
Mostra soluzione
a.
![]()
; b.
![]()
; c.
![]()
Una particella di massa
![]()
si muove sotto l’influenza della forza
![]()
Se la sua velocità a
![]()
è
![]()
qual è la sua velocità di
![]()
Una particella di massa
![]()
si muove sotto l’influenza della forza
![]()
Se la sua velocità a
![]()
è
![]()
qual è la sua velocità di
![]()
Soluzione Spettacolo
![]()
Una gabbia a rulli è spinto senza attrito perdita di energia attraverso il piano di un automobile di trasporto (vedere la figura seguente). L’auto si muove a destra con una velocità costante
![]()
Se la cassa inizia a riposo rispetto al vagone merci, quindi dal teorema dell’energia del lavoro,
![]()
dove d, la distanza della cassa si muove, e v, la velocità della cassa, sono entrambi misurati rispetto al vagone merci. (a) Ad un osservatore a riposo accanto ai binari, a quale distanza
![]()
la cassa viene spinta quando sposta la distanza d nell’auto? (b) Quali sono le velocità iniziali e finali della cassa
![]()
e
![]()
come misurato dall’osservatore accanto alle tracce? c) Dimostrare che
![]()
e, di conseguenza, che il lavoro è uguale al cambiamento di energia cinetica in entrambi i sistemi di riferimento.

Glossario
forza conservativa forza che funziona indipendentemente dal percorso differenziale esatto è il differenziale totale di una funzione e richiede l’uso di derivate parziali se la funzione coinvolge più di una dimensione forza non conservativa forza che funziona che dipende dal percorso
Leave a Reply