大学物理学第1巻1
8
学習目標
このセクションの終わりまでに、あなたは次のことができるようになります:
- いくつかの異なる方法で保守力を特徴付ける
- 保守力によって満たされなければならない数学的条件を指定し、その成分
- 系の粒子間の保守力を系のポテンシャルエネルギーに関連付ける
- 様々な場合における保守力の成分を計算する
ポテンシャルエネルギーとエネルギーの保存において,運動エネルギーとポテンシャルエネルギーの間の任意の遷移は系の全エネルギーを保存した。 これは経路に依存せず、問題の任意の2つの点で開始および停止することができ、これらの点でのシステムの総エネルギー—運動性とポテンシャル—は互いに等しいことを意味します。 これは保守的な力の特徴です。 前節では,重力やばね力などの保守的な力を扱った。 (図)でサッカーの動きを比較すると、サッカーの重力ポテンシャルエネルギーが増加しても、ボールが地面に対して上昇し、サッカー選手がボールをキャッチしたときに最初の重力ポテンシャルエネルギーに戻るため、システムの総エネルギーは変化しません。 非保守的な力は、摩擦や空気抵抗などの散逸力です。 これらの力は、システムが進行するにつれてシステムからエネルギーを奪い、あなたが取り戻すことができないエネルギーを奪います。 これらの力はパスに依存するため、オブジェクトの開始位置と停止位置が重要です。
保守的な力
保守的な力によって行われる作業は、パスとは独立しています;言い換えると、保守的な力によって行われる作業は、二つの点を結ぶ任意の:
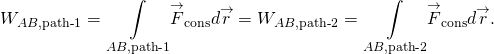
非保守的な力によって行われる作業は、取られた経路に依存する。
同様に、任意の閉じたパスの周りで行う作業がゼロであれば、力は保守的です:
![]()
(figure)と(Figure)は、任意の閉じたパスが2つのパスの合計であるため、同等です: BからAへのパスに沿って行われた作業は、AからBへの同じパスに沿って行われた作業の負であり、AとBは閉じたパス上の任意の二つの点です:
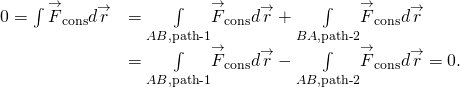
定義にはAからBへのすべてのパス、またはすべての閉じたパスが含まれているため、力が保守的であるかどうかを証明する方法を尋ねるかもし 一つの答えは、行われた作業は、無限小の作業の場合、パスとは独立しているということです
![]()
は正確な微分であり、無限小の正味の仕事が運動エネルギーの正確な微分に等しい方法です,
![]()
仕事-エネルギー定理で仕事-エネルギー定理を導出したとき。 力によって行われた無限小の作業が正確な微分であり、力が保守的であるかどうかをテストするために使用できる数学的条件があります。 これらの条件は分化を伴うだけであり、したがって適用が比較的容易である。 二次元では、のための条件
![]()
正確な微分であるためには、次のようになります
![]()
あなたは(図)の力によって行われた作業は、パスに依存していることを思い出すことができます。 その力のために,
![]()
したがって、,
![]()
それは非保守的な力であることを示しています。 あなたはそれを保守的な力にするために何を変えることができるかを見ることができますか?

例
保守的かどうか?
以下の二次元力のうち、どれが保守的で、どれが保守的でないのか? Aとbが適切な単位を持つ定数であると仮定します:
()
![]()
(b)
![]()
(c)
![]()
戦略
は、(図)に記載されている条件、すなわち、示されている各力の成分の導関数を使用して適用します。 Xに関する力のy成分の導関数がyに関する力のx成分の導関数と等しい場合、力は保守的な力であり、ポテンシャルエネルギーまたは仕事の計算に取られた経路は常に同じ結果をもたらすことを意味する。
-
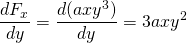
と
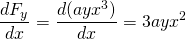
, だから、この力は非保守的です。
-
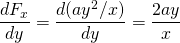
と
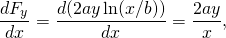
だから、この力は保守的です。
-
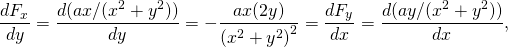
再び保守的。
有意性
(図)の条件は、単一の変数の関数としての導関数であり、三次元では、より多くの導関数を含む同様の条件が存在する。
あなたの理解を確認してください
二次元の保守的な力は、x軸とy軸でゼロであり、次の条件を満たします
![]()
. その時点での力の大きさは何ですか
![]()
ソリューションを表示
2.83N
このセクションを離れる前に、エネルギーがシステムに失われ、後で有用な作業に変換することができないため、非保守的な力には潜在的なエネルギーが関連していないことに注意してください。 だから、すべての潜在的なエネルギーに関連する保守的な力が常にあります。 私たちは、潜在的なエネルギーが保守的な力によって行われた仕事に関連して定義されていることを見てきました。 力と変位から始めて、あなたは仕事と潜在的なエネルギーの変化を得るために統合しました。 あなたも同様にポテンシャルエネルギーから始めて、変位に関してその導関数を取って力を得ることができました。 ポテンシャルエネルギーの無限小の増分は、力と無限小の変位の内積です,
![]()
ここでは、任意の方向への変位を次のように表現することを選択しました
![]()
任意の特定の座標方向に限定されないようにする。 また,無限小変位の大きさとその方向の力の成分によって内積を表現した。 これらの量は両方ともスカラーなので、dlで除算して得ることができます
![]()
この方程式は、力とそれに関連するポテンシャルエネルギーとの関係を与える。 言い換えれば、特定の方向における保守的な力の成分は、その方向の変位に関して、対応するポテンシャルエネルギーの導関数の負の値に等しい。 一次元運動の場合、x軸に沿って言うと、(図)はベクトル全体の力を与えます,
![]()
二次元で,
![]()
この方程式から、力の成分の導関数の観点から、仕事が正確な微分であるための条件である理由(図)を見ることができます。 一般に、偏微分記法が使用される。 関数に多くの変数が含まれている場合、偏導関数が指定する変数の導関数のみが取得されます。 他の変数は一定に保持されます。 3次元では、z成分に別の項を追加すると、力はポテンシャルエネルギーの勾配の負の値になります。 しかし、私たちはまだ三次元の例を見ていません。
例
四次ポテンシャルエネルギーによる力
x軸に沿って一次元運動を受けている粒子のポテンシャルエネルギーは次のとおりです
![]()
どこで
![]()
その総エネルギーで
![]()
そして、それは非保守的な力の対象ではありません。 (A)その運動エネルギーがゼロである位置と(b)それらの位置での力を求めます。
戦略
(a)位置を見つけることができます
![]()
そのため、ポテンシャルエネルギーは与えられたシステムの総エネルギーに等しくなります。 (b)(図)を使用すると、機械的エネルギーが保存されているため、前の部分から見つかった位置で評価された力を見つけることができます。
解
- 2Jの系の総エネルギーは、問題で与えられた四次弾性エネルギーに等しくなります,

のための解決
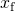
結果は
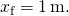
- から(図),
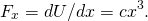
従って、力をで評価すること
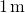
, 私達は得ます
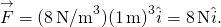
両方の位置で、力の大きさは8Nであり、方向は原点に向かっています。 復元力のためのエネルギー。
有意性
ポテンシャルエネルギーから力を求めることは、力からポテンシャルエネルギーを求めるよりも数学的に簡単です。
あなたの理解を確認してください
運動エネルギーが1のときの粒子への力を(図)で求めます。0Jで
![]()
ソリューションを表示
![]()
原点に向けて
概要
- 保守的な力は、行われた作業がパスとは独立している力です。 同様に、任意の閉じた経路上で行われた作業がゼロである場合、力は保守的です。
- 非保守的な力は、行われる作業が経路に依存する力です。
- 保守的な力の場合、無限小の仕事は正確な微分です。 これは力の成分の導関数に関する条件を意味する。
- 保守的な力の成分は、特定の方向では、その方向への変位に関して、その力のポテンシャルエネルギーの導関数の負の値に等しくなります。
概念的な質問
非保守的な力の物理的な意味は何ですか?
解決策を示す
システムからエネルギーを奪う力で、行動を逆転させた場合には回復できません。
ボトルロケットは、速度で空気中でまっすぐに撃たれます
![]()
. 空気抵抗が無視されれば、びんはおよその高さに上がります
![]()
. しかし、ロケットは唯一に上がります
![]()
地面に戻る前に。 どうしました? 定性的な応答のみを与えて説明してください。
外力は、ある点から別の点への移動中に粒子に作用し、その同じ点に戻る。 この粒子は保守的な力によってのみ影響されます。 この粒子の運動エネルギーとポテンシャルエネルギーは、この旅行の結果として変化しますか?
解を表示
運動エネルギーの変化は正味の仕事です。 保守的な力は経路に依存しないので、あなたが同じ点に戻っているとき、運動エネルギーと潜在的なエネルギーは始まりとまったく同じです。 旅の間、総エネルギーは保存されますが、ポテンシャルエネルギーと運動エネルギーの両方が変化します。
問題点
ア-フォース
![]()
パーティクルが正のx軸に沿って移動するときにパーティクルに作用します。 (a)力がパーティクルから移動するときにどのくらいの仕事をしますか
![]()
に
![]()
(b)でゼロになるようにポテンシャルエネルギーの便利な基準点を選ぶ
![]()
この力の潜在的なエネルギーを見つけます。
ア-フォース
![]()
粒子に作用する。 (a)力がパーティクルから移動するときにどのくらいの仕事をしますか
![]()
に
![]()
(b)でゼロになるようにポテンシャルエネルギーの便利な基準点を選ぶ
![]()
この力の潜在的なエネルギーを見つけます。
ソリューションを表示
![]()
ポテンシャルエネルギーに対応する力を求める
![]()
二原子分子内の二つの原子のいずれかのためのポテンシャルエネルギー関数は、多くの場合、次のように近似されます
![]()
ここで、xは原子間の距離である。 (a)分離のどの距離で、ポテンシャルエネルギーは極小値を持っていますか(ではありません
![]()
(b)この分離時の原子への力は何ですか? (c)力は分離距離によってどのように変化しますか?
ソリューションを表示
a.
![]()
; b.
![]()
; c.
![]()
質量の粒子
![]()
力の影響を受けて移動する
![]()
での速度ならば、
![]()
は
![]()
その速度は何ですか
![]()
質量の粒子
![]()
力の影響を受けて移動する
![]()
での速度ならば、
![]()
![]()
その速度は何ですか
![]()
ソリューションを表示
![]()
ローラーの木枠は貨物車の床を渡るエネルギーの摩擦損失なしで押されている(次の図を見なさい)。 車は一定の速度で右に移動しています
![]()
クレートが貨物車に対して安静時に始まる場合、作業エネルギー定理から,
![]()
ここで、d、クレートが移動する距離、およびv、クレートの速度は、両方とも貨物車に対する相対的に測定されます。 (a)トラックの横に休息している観察者に、どのような距離
![]()
それは車の中で距離dを移動するときに木枠が押されていますか? (b)クレートの初期速度と最終速度は何ですか
![]()
と
![]()
トラックの横にある観察者によって測定されたように? (c)それを示す
![]()
そして、その結果、その仕事は両方の参照系における運動エネルギーの変化に等しい。
用語集
パスに依存しない作業を行う保守的な力力正確な微分は、関数の全微分であり、関数が複数の次元を含む場合は偏導関数の使用を必要とします非保守的な力パスに依存する作業を行う力
Leave a Reply