Universitetsfysikkvolum 1
8 Potensiell Energi Og Bevaring Av Energi
Læringsmål
ved slutten av denne delen vil du kunne:
- Karakteriser en konservativ kraft på flere forskjellige måter
- Spesifiser matematiske forhold som må oppfylles av en konservativ kraft og dens komponenter
- Relatere den konservative kraften mellom partikler i et system til den potensielle energien i systemet
- Beregn komponentene til en konservativ kraft i ulike tilfeller
I Potensiell Energi og Bevaring av Energi, enhver overgang mellom kinetisk og potensiell energi bevart den totale energien i systemet. Dette var sti uavhengig, noe som betyr at vi kan starte og stoppe på noen to punkter i problemet, og systemets totale energi-kinetisk pluss potensial – på disse punktene er lik hverandre. Dette er karakteristisk for en konservativ kraft. Vi jobbet med konservative krefter i den foregående delen, som gravitasjonskraften og vårkraften. Når man sammenligner bevegelsen av fotball i (Figur), den totale energien i systemet aldri endres, selv om gravitasjons potensiell energi av fotball øker, som ballen stiger i forhold til bakken og faller tilbake til den opprinnelige gravitasjons potensiell energi når fotballspilleren fanger ballen. Ikke-konservative krefter er dissipative krefter som friksjon eller luftmotstand. Disse kreftene tar energi bort fra systemet når systemet utvikler seg, energi som du ikke kan få tilbake. Disse kreftene er baneavhengige; derfor er det viktig hvor objektet starter og stopper.
Konservativ Kraft
arbeidet utført Av en konservativ kraft er uavhengig av banen; med andre ord, arbeidet utført Av en konservativ kraft er det samme for enhver sti som forbinder to punkter:
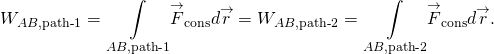
arbeidet som utføres av en ikke-konservativ kraft, avhenger av banen som er tatt.
Tilsvarende er en kraft konservativ hvis arbeidet den gjør rundt en lukket bane er null:
![]()
(Figur) Og (Figur) er ekvivalente fordi en lukket bane er summen av to baner: den første går Fra A Til B, og den andre går Fra B Til A. arbeidet som går langs en sti Fra B Til A er det negative av arbeidet som går langs samme sti Fra A Til B, Hvor A Og B er to punkter på den lukkede banen:
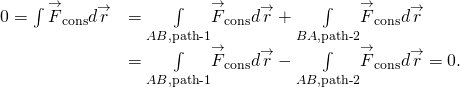
Du kan spørre hvordan vi går om å bevise om en kraft er konservativ, siden definisjonene involverer alle veier Fra A Til B, eller alle lukkede baner, men for å gjøre integralet for arbeidet må du velge en bestemt sti. Et svar er at arbeidet er uavhengig av banen hvis det uendelige arbeidet
![]()
er en eksakt differensial, måten infinitesimal netto arbeid var lik den eksakte differensial av kinetisk energi,
![]()
når vi avledet arbeid-energi teoremet I Arbeid-Energi Teoremet. Det er matematiske forhold som du kan bruke til å teste om det uendelige arbeidet med en kraft er en eksakt differensial, og kraften er konservativ. Disse forholdene involverer bare differensiering og er dermed relativt enkle å anvende. I to dimensjoner er betingelsen for
![]()
for å være en nøyaktig differensial er
![]()
Du husker kanskje at arbeidet som ble gjort av kraften i (Figur) var avhengig av banen. For denne styrken,
![]()
Derfor,
![]()
som indikerer at det er en ikke-konservativ kraft. Kan du se hva du kan endre for å gjøre det til en konservativ kraft?

Eksempel
Konservativ eller Ikke?
Hvilke av de følgende todimensjonale kreftene er konservative og hvilke er ikke? Anta a og b er konstanter med passende enheter:
(a)
![]()
(b)
![]()
(c)
![]()
Strategi
Bruk betingelsen angitt i (Figur), nemlig ved bruk av derivatene av komponentene til hver kraft som er angitt. Hvis derivatet av y-komponenten av kraften i forhold til x er lik derivatet av x-komponenten av kraften i forhold til y, er kraften en konservativ kraft, noe som betyr at banen tatt for potensiell energi eller arbeidsberegninger alltid gir de samme resultatene.
Løsning
-
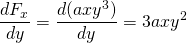
og
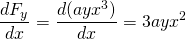
, så denne kraften er ikke-konservativ.
-
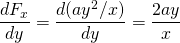
og
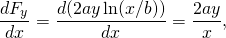
så denne kraften er konservativ.
-
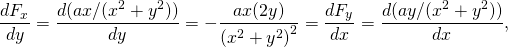
igjen konservativ.
Signifikans
betingelsene I (Figur) er derivater som funksjoner av en enkelt variabel; i tre dimensjoner eksisterer lignende forhold som involverer flere derivater.
Sjekk Din Forståelse
en todimensjonal, konservativ kraft er null på x-og y-aksene, og tilfredsstiller betingelsen
![]()
. Hva er størrelsen på kraften på punktet
![]()
Vis Løsning
2,83 N
Før vi forlater denne delen, bemerker vi at ikke-konservative krefter ikke har potensiell energi forbundet med dem fordi energien går tapt for systemet og ikke kan omdannes til nyttig arbeid senere. Så det er alltid en konservativ kraft forbundet med enhver potensiell energi. Vi har sett at potensiell energi er definert i forhold til arbeidet utført av konservative krefter. Det forholdet, (Figur), innebar en integrert for arbeidet; starter med kraft og forskyvning, integrert du for å få arbeidet og endringen i potensiell energi. Integrasjon er imidlertid den inverse driften av differensiering; du kunne like godt ha startet med potensiell energi og tatt dens derivat, med hensyn til forskyvning, for å få kraften. Den uendelige økningen av potensiell energi er prikkproduktet av kraften og den uendelige forskyvningen,
![]()
Her valgte vi å representere forskyvningen i en vilkårlig retning av
![]()
for ikke å være begrenset til en bestemt koordinatretning. Vi uttrykte også prikkproduktet når det gjelder størrelsen på den uendelige forskyvningen og komponenten av kraften i dens retning. Begge disse mengdene er skalarer, slik at du kan dele med dl for å få
![]()
denne ligningen gir forholdet mellom kraft og potensiell energi forbundet med den. I ord er komponenten av en konservativ kraft, i en bestemt retning, lik den negative av derivatet av den tilsvarende potensielle energien, med hensyn til en forskyvning i den retningen. For endimensjonal bevegelse, si langs x-aksen, (Figur) gi hele vektorkraften,
![]()
I to dimensjoner,
![]()
fra denne ligningen kan du se hvorfor (Figur) er betingelsen for at arbeidet skal være en nøyaktig differensial, når det gjelder derivatene av kraftens komponenter. Generelt brukes en delvis derivat notasjon. Hvis en funksjon har mange variabler i den, blir derivatet bare tatt av variabelen den delvise derivatet spesifiserer. De andre variablene holdes konstant. I tre dimensjoner legger du til et annet begrep for z-komponenten, og resultatet er at kraften er negativ av gradienten av potensiell energi. Vi vil imidlertid ikke se på tredimensjonale eksempler ennå.
Eksempel
Kraft på Grunn Av En Kvart Potensiell Energi
den potensielle energien for en partikkel som gjennomgår endimensjonal bevegelse langs x-aksen er
![]()
hvor
![]()
dens totale energi på
![]()
og det er ikke underlagt noen ikke-konservative krefter. Finn (a) posisjonene der den kinetiske energien er null og (b) kreftene i disse posisjonene.
Strategi
(a) Vi kan finne stillingene der
![]()
så den potensielle energien er lik den totale energien til det gitte systemet. (B) Ved Hjelp Av (Figur) kan vi finne kraften evaluert ved posisjonene funnet fra forrige del, siden den mekaniske energien er bevart.
Løsning
- den totale energien til systemet med 2 J er lik den kvartære elastiske energien som gitt i problemet,

Løsning for
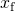
resultater i
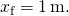
- Fra (Figur),
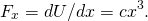
dermed vurderer kraften på
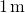
, vi får
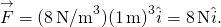
i begge posisjoner er størrelsen på kreftene 8 N Og retningene er mot opprinnelsen, siden dette er potensialet energi for a gjenopprette kraften.
Betydning
Å Finne kraften Fra den potensielle energien er matematisk lettere enn å finne den potensielle energien fra kraften, fordi differensiering av en funksjon er generelt lettere enn å integrere en.
Sjekk Din Forståelse
Finn kreftene på partikkelen i (Figur) når den kinetiske energien er 1.0 j på
![]()
Vis Løsning
![]()
rettet mot opprinnelsen
Sammendrag
- en konservativ kraft er en som arbeidet er uavhengig av banen. Tilsvarende er en kraft konservativ hvis arbeidet over en lukket bane er null.
- en ikke-konservativ kraft er en som arbeidet er avhengig av banen.
- for en konservativ kraft er det uendelige arbeidet en eksakt differensial. Dette innebærer forhold på derivatene av kraftens komponenter.
- komponenten av en konservativ kraft, i en bestemt retning, er lik den negative av derivatet av den potensielle energien for den kraften, med hensyn til en forskyvning i den retningen.
Konseptuelle Spørsmål
Hva er den fysiske betydningen av en ikke-konservativ kraft?
Vis Solution
en kraft som tar energi bort fra systemet som ikke kan gjenopprettes hvis vi skulle reversere handlingen.
en flaske rakett er skutt rett opp i luften med en hastighet
![]()
. Hvis luftmotstanden ignoreres, vil flasken gå opp til en høyde på ca.
![]()
. Men raketten går opp til bare
![]()
før du går tilbake til bakken. Hva skjedde? Forklar, gir bare et kvalitativt svar.
en ekstern kraft virker på en partikkel under en tur fra ett punkt til et annet og tilbake til det samme punktet. Denne partikkelen utføres bare av konservative krefter. Endrer partikkelens kinetiske energi og potensielle energi som følge av denne turen?
Vis Løsning
endringen i kinetisk energi er netto arbeid. Siden konservative krefter er sti uavhengige, når du er tilbake til samme punkt, er kinetiske og potensielle energier nøyaktig det samme som begynnelsen. Under turen blir den totale energien bevart, men både potensiell og kinetisk energi endres.
Problemer
en kraft
![]()
virker på en partikkel når den beveger seg langs den positive x-aksen. (A) Hvor mye arbeid gjør kraften på partikkelen når den beveger seg fra
![]()
til
![]()
(B) Velge et passende referansepunkt for den potensielle energien til å være null ved
![]()
finn den potensielle energien for denne kraften.
en kraft
![]()
handler på en partikkel. (A) Hvor mye arbeid gjør kraften på partikkelen når den beveger seg fra
![]()
til
![]()
(B) Velge et passende referansepunkt for den potensielle energien til å være null ved
![]()
finn den potensielle energien for denne kraften.
Vis Løsning
![]()
Finn kraften som svarer til potensiell energi
![]()
den potensielle energifunksjonen for ett av de to atomene i et diatomisk molekyl er ofte tilnærmet av
![]()
hvor x er avstanden mellom atomene. (a) på hvilken avstand av separasjon har potensiell energi et lokalt minimum (ikke på
![]()
(b) Hva er kraften på et atom ved denne separasjonen? (c) hvordan varierer kraften med separasjonsavstanden?
Vis Løsning
a.
![]()
; b.
![]()
; c.
![]()
en partikkel av masse
![]()
beveger seg under påvirkning av kraften
![]()
hvis hastigheten på
![]()
er
![]()
hva er hastigheten på
![]()
en partikkel av masse
![]()
beveger seg under påvirkning av kraften
![]()
hvis hastigheten på
![]()
er
![]()
hva er hastigheten på
![]()
Vis Løsning
![]()
en kasse på ruller skyves uten friksjonstap av energi over gulvet i en godsvogn(se følgende figur). Bilen beveger seg til høyre med konstant fart
![]()
hvis kassen starter i ro i forhold til godsvognen, så fra arbeidsenergiteoremet,
![]()
hvor d, avstanden kassen beveger seg, og v, kassens hastighet, måles begge i forhold til godsvognen. (a) til en observatør i ro ved siden av sporene, hvilken avstand
![]()
er kassen presset når den beveger avstanden d i bilen? (b) hva er kassens innledende og endelige hastigheter
![]()
og
![]()
som målt av observatøren ved siden av sporene? (C) Viser at
![]()
og følgelig er dette arbeidet lik endringen i kinetisk energi i begge referansesystemene.

Ordliste
konservativ kraftkraft som virker uavhengig av banens eksakte differensial er den totale differensialen til en funksjon og krever bruk av partielle derivater hvis funksjonen innebærer mer enn en dimensjon ikke-konservativ kraftkraft som virker som avhenger av banen
Leave a Reply