Universiteitsfysica deel 1 1
8 potentiële energie en energiebesparing
leerdoelstellingen
aan het einde van deze sectie kunt u:
- Karakteriseren van een conservatieve kracht in verschillende manieren
- Geef de wiskundige voorwaarden waaraan moet worden voldaan door een conservatieve kracht en de componenten
- hebben Betrekking op de conservatieve kracht tussen de deeltjes van een systeem om de potentiële energie van het systeem
- Bereken de componenten van een conservatieve kracht in verschillende gevallen
In Potentiële Energie en Behoud van Energie, een overgang tussen kinetische en potentiële energie behouden de totale energie van het systeem. Dit was pad onafhankelijk, wat betekent dat we kunnen beginnen en stoppen op twee punten in het probleem, en de totale energie van het systeem—kinetisch plus potentieel—op deze punten zijn gelijk aan elkaar. Dit is kenmerkend voor een conservatieve kracht. In het vorige hoofdstuk hebben we het gehad over conservatieve krachten, zoals de gravitatiekracht en de veerkracht. Bij het vergelijken van de beweging van de voetbal in (Figuur), de totale energie van het systeem nooit verandert, hoewel de gravitationele potentiële energie van de voetbal toeneemt, als de bal stijgt ten opzichte van de grond en valt terug naar de initiële gravitationele potentiële energie wanneer de voetballer vangt de bal. Niet-conservatieve krachten zijn dissipatieve krachten zoals wrijving of luchtweerstand. Deze krachten nemen energie weg van het systeem als het systeem vordert, energie die je niet terug kunt krijgen. Deze krachten zijn padafhankelijk; daarom is het belangrijk waar het object begint en stopt.
conservatieve kracht
het werk van een conservatieve kracht is onafhankelijk van het pad; met andere woorden, het werk van een conservatieve kracht is hetzelfde voor elk pad dat twee punten verbindt:
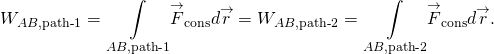
het werk van een niet-conservatieve kracht hangt af van de ingeslagen weg.
op equivalente wijze is een kracht conservatief als het werk dat het doet rond een gesloten pad nul is:
![]()
(figuur) en (figuur) zijn gelijkwaardig omdat elk gesloten pad de som is van twee paden: de eerste gaat van A naar B, en de tweede gaat van B naar A. Het werk gaat langs een pad van B naar A is het negatief van het werk gaat langs hetzelfde pad van A naar B, waar A en B elk twee punten op het gesloten pad zijn:
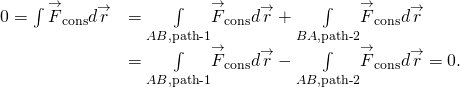
je kunt je afvragen hoe we gaan bewijzen of een kracht wel of niet conservatief is, omdat de definities alle paden van A naar B omvatten, of alle gesloten paden, maar om de integraal voor het werk te doen, moet je een bepaald pad kiezen. Een antwoord is dat het werk dat wordt gedaan onafhankelijk is van het pad als het infinitesimale werk
![]()
is een exact differentieel, de manier waarop het infinitesimale netwerk gelijk was aan het exacte differentieel van de kinetische energie,
![]()
toen we de werk-energiestelling in de werk-Energiestelling afgeleid. Er zijn wiskundige voorwaarden die je kunt gebruiken om te testen of het infinitesimale werk gedaan door een kracht is een exacte differentieel, en de kracht is conservatief. Deze voorwaarden houden alleen differentiatie in en zijn dus relatief eenvoudig toe te passen. In twee dimensies, de voorwaarde voor
![]()
om een exact verschil te zijn is
![]()
u herinnert zich misschien dat het werk van de kracht in (Figuur) afhing van het pad. Voor die kracht,
![]()
daarom,
![]()
wat aangeeft dat het een niet-conservatieve kracht is. Zie je wat je kunt veranderen om er een conservatieve kracht van te maken?

voorbeeld
conservatief of niet?
welke van de volgende tweedimensionale krachten zijn conservatief en welke niet? Stel dat A en b constanten zijn met de juiste eenheden:
(a)
![]()
(b)
![]()
(c)
![]()
strategie
Pas de in (Figuur) vermelde voorwaarde toe, namelijk, gebruikmakend van de afgeleiden van de componenten van elke aangegeven kracht. Als de afgeleide van de y-component van de kracht ten opzichte van x gelijk is aan de afgeleide van de x-component van de kracht ten opzichte van y, is de kracht een conservatieve kracht, wat betekent dat het pad dat wordt genomen voor potentiële energie-of werkberekeningen altijd dezelfde resultaten oplevert.
oplossing
-
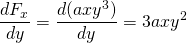
en
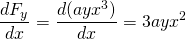
, dus deze kracht is niet-conservatief.
-
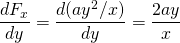
en
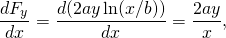
dus deze kracht is conservatief.
-
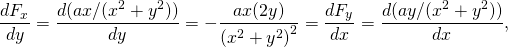
weer conservatief.
significantie
de voorwaarden in (figuur) zijn derivaten als functies van een enkele variabele; in drie dimensies bestaan vergelijkbare voorwaarden die meer derivaten omvatten.
Controleer uw begrip
een tweedimensionale, conservatieve kracht is nul op de x-en y-as, en voldoet aan de voorwaarde
![]()
. Wat is de grootte van de kracht op het punt
![]()
oplossing
2,83 N tonen
voordat we deze sectie verlaten, merken we op dat niet-conservatieve krachten geen potentiële energie hebben die ermee geassocieerd is omdat de energie verloren gaat aan het systeem en niet later in nuttig werk kan worden omgezet. Er is dus altijd een conservatieve kracht verbonden met elke potentiële energie. We hebben gezien dat potentiële energie wordt gedefinieerd in relatie tot het werk van conservatieve krachten. Die relatie, (figuur), omvatte een integraal voor het werk; te beginnen met de kracht en verplaatsing, integreerde je om het werk en de verandering in potentiële energie te krijgen. Integratie is echter de omgekeerde werking van differentiatie; je had net zo goed kunnen beginnen met de potentiële energie en zijn afgeleide kunnen nemen, met betrekking tot verplaatsing, om de kracht te krijgen. De infinitesimale toename van potentiële energie is het puntproduct van de kracht en de infinitesimale verplaatsing,
![]()
hier hebben we ervoor gekozen om de verplaatsing in een willekeurige richting weer te geven door
![]()
om niet te worden beperkt tot een bepaalde coördinatenrichting. We hebben het puntproduct ook uitgedrukt in termen van de grootte van de infinitesimale verplaatsing en de component van de kracht in zijn richting. Beide hoeveelheden zijn scalaren, dus je kunt delen door dl te krijgen
![]()
deze vergelijking geeft de relatie tussen kracht en de potentiële energie die ermee verbonden is. In woorden, de component van een conservatieve kracht, in een bepaalde richting, is gelijk aan het negatief van de afgeleide van de overeenkomstige potentiële energie, met betrekking tot een verplaatsing in die richting. Voor eendimensionale beweging, zeg langs de x-as, (figuur) geef de volledige vectorkracht,
![]()
In twee dimensies,
![]()
uit deze vergelijking kun je zien waarom (figuur) de voorwaarde is voor het werk om een exact differentieel te zijn, in termen van de afgeleiden van de componenten van de kracht. In het algemeen wordt een partiële afgeleide notatie gebruikt. Als een functie veel variabelen bevat, wordt de afgeleide alleen genomen van de variabele die de partiële afgeleide specificeert. De andere variabelen worden constant gehouden. In drie dimensies voeg je een andere term toe voor de Z-component, en het resultaat is dat de kracht het negatieve is van de gradiënt van de potentiële energie. We zullen echter nog niet naar driedimensionale voorbeelden kijken.
Voorbeeld
Kracht vanwege een Quartic Potentiële Energie
De potentiële energie van een deeltje ondergaat één-dimensionale beweging langs de x-as is
![]()
waar
![]()
De totale energie op
![]()
en het is niet onderworpen aan een niet-conservatieve krachten. Zoek (a) de posities waar de kinetische energie nul is en (b) de krachten op die posities.
strategie
(a) We kunnen de posities vinden waar
![]()
dus de potentiële energie is gelijk aan de totale energie van het gegeven systeem. (B) met behulp van (figuur), kunnen we de kracht geëvalueerd op de posities gevonden uit het vorige deel, omdat de mechanische energie wordt behouden.
Oplossing
- De totale energie van het systeem van 2 J is gelijk aan de quartic elastische energie zoals gegeven in het probleem,

voor het Oplossen van
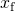
resultaten in
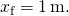
- Uit (Figuur),
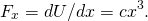
Dus, het evalueren van de werking getreden op
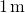
, we krijgen
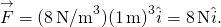
Op beide posities, de grootte van de krachten is 8 N en de aanwijzingen zijn in de richting van de oorsprong, omdat dit de potentieel energie voor een herstellende kracht.
Betekenis
het vinden van de kracht uit de potentiële energie is wiskundig eenvoudiger dan het vinden van de potentiële energie uit de kracht, omdat het differentiëren van een functie over het algemeen gemakkelijker is dan er een te integreren.
Controleer uw begrip
Zoek de krachten op het deeltje in (figuur) wanneer de kinetische energie 1 is.0 J at
![]()
oplossing tonen
![]()
gericht op de oorsprong
samenvatting
- een conservatieve kracht is er een waarvoor het verrichte werk onafhankelijk is van path. Op gelijkwaardige wijze is een kracht conservatief als het werk over een gesloten pad nul is.
- een niet-conservatieve kracht is er een waarvan het werk afhankelijk is van het pad.
- voor een conservatieve kracht is het infinitesimale werk een exact differentieel. Dit impliceert voorwaarden voor de afgeleiden van de componenten van de kracht.
- de component van een conservatieve kracht in een bepaalde richting is gelijk aan het negatief van de afgeleide van de potentiële energie voor die kracht ten opzichte van een verplaatsing in die richting.
conceptuele vragen
Wat is de fysieke betekenis van een niet-conservatieve kracht?
Toon oplossing
een kracht die energie uit het systeem haalt die niet kan worden teruggewonnen als we de actie omkeren.
een fles raket wordt geschoten recht omhoog in de lucht met een snelheid
![]()
. Als de luchtweerstand wordt genegeerd, zou de fles gaan tot een hoogte van ongeveer
![]()
. Echter, de raket gaat tot slechts
![]()
voordat hij terug naar de grond ging. Wat is er gebeurd? Leg uit, geef alleen een kwalitatieve reactie.
een externe kracht werkt op een deeltje tijdens een reis van het ene punt naar het andere en terug naar hetzelfde punt. Dit deeltje wordt alleen beïnvloed door conservatieve krachten. Verandert de kinetische energie en potentiële energie van dit deeltje als gevolg van deze reis?
oplossing
de verandering in kinetische energie is het net. Omdat conservatieve krachten padonafhankelijk zijn, zijn wanneer je terug bent op hetzelfde punt de kinetische en potentiële energieën precies hetzelfde als het begin. Tijdens de reis wordt de totale energie behouden, maar zowel de potentiële als de kinetische energie veranderen.
problemen
een kracht
![]()
werkt op een deeltje als het langs de positieve x-as beweegt. (a) hoeveel werk doet de kracht op het deeltje als het beweegt van
![]()
aan
![]()
(b) het kiezen van een geschikt referentiepunt van de potentiële energie om nul te zijn op
![]()
zoek de potentiële energie voor deze kracht.
een kracht
![]()
werkt op een deeltje. (a) hoeveel werk doet de kracht op het deeltje als het beweegt van
![]()
aan
![]()
(b) het kiezen van een geschikt referentiepunt van de potentiële energie om nul te zijn op
![]()
zoek de potentiële energie voor deze kracht.
Toon Oplossing
![]()
het Vinden van de kracht wordt uitgeoefend overeenkomende met de potentiële energie
![]()
De potentiële energie van de functie voor een van de twee atomen in een twee-atomische molecule wordt vaak benaderd door
![]()
waarbij x de afstand tussen de atomen. (A) Op welke afstand van afscheiding heeft de potentiële energie een lokaal minimum (niet op
![]()
(b) Wat is de kracht op een atoom bij deze scheiding? (C) Hoe varieert de kracht met de scheidingsafstand?
oplossing
a tonen.
![]()
; b.
![]()
; c.
![]()
Een deeltje met massa
![]()
beweegt onder invloed van de kracht
![]()
Als de snelheid op de
![]()
is
![]()
wat is de snelheid op de
![]()
Een deeltje met massa
![]()
beweegt onder invloed van de kracht
![]()
Als de snelheid op de
![]()
is
![]()
Wat is zijn snelheid bij
![]()
oplossing tonen
![]()
een krat op rollen wordt zonder wrijvingsverlies over de vloer van een goederenwagon geduwd (zie onderstaande figuur). De auto beweegt naar rechts met een constante snelheid
![]()
als de krat in rust begint ten opzichte van de goederenwagen, dan van de werk-energiestelling,
![]()
waarbij d, de afstand die de krat beweegt, en v, De snelheid van de krat, beide worden gemeten ten opzichte van de goederenwagen. (A) aan een waarnemer in rust naast de sporen, welke afstand
![]()
wordt het krat geduwd als het de afstand d in de auto beweegt? (B) Wat zijn de begin-en eindsnelheden van de krat
![]()
en
![]()
zoals gemeten door de waarnemer naast de sporen? c) aantonen dat
![]()
en, bijgevolg, dat werk is gelijk aan de verandering in kinetische energie in beide referentiesystemen.
Woordenlijst
conservatieve krachtkracht die onafhankelijk werkt van pad exacte differentieel is het totale differentieel van een functie en vereist het gebruik van partiële afgeleiden als de functie meer dan één dimensie omvat niet-conservatieve krachtkracht die werkt die afhankelijk is van pad
Leave a Reply