Fizyka Uniwersytecka Tom 1 1
8 energia potencjalna i jej zachowanie
cele uczenia się
pod koniec tej sekcji będziesz mógł:
- scharakteryzuj siłę zachowawczą na kilka różnych sposobów
- określ warunki matematyczne, które muszą być spełnione przez siłę zachowawczą i jej składniki
- odnoś siłę zachowawczą między cząstkami układu do energii potencjalnej układu
- Oblicz składniki siły zachowawczej w różnych przypadkach
w energii potencjalnej i zachowaniu energii, każde przejście między energią kinetyczną i potencjalną oszczędzało całkowitą energię układu. To było niezależne od ścieżki, co oznacza, że możemy zaczynać i zatrzymywać się w dowolnych dwóch punktach problemu, a całkowita energia układu-kinetyczna Plus potencjał-w tych punktach są sobie równe. Jest to charakterystyczne dla siły Konserwatywnej. W poprzednim odcinku mieliśmy do czynienia z konserwatywnymi siłami, takimi jak siła grawitacji i siła sprężyny. Porównując ruch piłki nożnej w (rysunek), całkowita energia układu nigdy się nie zmienia, nawet jeśli grawitacyjna energia potencjalna piłki nożnej wzrasta, gdy piłka unosi się względem ziemi i spada z powrotem do początkowej grawitacyjnej energii potencjalnej, gdy piłkarz łapie piłkę. Siły niekonwencjonalne to siły rozpraszające, takie jak tarcie lub opór powietrza. Siły te zabierają energię z systemu w miarę postępu systemu, energię, której nie można odzyskać. Siły te są zależne od ścieżki, dlatego ważne jest, gdzie obiekt zaczyna się i zatrzymuje.
Siła Konserwatywna
praca wykonywana przez siłę konserwatywną jest niezależna od ścieżki; innymi słowy, praca wykonywana przez siłę konserwatywną jest taka sama dla każdej ścieżki łączącej dwa punkty:
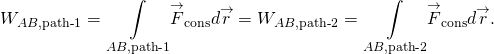
praca wykonywana przez niekonserwatywną siłę zależy od obranej ścieżki.
równoważnie, siła jest zachowawcza, jeśli praca, którą wykonuje wokół dowolnej zamkniętej ścieżki, wynosi zero:
![]()
(Figure) I (Figure) są równoważne, ponieważ każda zamknięta ścieżka jest sumą dwóch ścieżek: pierwsza idzie z A do B, a druga z B Do A. praca wykonana idąc wzdłuż ścieżki z B do A jest negatywem pracy wykonanej idącej wzdłuż tej samej ścieżki z A do B, gdzie A i B są dowolnymi dwoma punktami na zamkniętej ścieżce:
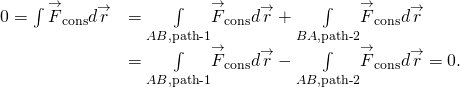
możecie zapytać, w jaki sposób udowadniamy, czy siła jest konserwatywna, ponieważ definicje obejmują wszystkie ścieżki od A do B, lub wszystkie zamknięte ścieżki, ale aby wykonać całkę dla pracy, musisz wybrać konkretną ścieżkę. Jedną z odpowiedzi jest to, że wykonywana praca jest niezależna od ścieżki, jeśli nieskończenie
![]()
jest dokładną różnicą, sposób, w jaki infinitezymalna praca sieci była równa dokładnej różnicy energii kinetycznej,
![]()
kiedy wyprowadziliśmy twierdzenie praca-energia w twierdzeniu praca-Energia. Istnieją warunki matematyczne, których można użyć do sprawdzenia, czy nieskończenie mała praca wykonywana przez siłę jest dokładną różnicą, a siła jest zachowawcza. Warunki te wiążą się tylko z różnicowaniem, a zatem są stosunkowo łatwe do zastosowania. W dwóch wymiarach, warunek dla
![]()
być dokładną różnicą jest
![]()
możesz sobie przypomnieć, że praca wykonana przez siłę w (rysunek) zależała od ścieżki. Dla tej siły,
![]()
dlatego,
![]()
co wskazuje, że jest to siła niekonserwatywna. Widzisz, co możesz zmienić, by stać się konserwatywną siłą?

przykład
konserwatywny czy nie?
które z poniższych sił dwuwymiarowych są konserwatywne, a które nie? Załóżmy, że a i b są stałymi o odpowiednich jednostkach:
(a)
![]()
(b)
![]()
(c)
![]()
Strategia
Zastosuj warunek podany w (rysunek), a mianowicie przy użyciu pochodnych składników każdej wskazanej siły. Jeśli pochodna składowej y siły względem x jest równa pochodnej składowej x siły względem y, to siła jest siłą zachowawczą, co oznacza, że droga przyjęta do obliczeń energii potencjalnej lub pracy zawsze daje takie same wyniki.
rozwiązanie
-
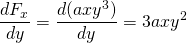
oraz
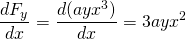
, więc ta siła nie jest konserwatywna.
-
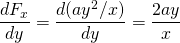
oraz
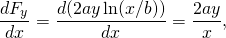
więc ta siła jest konserwatywna.
-
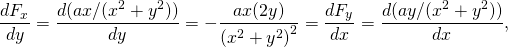
znowu konserwatywny.
Znaczenie
warunki w (rysunek) są pochodnymi jako funkcjami pojedynczej zmiennej; w trzech wymiarach istnieją podobne warunki, które obejmują więcej pochodnych.
Sprawdź swoje zrozumienie
dwuwymiarowa, zachowawcza siła jest zerowa na osiach x i y i spełnia warunek
![]()
. Jaka jest wielkość siły w punkcie
![]()
Pokaż rozwiązanie
2.83 N
przed opuszczeniem tej sekcji zauważamy, że siły niekonserwatywne nie mają energii potencjalnej z nimi związanej, ponieważ energia jest tracona do systemu i nie może być później przekształcona w użyteczną pracę. Tak więc zawsze istnieje konserwatywna Siła związana z każdą energią potencjalną. Widzieliśmy, że energia potencjalna jest definiowana w odniesieniu do pracy wykonywanej przez siły konserwatywne. Ta relacja (rysunek) obejmowała całkę dla pracy; zaczynając od siły i przesunięcia, integrujesz się, aby uzyskać pracę i zmianę energii potencjalnej. Jednak integracja jest odwrotną operacją różnicowania; równie dobrze można było zacząć od energii potencjalnej i wziąć jej pochodną, w odniesieniu do przesunięcia, aby uzyskać siłę. Infinitezymalny przyrost energii potencjalnej jest iloczynem punktowym siły i infinitezymalnego przemieszczenia,
![]()
tutaj zdecydowaliśmy się reprezentować przemieszczenie w dowolnym kierunku przez
![]()
aby nie ograniczać się do żadnego konkretnego kierunku współrzędnych. Wyraziliśmy również iloczyn punktowy w kategoriach wielkości infinitezymalnego przemieszczenia i składowej siły w jego kierunku. Obie te wielkości są skalarami, więc można podzielić przez dl, aby uzyskać
![]()
równanie to daje zależność pomiędzy siłą a związaną z nią energią potencjalną. Innymi słowy, składowa siły zachowawczej, w określonym kierunku, jest równa ujemnej pochodnej odpowiadającej jej energii potencjalnej, w odniesieniu do przesunięcia w tym kierunku. Dla ruchu jednowymiarowego, powiedzmy wzdłuż osi x, (rysunek) dać całą siłę wektora,
![]()
w dwóch wymiarach,
![]()
z tego równania można zobaczyć, dlaczego (rysunek) jest warunkiem, aby praca była dokładną różnicą, pod względem pochodnych składowych siły. Na ogół stosuje się notację pochodną cząstkową. Jeśli funkcja ma w sobie wiele zmiennych, pochodna jest pobierana tylko ze zmiennej, którą określa pochodna cząstkowa. Pozostałe zmienne są stałe. W trzech wymiarach dodajemy kolejne określenie składowej z, w wyniku czego siła jest ujemna gradientu energii potencjalnej. Nie będziemy jednak jeszcze patrzeć na trójwymiarowe przykłady.
przykład
siła spowodowana Kwartyczną energią potencjalną
energia potencjalna cząstki przechodzącej jednowymiarowy ruch wzdłuż osi x wynosi
![]()
gdzie
![]()
jego całkowita energia w
![]()
i nie podlega żadnym niekonserwatywnym siłom. Znaleźć (a) pozycje, w których jego energia kinetyczna jest zerowa oraz (b) siły w tych pozycjach.
Strategia
(A) możemy znaleźć pozycje, w których
![]()
zatem energia potencjalna jest równa całkowitej energii danego układu. (b) za pomocą (rysunek) możemy znaleźć siłę obliczoną w pozycjach znalezionych z poprzedniej części, ponieważ energia mechaniczna jest zachowana.
rozwiązanie
- energia całkowita układu 2 J równa się energii sprężystej kwartycznej podanej w problemie,

rozwiązywanie dla
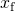
wyniki w
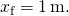
- od (rysunek),
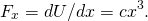
tak więc, oceniając siłę w
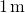
, otrzymujemy
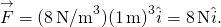
w obu pozycjach, wielkość sił wynosi 8 N, A kierunki są w kierunku początku, ponieważ jest to potencjał energia dla siły przywracającej.
Znaczenie
znalezienie siły z energii potencjalnej jest matematycznie łatwiejsze niż znalezienie energii potencjalnej z siły, ponieważ różnicowanie funkcji jest na ogół łatwiejsze niż całkowanie.
Sprawdź swoje zrozumienie
Znajdź siły na cząstkę w (rysunek), gdy jej energia kinetyczna wynosi 1.0 J at
![]()
Pokaż rozwiązanie
![]()
skierowane ku początkowi
podsumowanie
- Siła konserwatywna to taka, dla której wykonywana praca jest niezależna od ścieżki. Równoważnie, siła jest zachowawcza, jeśli praca wykonywana na dowolnej zamkniętej ścieżce wynosi zero.
- Siła niekonwencjonalna to taka, dla której wykonywana praca zależy od ścieżki.
- dla siły zachowawczej praca infinitezymalna jest dokładną różnicą. Implikuje to warunki na pochodnych składowych siły.
- składowa siły zachowawczej, w określonym kierunku, równa się ujemnej pochodnej energii potencjalnej dla tej siły, w odniesieniu do przesunięcia w tym kierunku.
pytania koncepcyjne
jakie jest fizyczne znaczenie siły niekonserwatywnej?
Pokaż rozwiązanie
Siła odbierająca energię systemowi, której nie można odzyskać, gdybyśmy mieli odwrócić akcję.
rakieta butelkowa jest wystrzelona prosto w powietrze z prędkością
![]()
. Jeśli opór powietrza zostanie zignorowany, butelka wzrośnie do wysokości około
![]()
. Rakieta idzie jednak tylko do
![]()
przed powrotem na ziemię. Co się stało? Wyjaśnij, dając tylko jakościową odpowiedź.
zewnętrzna siła działa na cząstkę podczas podróży z jednego punktu do drugiego i z powrotem do tego samego punktu. Cząstka ta jest oddziaływana tylko przez siły zachowawcze. Czy energia kinetyczna i energia potencjalna tej cząstki zmieniają się w wyniku tej podróży?
Pokaż rozwiązanie
zmiana energii kinetycznej to praca netto. Ponieważ siły zachowawcze są niezależne od ścieżki, kiedy jesteś z powrotem do tego samego punktu, Energie kinetyczne i potencjalne są dokładnie takie same jak początek. Podczas podróży całkowita energia jest zachowana, ale zmienia się zarówno energia potencjalna, jak i kinetyczna.
problemy
Siła
![]()
działa na cząstkę poruszającą się wzdłuż dodatniej osi X. a) ile pracy wykonuje siła na cząsteczce, gdy porusza się ona od
![]()
na
![]()
(b) wybranie dogodnego punktu odniesienia energii potencjalnej na zero przy
![]()
znajdź energię potencjalną dla tej siły.
Siła
![]()
działa na cząstkę. a) ile pracy wykonuje siła na cząsteczce, gdy porusza się ona od
![]()
na
![]()
(b) wybranie dogodnego punktu odniesienia energii potencjalnej na zero przy
![]()
znajdź energię potencjalną dla tej siły.
Pokaż rozwiązanie
![]()
znajdź siłę odpowiadającą energii potencjalnej
![]()
funkcja energii potencjalnej dla jednego z dwóch atomów w dwuatomowej cząsteczce jest często przybliżana przez
![]()
gdzie x jest odległością między atomami. a) w jakiej odległości od siebie energia potencjalna ma lokalne minimum (Nie w
![]()
(b) jaka jest siła na atom w tym rozdzieleniu? (c) w jaki sposób siła zmienia się w zależności od odległości separacji?
Pokaż rozwiązanie
a.
![]()
; b.
![]()
; c.
![]()
cząstka masy
![]()
porusza się pod wpływem siły
![]()
jeśli jego prędkość na
![]()
is
![]()
jaka jest jego prędkość przy
![]()
cząstka masy
![]()
porusza się pod wpływem siły
![]()
jeśli jego prędkość na
![]()
jest
![]()
jaka jest jego prędkość przy
![]()
Pokaż rozwiązanie
![]()
Skrzynia na rolkach jest pchana bez utraty energii przez tarcie po podłodze wagonu towarowego (patrz poniższy rysunek). Samochód porusza się w prawo ze stałą prędkością
![]()
jeśli skrzynia zaczyna się w spoczynku względem wagonu towarowego, to z twierdzenia o pracy-energii,
![]()
gdzie d, odległość, jaką porusza się skrzynia, I v, prędkość skrzyni, są mierzone w stosunku do wagonu towarowego. a) do obserwatora spoczywającego przy torach, jaka odległość
![]()
czy skrzynia jest pchana, gdy porusza się na odległość d w samochodzie? b) jakie są prędkości początkowe i końcowe skrzyni
![]()
oraz
![]()
mierzony przez obserwatora przy torach? C) wykazać, że
![]()
w konsekwencji praca ta jest równa zmianie energii kinetycznej w obu układach odniesienia.

Słowniczek
Siła zachowawcza siła, która działa niezależnie od ścieżki dokładna różnica jest całkowitą różnicą funkcji i wymaga użycia pochodnych cząstkowych, jeśli funkcja zawiera więcej niż jeden wymiar Siła niekonwencjonalna siła, która działa, która zależy od ścieżki
Leave a Reply