Universidade de Física de Volume 1
8 Energia Potencial e Conservação de Energia
Objetivos
no final desta seção, você será capaz de:
- Caracterizar um conservador força de várias maneiras diferentes
- Especificar as condições matemáticas que devem ser satisfeitas por uma força conservadora e seus componentes
- Relacionar o conservador força entre partículas de um sistema para a energia potencial do sistema
- Calcular os componentes de uma força conservadora em vários casos
Em Energia Potencial e Conservação da Energia, qualquer de transição entre a energia cinética e potencial conservar a energia total do sistema. Isso era independente do caminho, o que significa que podemos começar e parar em dois pontos no problema, e a energia total do sistema—cinética mais potencial—nesses pontos são iguais entre si. Isso é característico de uma força conservadora. Lidamos com forças conservadoras na seção anterior, como a força gravitacional e a força da mola. Ao comparar o movimento do futebol em (Figura), a energia total do sistema nunca muda, embora a energia potencial gravitacional do futebol aumente, à medida que a bola sobe em relação ao solo e volta à energia potencial gravitacional inicial quando o jogador de futebol pega a bola. Forças não conservadoras são forças dissipativas, como fricção ou resistência ao ar. Essas forças tiram energia do sistema à medida que o sistema progride, energia que você não pode recuperar. Essas forças dependem do caminho; portanto, importa onde o objeto começa e para.
Conservador Força
O trabalho realizado por uma força conservadora é independente do caminho; em outras palavras, o trabalho realizado por uma força conservadora é a mesma para qualquer caminho ligando dois pontos:
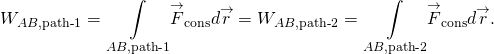
O trabalho feito por um não-conservador força depende do caminho percorrido.
Equivalentemente, uma força conservadora, se o trabalho que ele faz em torno de qualquer caminho fechado é zero:
![]()
(a Figura) e (Figura) são equivalentes porque qualquer caminho fechado é a soma dos dois caminhos: o primeiro vai de a para B, e a segunda vai de B para A. O trabalho feito indo ao longo de um caminho de B para Um é o negativo do trabalho realizado percorrendo o mesmo caminho de a a B, onde A e B são dois pontos quaisquer a caminho fechado:
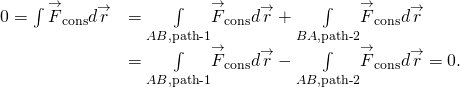
Você deve se perguntar como vamos provar a existência ou não de uma força conservadora, desde as definições envolvem qualquer e todos os caminhos de a a B, ou qualquer e todos os caminhos fechados, mas para fazer a integral para o trabalho, você tem que escolher um determinado caminho. Uma resposta é que o trabalho feito é independente do caminho, se o trabalho infinitesimal
![]()
é uma diferencial exata, a forma como o infinitesimal trabalho da rede, que era igual ao diferencial exata da energia cinética,
![]()
quando nós derivada do trabalho-energia, teorema Trabalho-Energia Teorema. Existem condições matemáticas que você pode usar para testar se o trabalho infinitesimal feito por uma força é um diferencial exato e a força é conservadora. Essas condições envolvem apenas diferenciação e, portanto, são relativamente fáceis de aplicar. Em duas dimensões, a condição para
![]()
para ser um diferencial exata é
![]()
Você pode recordar que o trabalho realizado pela força (da Figura) dependia do caminho. Para que a força,
![]()
Portanto,,
![]()
o que indica que ele é um não-conservador força. Você pode ver o que você poderia mudar para torná-lo uma força conservadora?

Exemplo
Conservador ou Não?
Qual das seguintes forças bidimensionais são conservadoras e quais não são? Suponha que a e b sejam constantes com unidades apropriadas:
(a)
![]()
(b)
![]()
(c)
![]()
Estratégia
Aplicar a condição de indicado na (Figura), ou seja, usando as derivadas das componentes de cada força indicada. Se a derivada do componente y da força em relação a x for igual à derivada do componente x da força em relação a y, a força é uma força conservadora, o que significa que o caminho percorrido para cálculos de energia potencial ou Trabalho sempre produz os mesmos resultados.
Solução
-
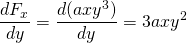
e
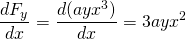
, então, esta força é não-conservador.
-
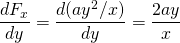
e
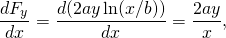
então, esta força é conservador.
-
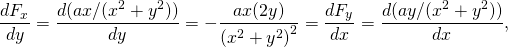
novamente conservador.
significância
as condições em (Figura) são derivadas como funções de uma única variável; em três dimensões, existem condições semelhantes que envolvem mais derivadas.
Verificar a Sua Compreensão
Um bidimensional, conservador força é zero em x e y-eixos, e satisfaz a condição
![]()
. Qual é a magnitude da força no ponto
![]()
Mostrar a Solução
2.83 N
Antes de deixar esta seção, nota-se que não forças conservadoras não têm energia potencial associada a eles, porque a energia é perdida para o sistema e não pode ser transformada em trabalho útil mais tarde. Portanto, há sempre uma força conservadora associada a todas as energias potenciais. Vimos que a energia potencial é definida em relação ao trabalho realizado por forças conservadoras. Essa relação, (figura), envolveu uma integral para o trabalho; começando com a força e o deslocamento, você se integrou para obter o trabalho e a mudança na energia potencial. No entanto, a integração é a operação inversa da diferenciação; você poderia igualmente bem ter começado com a energia potencial e tomado sua derivada, em relação ao deslocamento, para obter a força. O incremento infinitesimal de energia potencial é o produto escalar da força e o deslocamento infinitesimal,
![]()
Aqui, optou-se por representar o deslocamento em uma direção arbitrária por
![]()
para não estar limitado a um determinado coordenar direção. Também expressamos o produto pontual em termos da magnitude do deslocamento infinitesimal e do componente da força em sua direção. Estas duas quantidades são escalares, então você pode dividir pelo dl para obter
![]()
Esta equação fornece a relação entre a força e a energia potencial associada a ele. Em palavras, o componente de uma força conservadora, em uma direção particular, é igual ao negativo da derivada da energia potencial correspondente, em relação a um deslocamento nessa direção. Para uma dimensão do movimento, diga ao longo do eixo x, (Figura a) dar todo o vetor de força,
![]()
Em duas dimensões,
![]()
a Partir desta equação, pode-se ver por (Figura) é a condição para que o trabalho seja uma diferencial exata, em termos das derivadas das componentes da força. Em geral, uma notação derivada parcial é usada. Se uma função tem muitas variáveis, a derivada é tomada apenas da variável que a derivada parcial especifica. As outras variáveis são mantidas constantes. Em três dimensões, você adiciona outro termo para o componente z, e o resultado é que a força é o negativo do gradiente da energia potencial. No entanto, ainda não veremos exemplos tridimensionais.
Exemplo
Força devido a uma Quártica Potencial de Energia
A energia potencial de uma partícula submetidos a uma dimensão de movimento ao longo do eixo x é
![]()
onde
![]()
o Seu total de energia no
![]()
e não está sujeita a qualquer não-forças conservadoras. Encontre (a) as posições onde sua energia cinética é zero e (b) as forças nessas posições.
Estratégia
(a) podemos encontrar as posições onde
![]()
assim, a energia potencial é igual a energia total do sistema. (b) usando (figura), podemos encontrar a força avaliada nas posições encontradas na parte anterior, uma vez que a energia mecânica é conservada.
Solução
- A energia total do sistema, de 2 de J é igual a quártica energia elástica como dado no problema,

a Solução para
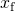
resultados
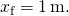
- a Partir de (Figura),
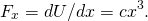
Assim, avaliar a força
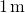
, temos
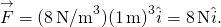
Em ambas as posições, a magnitude da força é de 8 N e as direções são para a origem, pois este é o potencial energia para uma força restauradora.
Significância
Encontrar a força da energia potencial é matematicamente mais fácil do que encontrar a energia potencial da força, porque a diferenciação de uma função é geralmente mais fácil do que a integração de um.
verifique sua compreensão
Encontre as forças na partícula em (figura) quando sua energia cinética é 1.0 J no
![]()
Mostrar a Solução
![]()
voltada para a origem,
Resumo
- Uma força conservadora é aquela para a qual o trabalho feito é independente do caminho. Equivalentemente, uma força é conservadora se o trabalho realizado em qualquer caminho fechado for zero.
- uma força não conservadora é aquela para a qual o trabalho realizado depende do caminho.
- para uma força conservadora, o trabalho infinitesimal é um diferencial exato. Isso implica Condições sobre os derivados dos componentes da força.
- o componente de uma força conservadora, em uma direção particular, é igual ao negativo da derivada da energia potencial para essa força, em relação a um deslocamento nessa direção.
questões conceituais
Qual é o significado físico de uma força não conservadora?
Mostrar solução
uma força que tira energia do sistema que não pode ser recuperada se quisermos reverter a ação.
Um foguete é disparada no ar com uma velocidade de
![]()
. Se a resistência do ar for ignorada, a garrafa subiria a uma altura de aproximadamente
![]()
. No entanto, o foguete sobe apenas para
![]()
antes de voltar ao chão. O que houve? Explique, dando apenas uma resposta qualitativa.
uma força externa atua sobre uma partícula durante uma viagem de um ponto a outro e de volta a esse mesmo ponto. Esta partícula só é efetuada por forças conservadoras. A energia cinética e a energia potencial dessa partícula mudam como resultado dessa viagem?
Mostrar solução
a mudança na energia cinética é o trabalho líquido. Como as forças conservadoras são independentes do caminho, quando você está de volta ao mesmo ponto, as energias cinética e potencial são exatamente as mesmas do começo. Durante a viagem, a energia total é conservada, mas tanto o potencial quanto a energia cinética mudam.
Problemas
Uma força
![]()
atua sobre uma partícula, como ele se move no lado positivo do eixo x. (a) Quanto trabalho a força sobre a partícula, como ele se move de
![]()
para
![]()
(b) escolher um conveniente ponto de referência da energia potencial como sendo zero no
![]()
encontrar a energia potencial para esta força.
Uma força
![]()
atua sobre uma partícula. (a) Quanto trabalho a força sobre a partícula, como ele se move de
![]()
para
![]()
(b) escolher um conveniente ponto de referência da energia potencial como sendo zero no
![]()
encontrar a energia potencial para esta força.
Mostrar a Solução
![]()
Encontrar a força correspondente à energia potencial
![]()
A energia potencial de função para qualquer um dos dois átomos em moléculas de molécula é frequentemente abordada por
![]()
onde x é a distância entre os átomos. (a) A que distância de separação a energia potencial tem um mínimo local (não em
![]()
(b) Qual é a força em um átomo a esta separação? (c) como a força varia com a distância de separação?
Mostrar a Solução
um.
![]()
; b.
![]()
; c.
![]()
Uma partícula de massa
![]()
move sob a influência da força
![]()
Se a sua velocidade em
![]()
é
![]()
qual é a sua velocidade em
![]()
Uma partícula de massa
![]()
move sob a influência da força
![]()
Se a sua velocidade em
![]()
é
![]()
qual é a sua velocidade em
![]()
Mostrar a Solução
![]()
Um caixote sobre rodas está sendo empurrado sem atrito, perda de energia em todo o andar de um carro de frete (veja figura a seguir). O carro está se movendo para a direita com uma velocidade constante
![]()
Se a caixa começa em repouso em relação ao vagão, em seguida, a partir do trabalho-energia teorema,
![]()
onde d, a distância que o caixote se desloca, e v, a velocidade do caixote, são ambos medidos em relação ao carro de frete. (a) a um observador em repouso ao lado dos trilhos, que distância
![]()
a caixa é empurrada quando move a distância d no carro? (b) Quais a caixa inicial e final do velocidades
![]()
e
![]()
como medido pelo observador ao lado dos trilhos? C) mostrar que
![]()
e, consequentemente, esse trabalho é igual à mudança na energia cinética em ambos os sistemas de referência.

Glossário
conservador-de-obra, que funciona independente do caminho exato diferencial é o diferencial total de uma função e requer o uso de derivadas parciais se a função envolve mais do que uma dimensão não-conservador-de-obra que faz um trabalho que depende do caminho
Leave a Reply