volumul fizicii universitare 1
8 energia potențială și conservarea energiei
obiective de învățare
până la sfârșitul acestei secțiuni, veți putea:
- caracterizați o forță conservatoare în mai multe moduri diferite
- specificați condițiile matematice care trebuie îndeplinite de o forță conservatoare și componentele sale
- raportați forța conservatoare dintre particulele unui sistem la energia potențială a sistemului
- calculați componentele unei forțe conservatoare în diferite cazuri
în energia potențială și conservarea energiei, orice tranziție între energia cinetică și energia potențială a conservat energia totală a sistemului. Aceasta a fost o cale independentă, ceea ce înseamnă că putem porni și opri în oricare două puncte ale problemei, iar energia totală a sistemului—potențialul cinetic plus—în aceste puncte sunt egale între ele. Acest lucru este caracteristic unei forțe conservatoare. Ne-am ocupat de forțe conservatoare în secțiunea precedentă, cum ar fi forța gravitațională și forța arcului. Atunci când se compară mișcarea fotbalului în (figura), energia totală a sistemului nu se schimbă niciodată, chiar dacă energia potențială gravitațională a fotbalului crește, pe măsură ce mingea se ridică în raport cu solul și cade înapoi la energia potențială gravitațională inițială atunci când jucătorul de fotbal prinde mingea. Forțele neconservatoare sunt forțe disipative, cum ar fi fricțiunea sau rezistența la aer. Aceste forțe iau energie din sistem pe măsură ce sistemul progresează, energie pe care nu o puteți obține înapoi. Aceste forțe sunt dependente de cale; prin urmare, contează unde începe și se oprește obiectul.
forța conservatoare
munca făcută de o forță conservatoare este independentă de cale; cu alte cuvinte, munca făcută de o forță conservatoare este aceeași pentru orice cale care leagă două puncte:
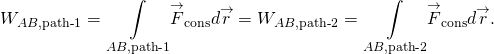
munca depusă de o forță neconservatoare depinde de calea luată.
echivalent, o forță este conservatoare dacă munca pe care o face în jurul oricărei căi închise este zero:
![]()
(figura) și (figura) sunt echivalente deoarece orice cale închisă este suma a două căi: primul merge de la A la B, iar al doilea merge de la B La A. lucrarea făcută mergând de-a lungul unei căi de la B la A este negativul lucrării efectuate mergând de-a lungul aceleiași căi de la A la B, unde A și B sunt oricare două puncte pe calea închisă:
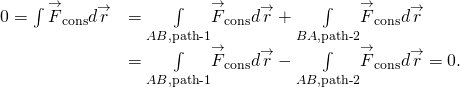
s-ar putea să vă întrebați cum vom dovedi dacă o forță este sau nu conservatoare, deoarece definițiile implică oricare și toate căile de la A la B sau oricare și toate căile închise, dar pentru a face integrala pentru lucrare, trebuie să alegeți o anumită cale. Un răspuns este că munca făcută este independentă de cale dacă lucrarea infinitezimală
![]()
este un diferențial exact, modul în care munca netă infinitezimală a fost egală cu diferențialul exact al energiei cinetice,
![]()
când am derivat teorema muncii-energie în teorema muncii-energie. Există condiții matematice pe care le puteți utiliza pentru a testa dacă munca infinitezimală efectuată de o forță este un diferențial exact, iar forța este conservatoare. Aceste condiții implică doar diferențierea și, prin urmare, sunt relativ ușor de aplicat. În două dimensiuni, condiția pentru
![]()
pentru a fi un diferențial exact este
![]()
vă puteți aminti că munca făcută de forța din (Figura) depindea de cale. Pentru acea forță,
![]()
prin urmare,
![]()
ceea ce indică faptul că este o forță non-conservatoare. Puteți vedea ce ați putea schimba pentru a face o forță conservatoare?

exemplu
conservator sau nu?
care dintre următoarele forțe bidimensionale sunt conservatoare și care nu sunt? Să presupunem că a și b sunt constante cu unități adecvate:
(a)
![]()
(b)
![]()
(c)
![]()
strategia
aplică condiția menționată în (figura), și anume, folosind derivatele componentelor fiecărei forțe indicate. Dacă derivata componentei y a forței în raport cu x este egală cu derivata componentei x a forței în raport cu y, forța este o forță conservatoare, ceea ce înseamnă că calea luată pentru energia potențială sau calculele de lucru dă întotdeauna aceleași rezultate.
soluție
-
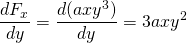
și
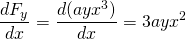
, deci, această forță este non-conservatoare.
-
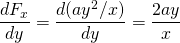
și
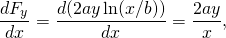
deci această forță este conservatoare.
-
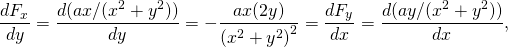
din nou conservator.
semnificație
condițiile din (figura) sunt derivate ca funcții ale unei singure variabile; în trei dimensiuni, există condiții similare care implică mai multe derivate.
verificați-vă înțelegerea
o forță bidimensională, conservatoare este zero pe axele x și y și satisface condiția
![]()
. Care este magnitudinea forței la punctul
![]()
arată soluție
2.83 N
înainte de a părăsi această secțiune, observăm că forțele non-conservatoare nu au energie potențială asociată cu ele, deoarece energia este pierdută în sistem și nu poate fi transformată în muncă utilă mai târziu. Deci, există întotdeauna o forță conservatoare asociată cu fiecare energie potențială. Am văzut că energia potențială este definită în raport cu munca depusă de forțele conservatoare. Această relație, (Figura), a implicat o integrală pentru muncă; începând cu forța și deplasarea, v-ați integrat pentru a obține munca și schimbarea energiei potențiale. Cu toate acestea, integrarea este operația inversă a diferențierii; la fel de bine ați fi putut începe cu energia potențială și ați luat derivata sa, în ceea ce privește deplasarea, pentru a obține forța. Creșterea infinitesimală a energiei potențiale este produsul punct al forței și al deplasării infinitesimale,
![]()
aici, am ales să reprezentăm deplasarea într-o direcție arbitrară prin
![]()
pentru a nu fi limitat la o anumită direcție de coordonate. De asemenea, am exprimat produsul punct în ceea ce privește magnitudinea deplasării infinitesimale și componenta forței în direcția sa. Ambele cantități sunt scalare, astfel încât să puteți împărți cu dl pentru a obține
![]()
această ecuație dă relația dintre forță și energia potențială asociată cu ea. În cuvinte, componenta unei forțe conservatoare, într-o anumită direcție, este egală cu negativul derivatului energiei potențiale corespunzătoare, în raport cu o deplasare în acea direcție. Pentru mișcarea unidimensională, spuneți de-a lungul axei x, (figura) dați întreaga forță vectorială,
![]()
în două dimensiuni,
![]()
din această ecuație, puteți vedea de ce (figura) este condiția ca lucrarea să fie un diferențial exact, în ceea ce privește derivatele componentelor forței. În general, se utilizează o notație derivată parțială. Dacă o funcție are multe variabile în ea, derivata este luată numai din variabila specifică derivata parțială. Celelalte variabile sunt menținute constante. În trei dimensiuni, adăugați un alt termen pentru componenta z, iar rezultatul este că forța este negativul gradientului energiei potențiale. Cu toate acestea, nu vom analiza încă Exemple tridimensionale.
exemplu
forța datorată unei energii potențiale Quartice
energia potențială pentru o particulă care suferă o mișcare unidimensională de-a lungul axei X este
![]()
unde
![]()
energia sa totală la
![]()
și nu este supusă nici unei forțe non-conservatoare. Găsiți (a) pozițiile în care energia sa cinetică este zero și (b) forțele din acele poziții.
strategie
(a) putem găsi pozițiile în care
![]()
deci energia potențială este egală cu energia totală a sistemului dat. (b) folosind (figura), putem găsi forța evaluată la pozițiile găsite din partea anterioară, deoarece energia mecanică este conservată.
soluție
- energia totală a sistemului de 2 J este egală cu energia elastică quartică dată în problemă,

rezolvarea pentru
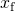
rezultate în
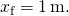
- din (Figura),
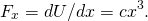
astfel, evaluarea forței la
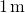
, obținem
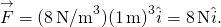
în ambele poziții, magnitudinea forțelor este de 8 N și direcțiile sunt spre origine, deoarece acesta este potențialul energie pentru o forță de restaurare.
semnificație
găsirea Forței din energia potențială este matematic mai ușoară decât găsirea energiei potențiale din forță, deoarece diferențierea unei funcții este în general mai ușoară decât integrarea uneia.
verificați-vă înțelegerea
găsiți forțele asupra particulei în (figura) când energia sa cinetică este 1.0 J la
![]()
afișează soluția
![]()
îndreptată spre origine
rezumat
- o forță conservatoare este una pentru care munca depusă este independentă de cale. Echivalent, o forță este conservatoare dacă munca depusă pe orice cale închisă este zero.
- o forță neconservatoare este una pentru care munca depusă depinde de cale.
- pentru o forță conservatoare, lucrarea infinitezimală este un diferențial exact. Aceasta implică condiții privind derivatele componentelor forței.
- componenta unei forțe conservatoare, într-o anumită direcție, este egală cu negativul derivatei energiei potențiale pentru acea forță, în raport cu o deplasare în acea direcție.
întrebări conceptuale
care este sensul fizic al unei forțe neconservatoare?
arată soluție
o forță care ia energie departe de sistem care nu poate fi recuperată dacă ar fi să inversăm acțiunea.
o rachetă de sticlă este împușcată direct în aer cu o viteză
![]()
. Dacă rezistența aerului este ignorată, sticla ar merge până la o înălțime de aproximativ
![]()
. Cu toate acestea, racheta merge până la numai
![]()
înainte de a reveni la pământ. Ce s-a întâmplat? Explicați, oferind doar un răspuns calitativ.
o forță externă acționează asupra unei particule în timpul unei călătorii dintr-un punct în altul și înapoi în același punct. Această particulă este efectuată numai de forțele conservatoare. Energia cinetică și energia potențială a acestei particule se schimbă ca urmare a acestei călătorii?
Afișați soluția
schimbarea energiei cinetice este lucrarea netă. Deoarece forțele conservatoare sunt independente de cale, atunci când vă întoarceți în același punct, energiile cinetice și potențiale sunt exact aceleași cu începutul. În timpul călătoriei, energia totală este conservată, dar atât energia potențială, cât și cea cinetică se schimbă.
probleme
o forță
![]()
acționează asupra unei particule în timp ce se deplasează de-a lungul axei X pozitive. (a) cât de mult lucrează forța asupra particulei pe măsură ce se deplasează de la
![]()
la
![]()
(B) alegerea unui punct de referință convenabil al energiei potențiale care să fie zero la
![]()
găsiți energia potențială pentru această forță.
o forță
![]()
acționează asupra unei particule. (a) cât de mult lucrează forța asupra particulei pe măsură ce se deplasează de la
![]()
la
![]()
(B) alegerea unui punct de referință convenabil al energiei potențiale care să fie zero la
![]()
găsiți energia potențială pentru această forță.
afișează soluția
![]()
găsiți forța corespunzătoare energiei potențiale
![]()
funcția de energie potențială pentru oricare dintre cei doi atomi dintr – o moleculă diatomică este adesea aproximată de
![]()
unde x este distanța dintre atomi. (a) la ce distanță de separare are energia potențială un minim local (nu la
![]()
(b) care este forța asupra unui atom la această separare? c) cum variază forța în funcție de Distanța de separare?
afișează soluția
a.
![]()
; b.
![]()
; c.
![]()
o particulă de masă
![]()
se mișcă sub influența forței
![]()
dacă viteza sa la
![]()
este
![]()
care este viteza sa la
![]()
o particulă de masă
![]()
se mișcă sub influența forței
![]()
dacă viteza sa la
![]()
este
![]()
care este viteza sa la
![]()
afișează soluția
![]()
o ladă pe role este împinsă fără pierderi de energie prin frecare pe podeaua unei mașini de marfă (a se vedea figura următoare). Mașina se deplasează spre dreapta cu o viteză constantă
![]()
dacă Lada începe în repaus în raport cu mașina de marfă, atunci din teorema energiei de lucru,
![]()
unde d, Distanța pe care se mișcă Lada și v, Viteza cutiei, sunt ambele măsurate în raport cu vagonul de marfă. (a) unui observator în repaus lângă șine, ce distanță
![]()
cutia este împinsă atunci când deplasează distanța d în mașină? (b) care sunt vitezele inițiale și finale ale cutiei
![]()
și
![]()
măsurată de observatorul de lângă șine? (c) arată că
![]()
și, în consecință, această muncă este egală cu schimbarea energiei cinetice în ambele sisteme de referință.

Glosar
forța de forță conservatoare care funcționează independent de calea diferențială exactă este diferențialul total al unei funcții și necesită utilizarea derivatelor parțiale dacă funcția implică mai mult de o dimensiune forță de forță neconservatoare care funcționează care depinde de calea
Leave a Reply