Universitetsfysikvolym 1
8 potentiell energi och bevarande av energi
inlärningsmål
i slutet av detta avsnitt kommer du att kunna:
- karakterisera en konservativ kraft på flera olika sätt
- ange matematiska förhållanden som måste uppfyllas av en konservativ kraft och dess komponenter
- relatera den konservativa kraften mellan partiklar i ett system till systemets potentiella energi
- beräkna komponenterna i en konservativ kraft i olika fall
i potentiell energi och bevarande av energi, varje övergång mellan kinetisk och potentiell energi bevarade systemets totala energi. Detta var väg oberoende, vilket innebär att vi kan starta och stoppa vid två punkter i problemet, och den totala energin i systemet—kinetic plus potential—vid dessa punkter är lika med varandra. Detta är karakteristiskt för en konservativ kraft. Vi behandlade konservativa krafter i föregående avsnitt, såsom gravitationskraften och fjäderkraften. När man jämför fotbollens rörelse i (Figur) förändras systemets totala energi aldrig, även om fotbollens gravitationspotentialenergi ökar, när bollen stiger i förhållande till marken och faller tillbaka till den ursprungliga gravitationspotentialenergin när fotbollsspelaren fångar bollen. Icke-konservativa krafter är dissipativa krafter som friktion eller luftmotstånd. Dessa krafter tar energi bort från systemet när systemet fortskrider, energi som du inte kan få tillbaka. Dessa krafter är vägberoende; därför spelar det roll var objektet börjar och stannar.
konservativ kraft
arbetet som utförs av en konservativ kraft är oberoende av vägen; med andra ord är arbetet som utförs av en konservativ kraft detsamma för alla vägar som förbinder två punkter:
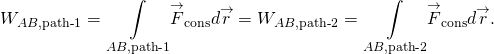
arbetet som utförs av en icke-konservativ kraft beror på den väg som tagits.
likvärdigt är en kraft konservativ om arbetet det gör runt någon stängd väg är noll:
![]()
(figur) och (figur) är ekvivalenta eftersom varje sluten väg är summan av två vägar: den första går från A till B, och den andra går från B till A. Det arbete som utförs längs en väg från B till A är det negativa av det arbete som utförs längs samma väg från A till B, där A och B är två punkter på den stängda vägen:
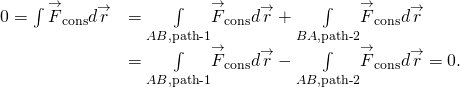
du kanske frågar hur vi ska bevisa huruvida en kraft är konservativ eller inte, eftersom definitionerna involverar alla vägar från A till B eller alla stängda vägar, men för att göra integralet för arbetet måste du välja en viss väg. Ett svar är att arbetet är oberoende av vägen om det oändliga arbetet
![]()
är en exakt skillnad, hur det oändliga nätet var lika med den exakta skillnaden mellan den kinetiska energin,
![]()
när vi härledde work-energy theorem i Work-Energy Theorem. Det finns matematiska förhållanden som du kan använda för att testa om det oändliga arbetet som utförs av en kraft är en exakt skillnad, och kraften är konservativ. Dessa villkor innebär endast differentiering och är således relativt lätta att tillämpa. I två dimensioner, villkoret för
![]()
att vara en exakt skillnad är
![]()
du kanske kommer ihåg att arbetet som utfördes av kraften i (Figur) berodde på vägen. För den kraften,
![]()
därför,
![]()
vilket tyder på att det är en icke-konservativ kraft. Kan du se vad du kan ändra för att göra det till en konservativ kraft?

exempel
konservativ eller inte?
vilka av följande tvådimensionella krafter är konservativa och vilka inte? Antag att a och b är konstanter med lämpliga enheter:
(a)
![]()
(b)
![]()
(c)
![]()
strategi
tillämpa det villkor som anges i (Figur), nämligen att använda derivaten av komponenterna i varje angiven kraft. Om derivatet av kraftens y-komponent med avseende på x är lika med derivatet av kraftens x-komponent med avseende på y, är kraften en konservativ kraft, vilket innebär att den väg som tas för potentiell energi eller arbetsberäkningar alltid ger samma resultat.
lösning
-
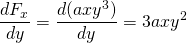
och
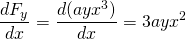
, så denna kraft är icke-konservativ.
-
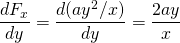
och
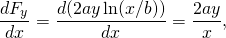
så denna kraft är konservativ.
-
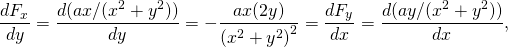
återigen konservativ.
betydelse
villkoren i (figur) är derivat som funktioner för en enda variabel; i tre dimensioner finns liknande förhållanden som involverar fler derivat.
kontrollera din förståelse
en tvådimensionell, konservativ kraft är noll på x – och y-axlarna och uppfyller villkoret
![]()
. Vad är storleken på kraften vid punkten
![]()
Visa lösning
2.83 N
innan vi lämnar detta avsnitt noterar vi att icke-konservativa krafter inte har potentiell energi associerad med dem eftersom energin går förlorad för systemet och inte kan omvandlas till användbart arbete senare. Så det finns alltid en konservativ kraft i samband med varje potentiell energi. Vi har sett att potentiell energi definieras i förhållande till det arbete som utförs av konservativa krafter. Det förhållandet, (figur), involverade en integral för arbetet; börjar med kraften och förskjutningen, du integrerade för att få arbetet och förändringen i potentiell energi. Men integration är den inversa funktionen av differentiering; du kunde lika bra ha börjat med den potentiella energin och tagit sitt derivat, med avseende på förskjutning, för att få kraften. Den oändliga ökningen av potentiell energi är punktprodukten av kraften och den oändliga förskjutningen,
![]()
här valde vi att representera förskjutningen i godtycklig riktning genom att
![]()
för att inte begränsas till någon särskild koordinatriktning. Vi uttryckte också punktprodukten när det gäller storleken på den oändliga förskjutningen och komponenten av kraften i dess riktning. Båda dessa kvantiteter är skalärer, så du kan dela med dl för att få
![]()
denna ekvation ger förhållandet mellan kraft och den potentiella energi som är associerad med den. I ord är komponenten av en konservativ kraft, i en viss riktning, lika med negativet av derivatet av motsvarande potentiell energi, med avseende på en förskjutning i den riktningen. För endimensionell rörelse, säg längs x-axeln, (figur) ge hela vektorkraften,
![]()
i två dimensioner,
![]()
från denna ekvation kan du se varför (figur) är villkoret för att arbetet ska vara en exakt skillnad, vad gäller derivaten av kraftens komponenter. I allmänhet används en partiell derivatnotation. Om en funktion har många variabler i sig tas derivatet endast av variabeln som det partiella derivatet anger. De andra variablerna hålls konstanta. I tre dimensioner lägger du till en annan term för z-komponenten, och resultatet är att kraften är den negativa av gradienten för den potentiella energin. Vi kommer dock inte att titta på tredimensionella exempel ännu.
exempel
kraft på grund av en Kvartisk potentiell energi
den potentiella energin för en partikel som genomgår endimensionell rörelse längs x-axeln är
![]()
där
![]()
dess totala energi vid
![]()
och det är inte föremål för några icke-konservativa krafter. Hitta (A) positionerna där dess kinetiska energi är noll och (b) krafterna vid dessa positioner.
strategi
(a) vi kan hitta positionerna där
![]()
så den potentiella energin är lika med den totala energin i det givna systemet. (b) med hjälp av (figur) kan vi hitta kraften utvärderad vid de positioner som hittades från föregående del, eftersom den mekaniska energin bevaras.
lösning
- systemets totala energi på 2 J är lika med den kvartiska elastiska energin som anges i problemet,

lösa för
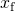
resultat i
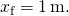
- från (Figur),
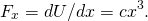
således utvärderar kraften vid
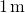
, vi får
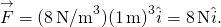
vid båda positionerna är krafternas storlek 8 N och riktningarna är mot ursprunget, eftersom detta är potentialen energi för en återställande kraft.
betydelse
att hitta kraften från den potentiella energin är matematiskt lättare än att hitta den potentiella energin från kraften, eftersom differentiering av en funktion i allmänhet är lättare än att integrera en.
kontrollera din förståelse
hitta krafterna på partikeln i (figur) när dess kinetiska energi är 1.0 J vid
![]()
Visa lösning
![]()
riktad mot ursprunget
sammanfattning
- en konservativ kraft är en för vilken arbetet är oberoende av väg. Likvärdigt är en kraft konservativ om arbetet som utförs över någon stängd väg är noll.
- en icke-konservativ kraft är en för vilken arbetet beror på vägen.
- för en konservativ kraft är det oändliga arbetet en exakt skillnad. Detta innebär villkor för derivat av kraftens komponenter.
- komponenten i en konservativ kraft, i en viss riktning, är lika med negativet av derivatet av den potentiella energin för den kraften, med avseende på en förskjutning i den riktningen.
konceptuella frågor
vad är den fysiska betydelsen av en icke-konservativ kraft?
Visa lösning
en kraft som tar energi bort från systemet som inte kan återvinnas om vi skulle vända åtgärden.
en flaska raket skjuts rakt upp i luften med en hastighet
![]()
. Om luftmotståndet ignoreras, flaskan skulle gå upp till en höjd av ungefär
![]()
. Men raketen går upp till bara
![]()
innan du återvänder till marken. Vad var det som hände? Förklara, vilket bara ger ett kvalitativt svar.
en yttre kraft verkar på en partikel under en resa från en punkt till en annan och tillbaka till samma punkt. Denna partikel utförs endast av konservativa krafter. Förändras denna partikels kinetiska energi och potentiella energi som ett resultat av denna resa?
Visa lösning
förändringen i kinetisk energi är nätet. Eftersom konservativa krafter är vägoberoende, när du är tillbaka till samma punkt är de kinetiska och potentiella energierna exakt samma som början. Under resan bevaras den totala energin, men både potential och kinetisk energi förändras.
problem
en kraft
![]()
verkar på en partikel när den rör sig längs den positiva x-axeln. (a) hur mycket arbete gör kraften på partikeln när den rör sig från
![]()
till
![]()
(B) plocka en lämplig referenspunkt för den potentiella energin att vara noll vid
![]()
hitta den potentiella energin för denna kraft.
en kraft
![]()
verkar på en partikel. (a) hur mycket arbete gör kraften på partikeln när den rör sig från
![]()
till
![]()
(B) plocka en lämplig referenspunkt för den potentiella energin att vara noll vid
![]()
hitta den potentiella energin för denna kraft.
Visa lösning
![]()
hitta kraften som motsvarar den potentiella energin
![]()
den potentiella energifunktionen för någon av de två atomerna i en diatomisk molekyl approximeras ofta av
![]()
där x är avståndet mellan atomerna. (a) på vilket avstånd av separation har den potentiella energin ett lokalt minimum (inte vid
![]()
(b) Vad är kraften på en atom vid denna separation? (c) Hur varierar kraften med separationsavståndet?
Visa lösning
a.
![]()
; b.
![]()
; c.
![]()
en partikel av massa
![]()
rör sig under påverkan av kraften
![]()
om dess hastighet vid
![]()
är
![]()
vad är dess hastighet vid
![]()
en partikel av massa
![]()
rör sig under påverkan av kraften
![]()
om dess hastighet vid
![]()
är
![]()
vad är dess hastighet vid
![]()
Visa lösning
![]()
en låda på rullar skjuts utan friktionsförlust av energi över golvet i en godsvagn (se följande figur). Bilen rör sig till höger med konstant hastighet
![]()
om kassen börjar vila i förhållande till godsbilen, då från arbetsenergisatsen,
![]()
där d, avståndet lådan rör sig, och v, hastigheten på lådan, båda mäts i förhållande till godsvagnen. (A) till en observatör i vila bredvid spåren, vilket avstånd
![]()
är lådan tryckt när den rör sig Avståndet d i bilen? (B) vilka är lådans initiala och slutliga hastigheter
![]()
och
![]()
mätt av observatören bredvid spåren? C) visa att
![]()
och följaktligen är det arbetet lika med förändringen i kinetisk energi i båda referenssystemen.
ordlista
konservativ kraftkraft som fungerar oberoende av sökväg exakt differential är den totala skillnaden för en funktion och kräver användning av partiella derivat om funktionen involverar mer än en dimension icke-konservativ kraftkraft som fungerar som beror på sökväg
Leave a Reply