Volumen de Física Universitaria 1
8 Energía potencial y Conservación de la Energía
Objetivos de aprendizaje
Al final de esta sección, podrá::
- Caracterizar una fuerza conservadora de varias maneras
- Especificar las condiciones matemáticas que debe satisfacer una fuerza conservadora y sus componentes
- Relacionar la fuerza conservadora entre partículas de un sistema con la energía potencial del sistema
- Calcular los componentes de una fuerza conservadora en varios casos
En Energía Potencial y Conservación de Energía, cualquier transición entre energía cinética y energía potencial conserva la energía total del sistema. Esto era independiente de la trayectoria, lo que significa que podemos comenzar y parar en dos puntos cualesquiera del problema, y la energía total del sistema, cinética más potencial, en estos puntos son iguales entre sí. Esto es característico de una fuerza conservadora. En la sección anterior tratamos las fuerzas conservadoras, como la fuerza gravitacional y la fuerza de resorte. Al comparar el movimiento del balón en (Figura), la energía total del sistema nunca cambia, a pesar de que la energía potencial gravitacional del balón aumenta, a medida que el balón se eleva en relación con el suelo y vuelve a la energía potencial gravitacional inicial cuando el jugador de fútbol atrapa el balón. Las fuerzas no conservadoras son fuerzas disipativas, como la fricción o la resistencia al aire. Estas fuerzas quitan energía del sistema a medida que el sistema progresa, energía que no se puede recuperar. Estas fuerzas dependen de la trayectoria; por lo tanto, importa dónde comienza y se detiene el objeto.
Fuerza conservadora
El trabajo realizado por una fuerza conservadora es independiente del camino; en otras palabras, el trabajo realizado por una fuerza conservadora es el mismo para cualquier camino que conecte dos puntos:
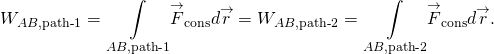
El trabajo realizado por una fuerza no conservadora depende del camino que se tome.
De forma equivalente, una fuerza es conservadora si el trabajo que realiza alrededor de cualquier camino cerrado es cero:
![]()
(Figura) y (Figura) son equivalentes porque cualquier trazado cerrado es la suma de dos trazados: el primero va de A a B, y el segundo va de B a A. El trabajo realizado yendo a lo largo de un camino de B a A es el negativo del trabajo realizado yendo a lo largo del mismo camino de A a B, donde A y B son dos puntos cualesquiera en el camino cerrado:
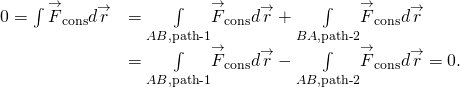
Usted podría preguntarse cómo vamos a probar si una fuerza es conservadora o no, ya que las definiciones involucran todos y cada uno de los caminos de A a B, o todos y cada uno de los caminos cerrados, pero para hacer la integral para el trabajo, tiene que elegir un camino en particular. Una respuesta es que el trabajo realizado es independiente del camino si el trabajo infinitesimal
![]()
es un diferencial exacto, la forma en que el trabajo neto infinitesimal era igual al diferencial exacto de la energía cinética,
![]()
cuando derivamos el teorema de energía de trabajo en el Teorema de Energía de Trabajo. Hay condiciones matemáticas que se pueden usar para probar si el trabajo infinitesimal realizado por una fuerza es un diferencial exacto, y la fuerza es conservadora. Estas condiciones solo implican diferenciación y, por lo tanto, son relativamente fáciles de aplicar. En dos dimensiones, la condición para
![]()
ser un diferencial exacto es
![]()
Usted puede recordar que el trabajo realizado por la fuerza en (Figura) dependía del camino. Para que la fuerza,
![]()
por lo Tanto,
![]()
lo que indica que no es una fuerza conservadora. ¿Puedes ver lo que podrías cambiar para convertirlo en una fuerza conservadora?

Ejemplo
Conservador o No?
¿Cuáles de las siguientes fuerzas bidimensionales son conservadoras y cuáles no? Supongamos que a y b son constantes con unidades apropiadas:
(a)
![]()
(b)
![]()
(c)
![]()
Estrategia
Aplique la condición indicada en (Figura), a saber, utilizando las derivadas de los componentes de cada fuerza indicada. Si la derivada del componente y de la fuerza con respecto a x es igual a la derivada del componente x de la fuerza con respecto a y, la fuerza es una fuerza conservadora, lo que significa que el camino tomado para los cálculos de energía potencial o trabajo siempre produce los mismos resultados.
Solución
-
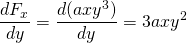
y
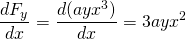
, de modo que esta fuerza no es conservador.
-
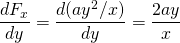
y
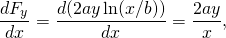
de modo que esta fuerza es conservador.
-
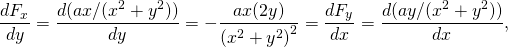
de nuevo conservador.
Significancia
Las condiciones en (Figura) son derivadas como funciones de una sola variable; en tres dimensiones, existen condiciones similares que involucran más derivadas.
Compruebe Su Comprensión
Una fuerza conservadora bidimensional es cero en los ejes x e y, y satisface la condición
![]()
. ¿Cuál es la magnitud de la fuerza en el punto
![]()
Mostrar Solución
2.83 N
Antes de salir de esta sección, observamos que las fuerzas no conservadoras no tienen energía potencial asociada a ellas porque la energía se pierde en el sistema y no se puede convertir en trabajo útil más tarde. Así que siempre hay una fuerza conservadora asociada con cada energía potencial. Hemos visto que la energía potencial se define en relación con el trabajo realizado por las fuerzas conservadoras. Esa relación, (Figura), implicaba una integral para el trabajo; comenzando con la fuerza y el desplazamiento, se integraba para obtener el trabajo y el cambio en la energía potencial. Sin embargo, la integración es la operación inversa de la diferenciación; igualmente podrías haber comenzado con la energía potencial y haber tomado su derivada, con respecto al desplazamiento, para obtener la fuerza. El incremento infinitesimal de energía potencial es el producto escalar de la fuerza y el desplazamiento infinitesimal,
![]()
Aquí, hemos elegido para representar el desplazamiento en una dirección arbitraria, por
![]()
para no restringirse a cualquier particular coordinar dirección. También expresó el producto escalar en términos de la magnitud del desplazamiento infinitesimal y la componente de la fuerza en su dirección. Ambas cantidades son escalares, por lo que puede dividir por dl para obtener
![]()
Esta ecuación da la relación entre la fuerza y la energía potencial asociada a ella. En palabras, el componente de una fuerza conservadora, en una dirección particular, es igual al negativo de la derivada de la energía potencial correspondiente, con respecto a un desplazamiento en esa dirección. Para el movimiento unidimensional, digamos a lo largo del eje x, (Figura) da la fuerza vectorial completa,
![]()
En dos dimensiones,
![]()
A partir de esta ecuación, se puede ver por qué (Figura) es la condición para que el trabajo sea un diferencial exacto, en términos de las derivadas de los componentes de la fuerza. En general, se utiliza una notación derivada parcial. Si una función tiene muchas variables, la derivada se toma solo de la variable especificada por la derivada parcial. Las otras variables se mantienen constantes. En tres dimensiones, se agrega otro término para el componente z, y el resultado es que la fuerza es el negativo del gradiente de la energía potencial. Sin embargo, todavía no veremos ejemplos tridimensionales.
Ejemplo
Fuerza debida a una Energía Potencial Cuártica
La energía potencial para una partícula que experimenta un movimiento unidimensional a lo largo del eje x es
![]()
donde
![]()
Su energía total en
![]()
y no está sujeta a ninguna fuerza no conservadora. Encuentre (a) las posiciones donde su energía cinética es cero y (b) las fuerzas en esas posiciones.
Estrategia
(a) Podemos encontrar las posiciones donde
![]()
así que la energía potencial es igual a la energía total del sistema dado. (b) Usando (Figura), podemos encontrar la fuerza evaluada en las posiciones encontradas de la parte anterior, ya que la energía mecánica se conserva.
Solución
- La energía total del sistema de 2 J es igual a la energía elástica cuártica como se indica en el problema,

Resolviendo para
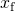
resultados en
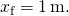
- De (Figura),
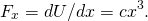
Por lo tanto, evaluar la fuerza en
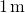
, tenemos
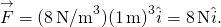
En ambas posiciones, la magnitud de las fuerzas es de 8 N y las direcciones son hacia el origen, ya que este es el potencial energía para una fuerza restauradora.
Significancia
Encontrar la fuerza de la energía potencial es matemáticamente más fácil que encontrar la energía potencial de la fuerza, porque diferenciar una función es generalmente más fácil que integrar una.
Compruebe Su Comprensión
Encuentra las fuerzas en la partícula en (Figura) cuando su energía cinética es 1.0 J at
![]()
Mostrar Solución
![]()
dirigido hacia el origen
Resumen
- Una fuerza conservadora es aquella para la que el trabajo realizado es independiente de la trayectoria. De manera equivalente, una fuerza es conservadora si el trabajo realizado sobre cualquier camino cerrado es cero.
- Una fuerza no conservadora es aquella para la que el trabajo realizado depende de la trayectoria.
- Para una fuerza conservadora, el trabajo infinitesimal es un diferencial exacto. Esto implica condiciones en las derivadas de los componentes de la fuerza.
- El componente de una fuerza conservadora, en una dirección particular, es igual al negativo de la derivada de la energía potencial para esa fuerza, con respecto a un desplazamiento en esa dirección.
Cuestiones Conceptuales
¿Cuál es el significado físico de una fuerza no conservadora?
Mostrar Solución
Una fuerza que quita energía del sistema que no se puede recuperar si invertimos la acción.
Una botella de cohetes se dispararon hacia arriba en el aire con una velocidad de
![]()
. Si se ignora la resistencia del aire, la botella subiría a una altura de aproximadamente
![]()
. Sin embargo, el cohete va hasta solo
![]()
antes de regresar al suelo. ¿Qué ha ocurrido? Explique, dando solo una respuesta cualitativa.
Una fuerza externa actúa sobre una partícula durante un viaje de un punto a otro y de regreso a ese mismo punto. Esta partícula solo es afectada por fuerzas conservadoras. ¿Cambia la energía cinética y la energía potencial de esta partícula como resultado de este viaje?
Mostrar Solución
El cambio en la energía cinética es el trabajo en red. Dado que las fuerzas conservadoras son independientes del camino, cuando están de vuelta al mismo punto, las energías cinéticas y potenciales son exactamente las mismas que al principio. Durante el viaje se conserva la energía total, pero tanto la energía potencial como la cinética cambian.
Problemas
Una fuerza
![]()
actúa sobre la partícula cuando se mueve a lo largo del eje x positivo. (a) Cuánto trabajo hace la fuerza sobre la partícula a medida que se mueve desde
![]()
to
![]()
(b) Elegir un punto de referencia conveniente de la energía potencial para ser cero en
![]()
encuentra la energía potencial para esta fuerza.
Una fuerza
![]()
actúa sobre una partícula. (a) Cuánto trabajo hace la fuerza sobre la partícula a medida que se mueve desde
![]()
to
![]()
(b) Elegir un punto de referencia conveniente de la energía potencial para ser cero en
![]()
encuentra la energía potencial para esta fuerza.
Mostrar Solución
![]()
Encontrar la fuerza correspondiente a la energía potencial
![]()
La energía potencial en función de uno de los dos átomos en una molécula diatómica es a menudo de forma aproximada
![]()
donde x es la distancia entre los átomos. (a) ¿A qué distancia de separación tiene la energía potencial un mínimo local (no al
![]()
(b) ¿Cuál es la fuerza en un átomo en esta separación? c) ¿Cómo varía la fuerza con la distancia de separación?
Mostrar Solución
un.
![]()
; b.
![]()
; c.
![]()
Una partícula de masa
![]()
se mueve bajo la influencia de la fuerza
![]()
Si su velocidad en
![]()
es
![]()
¿cuál es su velocidad en
![]()
Una partícula de masa
![]()
se mueve bajo la influencia de la fuerza
![]()
Si su velocidad en
![]()
es
![]()
¿cuál es su velocidad en
![]()
Mostrar Solución
![]()
Una caja con rodillos se empuja sin pérdida de energía por fricción a través del piso de un vagón de carga (consulte la siguiente figura). El coche se mueve a la derecha con una velocidad constante
![]()
Si la caja comienza en reposo en relación con el vagón de carga, a continuación, a partir del teorema de energía de trabajo,
![]()
donde d, la distancia que se mueve la caja, y v, la velocidad de la caja, se miden en relación con el vagón de carga. a) A un observador en reposo junto a las vías, a qué distancia
![]()
¿se empuja la caja cuando se mueve la distancia d en el coche? (b) Cuáles son las velocidades inicial y final de la caja
![]()
y
![]()
¿medido por el observador al lado de las vías? c) Demostrar que
![]()
y, en consecuencia, ese trabajo es igual al cambio en la energía cinética en ambos sistemas de referencia.

Glosario
fuerza conservadora la fuerza que funciona independientemente de la trayectoria diferencial exacta es la diferencia total de una función y requiere el uso de derivadas parciales si la función involucra más de una dimensión fuerza no conservadora la fuerza que funciona depende de la trayectoria
Leave a Reply